湖南省长沙市雨花区2022-2023学年九年级下学期数学假期开学考试测试卷
试卷更新日期:2023-02-14 类型:开学考试
一、选择题(共36分)
-
1. 在下列各数中,有理数是( )A、-5 B、 C、 D、π2. 下列计算正确的是( )A、5a2-3a2=2 B、(-2a2)3=-6a6 C、a3÷a=a2 D、(a+b)2=a2+b23. 下列四个图案中,不是中心对称图案的是( )A、
 B、
B、 C、
C、 D、
D、 4. 中新社北京1月27日电中国国家卫生健康委员会副主任曾益新27日在北京称,截至1月26日,中国已完成2276.7万剂次新冠疫苗接种.这里数据2276.7万可以用科学记数法表示为( )A、0.22767×107 B、2.2767×105 C、2.2767×107 D、2.2767×1065. 《九章算术》总共收集了246个数学问题,这些算法要比欧洲同类算法早1500多年,对中国及世界数学发展产生过重要影响.在《九章算术》中有很多名题,下面就是其中的一道.原文:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:如图,CD为⊙O的直径,弦AB⊥CD于点E.CE=1寸,AB=10寸,则可得直径CD的长为( )
4. 中新社北京1月27日电中国国家卫生健康委员会副主任曾益新27日在北京称,截至1月26日,中国已完成2276.7万剂次新冠疫苗接种.这里数据2276.7万可以用科学记数法表示为( )A、0.22767×107 B、2.2767×105 C、2.2767×107 D、2.2767×1065. 《九章算术》总共收集了246个数学问题,这些算法要比欧洲同类算法早1500多年,对中国及世界数学发展产生过重要影响.在《九章算术》中有很多名题,下面就是其中的一道.原文:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:如图,CD为⊙O的直径,弦AB⊥CD于点E.CE=1寸,AB=10寸,则可得直径CD的长为( )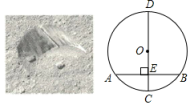 A、13寸 B、26寸 C、18寸 D、24寸6. 如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=6,∠C=30°,则△ACD的面积为( )
A、13寸 B、26寸 C、18寸 D、24寸6. 如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=6,∠C=30°,则△ACD的面积为( )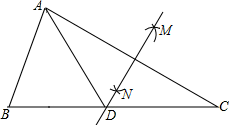 A、 B、 C、 D、97. 下列几何体中,主视图与俯视图不相同的是( )A、
A、 B、 C、 D、97. 下列几何体中,主视图与俯视图不相同的是( )A、 B、
B、 C、
C、 D、
D、 8. 一个多边形的每个内角均为120°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、八边形9. 不等式组的解集在数轴上用阴影表示正确的是( )A、
8. 一个多边形的每个内角均为120°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、八边形9. 不等式组的解集在数轴上用阴影表示正确的是( )A、 B、
B、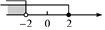 C、
C、 D、
D、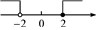 10. 中国总理李克强2020年6月1日考察山东时表示,地摊经济、小店经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机.市场、企业、个体工商户活起来,生存下去,再发展起来,国家才能更好!为了响应党中央、国务院的号召,各地有序开放了“地摊经济”、“马路经济”,长沙某地摊摊主将进价为10元的小商品提价100%后再6折销售,该小商品的利润率( )A、40% B、20% C、60% D、30%11. 如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是( )
10. 中国总理李克强2020年6月1日考察山东时表示,地摊经济、小店经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机.市场、企业、个体工商户活起来,生存下去,再发展起来,国家才能更好!为了响应党中央、国务院的号召,各地有序开放了“地摊经济”、“马路经济”,长沙某地摊摊主将进价为10元的小商品提价100%后再6折销售,该小商品的利润率( )A、40% B、20% C、60% D、30%11. 如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是( )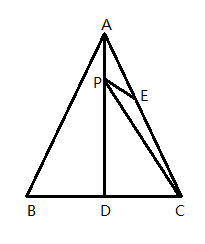 A、30° B、45° C、60° D、90°12. 如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M、N.下列结论:①BE+DF=EF;②AF平分∠DFE;③AM•AE=AN•AF;④AB2=BN•DM.其中正确的结论是( )
A、30° B、45° C、60° D、90°12. 如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M、N.下列结论:①BE+DF=EF;②AF平分∠DFE;③AM•AE=AN•AF;④AB2=BN•DM.其中正确的结论是( )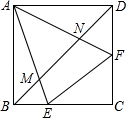 A、②③④ B、①④ C、①②③ D、①②③④
A、②③④ B、①④ C、①②③ D、①②③④二、填空题(共12分)
-
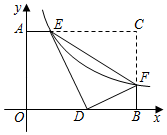
13. 分解因式:4a2b-b= .14. 若圆锥的底面直径为6cm,母线长为10cm,则圆锥的侧面积为cm2 .15. 一元二次方程x2-2x-k=0有两个相等的实数根,则k= .16. 如图,已知,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=(k>0)的图象与AC边交于点E,将△CEF沿EF对折后,C点恰好落在OB上的点D处,则k的值为 .
三、解答题(共72分)
-
17. 计算:( )﹣1﹣2cos30°+ +(3﹣π)018. 先化简,再求值: , 其中a= .19. 某校组织代表队参加市“与经典同行”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分).A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100,并绘制如下两幅不完整的统计图:请根据图中信息,解答下列问题:
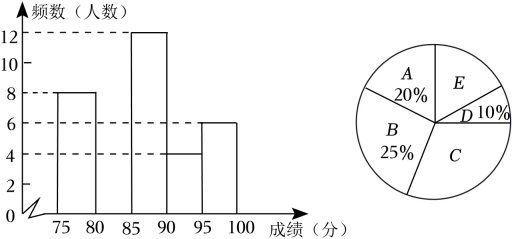 (1)、参加初赛的选手共有 名,请补全频数分布直方图;(2)、扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?(3)、学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中两名女生的概率.20. 如图,E是正方形ABCD对角线BD上一点,连接AE,CE,并延长CE交AD于点F.
(1)、参加初赛的选手共有 名,请补全频数分布直方图;(2)、扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?(3)、学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中两名女生的概率.20. 如图,E是正方形ABCD对角线BD上一点,连接AE,CE,并延长CE交AD于点F.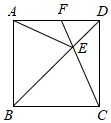 (1)、求证:△ABE≌△CBE;(2)、若∠AEC=140°,求∠DFE的度数.21. 为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行.
(1)、求证:△ABE≌△CBE;(2)、若∠AEC=140°,求∠DFE的度数.21. 为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行. (1)、求点F到直线CE的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).22. 某体育用品店准备购进甲,乙品牌乒乓球两种,若购进甲种乒乓球10个,乙种乒乓球5个,需要100元,若购进甲种乒乓球5个,乙种乒乓球3个,需要55元.(1)、求购进甲,乙两种乒乓球每个各需多少元?(2)、若该体育用品店刚好用了1000元购进这两种乒乓球,考虑顾客需求,要求购进甲种乒乓球的数量不少于乙种乒乓球数量的6倍,且乙种乒乓球数量不少于23个,那么该文具店共有哪几种进货方案?(3)、若该体育用品店销售每只甲种乒乓球可获利润3元,销售每只乙种乒乓球可获利润4元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?23. 如图,AB为⊙O的直径,C为⊙O上一点,D是弧BC的中点,BC与AD、OD分别交于点E、F.
(1)、求点F到直线CE的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).22. 某体育用品店准备购进甲,乙品牌乒乓球两种,若购进甲种乒乓球10个,乙种乒乓球5个,需要100元,若购进甲种乒乓球5个,乙种乒乓球3个,需要55元.(1)、求购进甲,乙两种乒乓球每个各需多少元?(2)、若该体育用品店刚好用了1000元购进这两种乒乓球,考虑顾客需求,要求购进甲种乒乓球的数量不少于乙种乒乓球数量的6倍,且乙种乒乓球数量不少于23个,那么该文具店共有哪几种进货方案?(3)、若该体育用品店销售每只甲种乒乓球可获利润3元,销售每只乙种乒乓球可获利润4元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?23. 如图,AB为⊙O的直径,C为⊙O上一点,D是弧BC的中点,BC与AD、OD分别交于点E、F.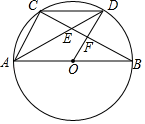 (1)、求证:DO∥AC;(2)、求证:DE•DA=DC2;(3)、若tan∠CAD= , 求sin∠CDA的值.24. 定义:在平面直角坐标系中,点P(x,y)的横、纵坐标的绝对值之和叫做点P(x,y)的勾股值,记[P]=|x|+|y|.(1)、已知M(p,2p)在反比例函数y=的图象上,且[M]=3,求反比例函数的解析式;(2)、已知点A是直线y=x+2上的点,且[A]=4,求点A的坐标;(3)、若抛物线y=ax2+bx+1与直线y=x只有一个交点C,已知点C在第一象限,且2≤[C]≤4,令t=2b2-4a+2020,求t的取值范围.25. 如图,在平面直角坐标系中,抛物线(a<0)与x轴交于A(-2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)、求证:DO∥AC;(2)、求证:DE•DA=DC2;(3)、若tan∠CAD= , 求sin∠CDA的值.24. 定义:在平面直角坐标系中,点P(x,y)的横、纵坐标的绝对值之和叫做点P(x,y)的勾股值,记[P]=|x|+|y|.(1)、已知M(p,2p)在反比例函数y=的图象上,且[M]=3,求反比例函数的解析式;(2)、已知点A是直线y=x+2上的点,且[A]=4,求点A的坐标;(3)、若抛物线y=ax2+bx+1与直线y=x只有一个交点C,已知点C在第一象限,且2≤[C]≤4,令t=2b2-4a+2020,求t的取值范围.25. 如图,在平面直角坐标系中,抛物线(a<0)与x轴交于A(-2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.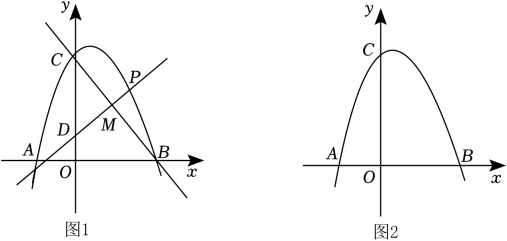 (1)、试求抛物线的解析式;(2)、直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m= , 试求m的最大值及此时点P的坐标:(3)、连接AC,抛物线上是否存在点Q,使得∠BAQ=2∠OCA?如果存在,请求出点Q的坐标;如果不存在,请说明理由.
(1)、试求抛物线的解析式;(2)、直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m= , 试求m的最大值及此时点P的坐标:(3)、连接AC,抛物线上是否存在点Q,使得∠BAQ=2∠OCA?如果存在,请求出点Q的坐标;如果不存在,请说明理由.