贵州省遵义市余庆县2022-2023学年七年级上学期期末数学试卷

试卷更新日期：2023-02-14 类型：期末考试

进入出卷网下载

一、选择题（本题共12小题，共48分）

1. 某商场要检测4颗的质量，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数，从质量角度看，最接近标准的是（）

A、 B、 C、 D、

查看试题解析
2. 2021年2月10日19时52分，中国首次火星探测任务“天问一号”探测器成功“刹车”被火星“捕获”．在制动捕获过程中，探测器距离地球的距离为192000000公里．数字192000000用科学记数法表示为（）

A、 19.2×10⁷ B、19.2×10⁸ C、1.92×10⁸ D、1.92×10⁹

查看试题解析
3. 已知一个单项式的系数为-3，次数为4，这个单项式可以是（）

A、 $3 x y$ B、 $3 x^{2} y^{2}$ C、 $- 3 x^{2} y^{2}$ D、 $4 x^{3}$

查看试题解析
4. 下列方程中，解为 $x = 2$ 的是（）

A、 $2 x = 6$ B、 $(x - 3) (x + 2) = 0$ C、 $x^{2} = 3$ D、 $3 x - 6 = 0$

查看试题解析
5. 下列各式错误的是（）

A、 $- 4 > - 5$ B、 $- (- 3) = 3$ C、 $- | - 4 | = 4$ D、 $16 \div (- 4)^{2} = 1$

查看试题解析
6. 如图所示，几何体由6个大小相同的立方体组成，其俯视图是（）

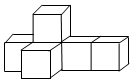A、 B、 C、 D、

查看试题解析
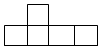7. 下列计算正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $5 a b^{2} - 5 a^{2} b = 0$ C、 $7 a + a = 7 a^{2}$ D、 $- a b + 3 b a = 2 a b$

查看试题解析
8. 如图，在不完整的数轴上有A ， B两点，它们所表示的两个有理数互为相反数，则关于原点位置的描述正确的是（　　）

A、在点A的左侧 B、与线段AB 的中点重合 C、在点B的右侧 D、与点A或点B重合

查看试题解析
9. 下列方程变形中，正确的是（）

A、方程 $\frac{x - 1}{2} - \frac{x}{5} = 1$ ，去分母得 $5 (x - 1) - 2 x = 10$ B、方程 $3 - x = 2 - 5 (x - 1)$ ，去括号得 $3 - x = 2 - 5 x - 1$ C、方程 $\frac{2}{3} t = \frac{3}{2}$ ，系数化为 $1$ 得 $t = 1$ D、方程 $3 x - 2 = 2 x + 1$ ，移项得 $3 x - 2 x = - 1 + 2$

查看试题解析
10. 下面是两位同学的对话，根据对话内容，可求出这位同学的年龄是（）

A、11岁 B、12岁 C、13岁 D、14岁

查看试题解析
11. 如图， $A B = 12 c m$ ， $C$ 为 $A B$ 的中点，点 $D$ 在线段 $A C$ 上，且 $C D$ ： $C B = 2$ ： $3$ ，则 $D B$ 的长度为（）

A、 $4 c m$ B、 $6 c m$ C、 $8 c m$ D、 $10 c m$

查看试题解析
12. 将边长为1的正方形纸片如图1所示的方法进行对折，记第一次对折后得到的图形面积为 $S_{1}$ ，第2次对折后得到的图形面积为 $S_{2} \dots$ ，第 $n$ 次对折后得到的图形面积为 $S_{n}$ ，请根据图2化简 $S_{1} + S_{2} + S_{3} \dots S_{2014} =$ （）

A、 $1 - \frac{1}{2^{2015}}$ B、 $\frac{2014}{2015}$ C、 $1 - \frac{1}{2^{2014}}$ D、 $\frac{2013}{2014}$

查看试题解析

二、填空题（本题共4小题，共16分）

13. 在1，0，-2，-1这四个数中，最小的数是．

查看试题解析
14. 如图，射线 $O A$ 的方向是北偏东 $26 ° 38'$ ，那么 $∠ α =$ ．

查看试题解析
15. 用代数式表示“ $a$ 的两倍与 $b$ 的平方的和”：．

查看试题解析
16. 定义：对于任意两个有理数 $a$ ， $b$ ，可以组成一个有理数对 $(a ， b)$ ，我们规定 $(a ， b) = a + b - 1 .$ 例如 $(- 2 ， 5) = - 2 + 5 - 1 = 2$ ．
根据上述规定解决下列问题：

(1)、有理数对 $(2 ， - 1) =$ ；

(2)、当满足等式 $(- 5 ， 3 x + 2 m) = 5$ 的 $x$ 是正整数时，则 $m$ 的正整数值为．

查看试题解析

三、解答题（本题共8小题，共86分）

17. 计算：

(1)、 $- \frac{3}{4} \times (12 - \frac{2}{3})$ ；

(2)、 $- 2^{4} + | - 5 | - [- (- 3) \div \frac{1}{6} + 2]$ ．

查看试题解析
18. 解方程：

(1)、 $2 x - 3 = 4 (x - 1)$ ；

(2)、 $\frac{3 x - 5}{6} - \frac{x - 2}{3} = 1$ ．

查看试题解析
19. 小明化简 $(4 a^{2} - 2 a - 6) - 2 (2 a^{2} - 2 a - 5)$ 的过程如下，请指出他化简过程中的错误，写出对应的序号，并写出正确的化简过程：
解： $(4 a^{2} - 2 a - 6) - 2 (2 a^{2} - 2 a - 5)$
$= 4 a^{2} - 2 a - 6 - 4 a^{2} + 4 a + 5 ①$
$= (4 - 4) a^{2} + (- 2 + 4) a + (- 6 + 5) ②$
$= 2 a - 1 ③$
他化简过程中出错的是第 ▲ 步 $($ 填序号 $)$ ；
正确的解答是：

查看试题解析
20. 请用下列工具按要求画图，并标出相应的字母．
已知：点 $P$ 在直线 $a$ 上，点 $Q$ 在直线 $a$ 外．
⑴画线段 $P Q$ ；
⑵画线段 $P Q$ 的中点 $M$ ；
⑶画直线 $b$ ，使 $b ⊥ P Q$ 于点 $M$ ；
⑷直线 $b$ 与直线 $a$ 交于点 $N$ ；
⑸利用半圆仪测量出 $∠ P N M \approx$ ▲ $° ($ 精确到 $1 °)$ ．

查看试题解析
21. 2019年2月，市城区公交车施行全程免费乘坐政策，标志着我市公共交通建设迈进了一个新的时代．如图为某一条东西方向直线上的公交线路，东起职教园区站，西至富士康站，途中共设12个上下车站点，如图所示：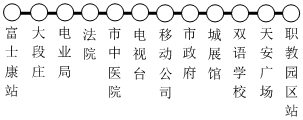

某天，小王从电业局站出发，始终在该线路的公交站点做志愿者服务，到 $A$ 站下车时，本次志愿者服务活动结束，如果规定向东为正，向西为负，当天的乘车站数按先后顺序依次记录如下 $($ 单位：站 $)$ ：+5，-2，+6，-11，+8﹐+1，-3，-2，-4，+7

(1)、请通过计算说明 $A$ 站是哪一站？

(2)、若相邻两站之间的平均距离为1.2千米，求这次小王志愿服务期间乘坐公交车行进的总路程是多少千米？

查看试题解析
22. 如图是一个长方形游乐场，其宽是 $4 a$ 米，长是 $6 a$ 米．其中半圆形休息区和长方形游泳区以外的地方都是绿地．已知半圆形休息区的直径和长方形游泳区的宽是 $2 a$ 米，游泳区的长是 $3 a$ 米．

(1)、该游乐场休息区的面积为 $m^{2}$ ，游泳区的面积为 $m^{2} . ($ 用含有 $a$ 的式子表示 $)$

(2)、若长方形游乐场的宽为40米，绿化草地每平方米需要费用30元，求这个游乐场中绿化草地的费用．

查看试题解析
23. 阅读材料并回答问题：
数学课上，老师提出了如下问题：

已知点 $O$ 在直线 $A B$ 上， $∠ C O E = 90 °$ ，在同一平面内，过点 $O$ 作射线 $O D$ ，满足 $∠ A O C = 2 ∠ A O D .$ 当 $∠ B O C = 40 °$ 时，如图1所示，求 $∠ D O E$ 的度数．

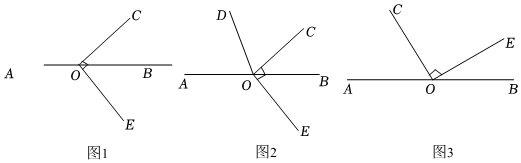
甲同学：以下是我的解答过程 $($ 部分空缺 $)$

解：如图2， $∵$ 点 $O$ 在直线 $A B$ 上，

$∴ ∠ A O B = 180 °$ ．

$∵ ∠ B O C = 40 °$ ，

$∴ ∠ A O C =$       ▲       $° .$

$∵ ∠ A O C = 2 ∠ A O D$ ，

$∴ O D$ 平分 $∠ A O C$ ．

$∴ ∠ C O D = \frac{1}{2} ∠ A O C =$       ▲       $° .$

$∵ ∠ D O E = ∠ C O D + ∠ C O E$ ， $∠ C O E = 90 °$ ，

$∴ ∠ D O E =$       ▲       $° .$

乙同学：“我认为还有一种情况．”

请完成以下问题：

(1)、请将甲同学解答过程中空缺的部分补充完整．

(2)、判断乙同学的说法是否正确，若正确，请在图1中画出另一种情况对应的图形，并求 $∠ D O E$ 的度数，写出解答过程；若不正确，请说明理由．

(3)、将题目中“ $∠ B O C = 40 °$ ”的条件改成“ $∠ B O C = α$ ”，其余条件不变，当 $α$ 在 $90 °$ 到 $180 °$ 之间变化时，如图.所示， $α$ 为何值时， $∠ C O D = ∠ B O E$ 成立？请直接写出此时 $α$ 的值．

查看试题解析
24. 为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费．下表是该市民“一户一表“生活用水阶梯式计费价格表的部分信息：
自来水销售价格
污水处理价格
每户每月用水量
单价：元 $/$ 吨
单价：元 $/$ 吨
17吨及以下
$a$
0.90
超过17吨但不超过30吨的部分
$b$
0.90
超过30吨的部分
6.00
0.90
$($ 说明：每户生产的污水量等于该户自来水用量； $②$ 水费 $=$ 自来水费用 $+$ 污水处理费 $)$
已知小王家2018年7月用水16吨，交水费43.2元.8月份用水25吨，交水费75.5元．

(1)、求 $a$ 、 $b$ 的值；

(2)、如果小王家9月份上交水费156.1元，则小王家这个月用水多少吨？

(3)、小王家10月份忘记了去交水费，当他11月去交水费时发现两个月一共用水50吨，其中10月份用水超过30吨，一共交水费215.8元，其中包含30元滞纳金，求小王家11月份用水多少吨？ $($ 滞纳金：因未能按期缴纳水费，逾期要缴纳的“罚款金额” $)$

查看试题解析

自来水销售价格		污水处理价格
每户每月用水量	单价：元 $/$ 吨	单价：元 $/$ 吨
17吨及以下	$a$	0.90
超过17吨但不超过30吨的部分	$b$	0.90
超过30吨的部分	6.00	0.90