浙江省宁波市鄞州区4校联考2022-2023学年九年级上学期期末考试数学试题

试卷更新日期：2023-02-14 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $\frac{a}{b} = \frac{2}{3}$ ，则下列说法错误的是（）

A、 $\frac{a + b}{b} = \frac{5}{3}$ B、 $\frac{a}{b} = \frac{a + 2}{b + 3}$ C、 $2 a = 3 b$ D、 $\frac{a}{2} = \frac{b}{3}$

查看试题解析
2. 某水果超市为了吸引顾客来店购物，设立了一个如图所示的可以自由转动的转盘，开展有奖购物活动.顾客购买商品满200元就能获得一次转动转盘的机会，当转盘停止时，指针落在“一袋苹果”的区域就可以获得一袋苹果；指针落在“一袋橘子”的区域就可以获得一袋橘子.若转动转盘2000次，指针落在“一袋橘子”区域的次数有600次，则某位顾客转动转盘一次，获得一袋橘子的概率大约是（）

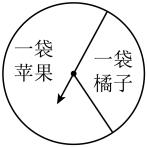A、0.3 B、0.7 C、0.4 D、0.2

查看试题解析
3. 如图，在4×4正方形网格中，点A、B、C为网格交点，AD⊥BC，垂足为D，则sin∠BAD的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
4. 如图， $A B$ 是 $⊙ O$ 的直径，点D在 $A B$ 的延长线上， $D C$ 切 $⊙ O$ 于点C，若 $∠ A = 26 °$ ，则 $∠ D$ 等于（）

A、 $26 °$ B、 $48 °$ C、 $38 °$ D、 $52 °$

查看试题解析
5. 点A（m-1，y₁），B（m，y₂）都在二次函数y=（x-1）²+n的图象上.若y₁＜y₂ ，则m的取值范围为（）

A、 $m > 2$ B、 $m > \frac{3}{2}$ C、 $m < 1$ D、 $\frac{3}{2} < m < 2$

查看试题解析
6. 如图，在平面直角坐标系中，已知 $A (1 ， 0)$ ， $B (2 ， 1)$ ， $D (3 ， 0)$ ， $△$ ABC与 $△$ DEF位似，原点O是位似中心，则E点的坐标是（）

A、 $(7 ， 4)$ B、 $(7 ， 3)$ C、 $(6 ， 4)$ D、 $(6 ， 3)$

查看试题解析
7. 如图，扇形 $A O B$ 圆心角为直角， $O A = 10$ ，点C在 $\overset{⌢}{A B}$ 上，以 $O A$ ， $C A$ 为邻边构造 $▱ A C D O$ ，边 $C D$ 交 $O B$ 于点E，若 $O E = 8$ ，则图中两块阴影部分的面积和为（　　）

A、 $10 π - 8$ B、 $5 π - 8$ C、 $25 π - 64$ D、 $50 π - 64$

查看试题解析
8. 如图，PA、PB是⊙O的切线，A、B是切点，点C在⊙O上，且 $∠ A C B = 58 °$ ，则 $∠ A P B$ 等于（）

A、 $54 °$ B、 $56 °$ C、 $64 °$ D、 $68 °$

查看试题解析
9. 如图，已知菱形 $A B C D$ 的边长为4，对角线 $A C 、 B D$ 相交于点O，点 $M 、 N$ 分别是边 $B C 、 C D$ 上的动点， $∠ B A C = ∠ M A N = 60 °$ ，连接 $M N 、 O M$ ， $M N$ 与 $A C$ 相交于点E．以下四个结论：① $△ A M N$ 点是等边三角形；② $M N$ 的最小值是 $2 \sqrt{3}$ ；③若 $B M = 3$ 时， $C E = \frac{3}{4}$ ；④当 $O M ⊥ B C$ 时， $O A^{2} = D N · A B$ ．其中正确的个数有（）

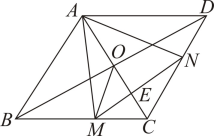A、1个 B、2个 C、3个 D、4

查看试题解析
10. 如图，E，F，G，H分别是矩形 $A B C D$ 四条边上的点，连接 $E F ， G H$ 相交于点I，且 $G H ∥ A D$ ， $E F ∥ A B$ ，矩形 $B F I G ∽$ 矩形 $E I H D$ ，连接 $A C$ 交 $G H ， E F$ 于点P，Q，下列一定能求出 $△ D P Q$ 面积的条件是（）

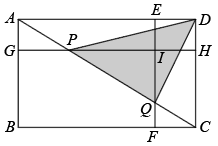A、矩形 $B F I G$ 和矩形 $E I H D$ 的面积之差 B、矩形 $A B C D$ 与矩形 $B F I G$ 的面积之差 C、矩形 $B F I G$ 和矩形 $F C H I$ 的面积之差 D、矩形 $B F I G$ 和矩形 $E I G A$ 的面积之差

查看试题解析

二、填空题

11. 抛物线 $y = - 3 (x - 1)^{2} + 2$ 的顶点坐标是．

查看试题解析
12. 若 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{3}{4}$ ，则 $\frac{a - 2 c + 3 e}{b - 2 d + 3 f} =$ .

查看试题解析
13. 当 $a \leq x \leq a + 1$ 时，函数 $y = x^{2} - 2 x + 1$ 的最小值为4，则a的值为.

查看试题解析
14. 如图，一副三角板如图1放置， $A B = C D = \sqrt{6}$ ，顶点 $E$ 重合，将 $△ D E C$ 绕其顶点 $E$ 旋转，如图2，在旋转过程中，当 $∠ A E D = 75 °$ ，连接 $A D$ ， $B C$ ，此时四边形 $A B C D$ 的面积是.

查看试题解析
15. 如图，四边形ABCD内接于以BD为直径的⊙O，CA平分∠BCD，若四边形ABCD的面积是30cm² ，则AC=cm.

查看试题解析
16. 如图1是一种利用镜面反射，放大微小变化的装置.木条BC上的点P处安装一平面镜，BC与刻度尺边MN的交点为D，从A点发出的光束经平面镜P反射后，在MN上形成一个光点E.已知 $A B ⊥ B C ， M N ⊥ B C ， A B = 6.5$ ， $B P = 4 ， P D = 8$ .

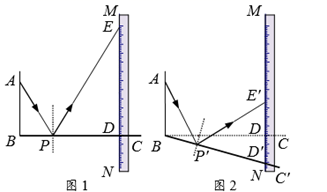(1)、ED的长为.

(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 $B C^{'}$ （如图2），点P的对应点为 $P^{'}$ ， $B C^{'}$ 与MN的交点为D′，从A点发出的光束经平面镜 $P^{'}$ 反射后，在MN上的光点为 $E^{'}$ .若 $D D^{'} = 5$ ，则 $E E^{'}$ 的长为.

查看试题解析

三、解答题

17. 计算：

(1)、 $6 t a n 30 ° - 2 t a n 45 ° s i n 60 °$ .

(2)、 $(\frac{1}{2})^{- 1} - (\sqrt{3} - 2)^{0} + 4 c o s 30 ° - \sqrt{12}$ .

查看试题解析
18. 第 24 届北京冬奥会开幕式二十四节气倒计时惊艳亮相，从“雨水”开始，一路倒数，最终行至“立春”，将中国人独有的浪漫传达给了全世界.李老师为了让学生深入了解二十四节气，将每个节气的名称写在完全相同且不透明的小卡片上，洗匀后将卡片倒扣在桌面上，邀请同学上讲台随机抽取一张卡片，并向大家介绍卡片上对应节气的含义.

(1)、若随机抽取一张卡片，则上面写有“立夏”的概率为？

(2)、李老师选出写有“立春、立夏、立秋、立冬”的四张卡片洗匀后倒扣在桌面上，请小丽同学从中抽取一张卡片记下节气名称，然后放回洗匀再随机抽取一张卡片记下节气名称.请利用画树状图或列表的方法，求两次抽到的卡片上写有相同节气名称的概率.

查看试题解析
19. 如图，在正方形网格中，△ABC的顶点都在小正方形的格点上.
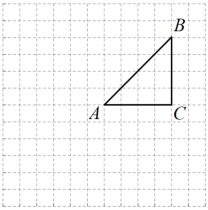
⑴请找出 $△ A B C$ 的外接圆的圆心O，并标明圆心O的位置；
⑵请以圆心O为位似中心，在点O的下方画出边 $A C$ 放大2倍后的线段 $P Q$ .

查看试题解析
20. 如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于E，连接AC，OC，BC．

(1)、求证：∠1=∠2；

(2)、若 $B E = 2 ， C D = 6$ ，求⊙O的半径的长．

查看试题解析
21. 某校安装了红外线体温检测仪（如图1），该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温，其红外线探测点 $O$ 可以在垂直于地面的支杆 $O P$ 上下调节（如图2），探测最大角（ $∠ O B C$ ）为58°，探测最小角（ $∠ O A C$ ）为26.6°，已知该设备在支杆 $O P$ 上下调节时，探测最大角及最小角始终保持不变.（结果精确到0.01米，参考数据： $s i n 58 ° \approx 0.85$ ， $c o s 58 ° \approx 0.53$ ， $t a n 58 ° \approx 1.60$ ， $s i n 26.6 ° \approx 0.45$ ， $c o s 26.6 ° \approx 0.89$ ， $t a n 26.6 ° \approx 0.50$ ）

(1)、若该设备的安装高度 $O C$ 为1.6米时，求测温区域的宽度 $A B$ ；

(2)、若要求测温区域的宽度 $A B$ 为2.53米，请你帮助学校确定该设备的安装高度 $O C$ .

查看试题解析
22. 某超市销售一种衬衫，平均每天可售出20件，每件盈利40元.为了扩大销售，加盈利，该超市准备适当降价，经过一段时间测算，发现每件衬衫每降低1元，平均每天可多售出2件.

(1)、若每件衬衫降价4元时，平均每天可售出多少件衬衫？此时每天销售获利多少元？

(2)、在每件盈利不少于25元的前提下，要使该衬衫每天销售获利为1200元，同每件衬衫应降价多少元？

(3)、该衬衫每天的销售获利能达到1300元吗？如果能，请写出降价方案，如果不能，请说明理由.

查看试题解析
23. 如图1，点E是四边形 $A B C D$ 的边 $B C$ 上一点，分别连接 $E A$ ， $E D$ ，把四边形 $A B C D$ 分成三个三角形，如果其中有两个三角形相似，那么我们把点E叫做四边形 $A B C D$ 的边 $B C$ 上的“相似点”；如果这三个三角形都相似，那么我们把点E叫做四边形 $A B C D$ 的边 $B C$ 上的“强相似点”.

(1)、任务一：如图1， $∠ B = ∠ C = ∠ A E D = α °$ ，试判断点E是否是四边形 $A B C D$ 的边 $B C$ 上的“相似点”，并说明理由；

(2)、任务二：如图2，矩形 $A B C D$ 的四个顶点A，B，C，D均在正方形网格的格点上，试在图中画出矩形 $A B C D$ 的边 $B C$ 上的“强相似点”；

(3)、任务三：如图3，矩形 $A B C D$ 中， $A B = 6$ ，将矩形 $A B C D$ 沿 $C E$ 折叠，点D落在 $A B$ 边上的点F处，若点F是四边形 $A B C E$ 的边 $A B$ 上“强相似点”，求 $B C$ .

查看试题解析
24. 如图，已知二次函数 $y = a x^{2} + b x + c$ 的图象与x轴交于A和 $B (3 ， 0)$ 两点，与y轴交于 $C (0 ， - 2)$ ，对称轴为直线 $x = \frac{5}{4}$ ，连接BC，在直线BC上有一动点P，过点P作y轴的平行线交二次函数的图象于点N，交x轴于点M，

(1)、求抛物线与直线BC的函数解析式；

(2)、设点M的坐标为 $(m ， 0)$ ，求当以PN为直径的圆与y轴相切时m的值：

(3)、若点P在线段BC上运动，则是否存在这样的点P，使得 $△ C P N$ 与 $△ B P M$ 相似，若存在请直接写出点P的坐标，若不存在，请写出理由.

查看试题解析