浙江省金华市义乌稠州教育集团2022-2023学年七年级上学期第二次独立作业检测数学试题
试卷更新日期:2023-02-14 类型:期末考试
一、单选题
-
1. 2022年即将离我们而去,的相反数是( )A、 B、 C、-2022 D、20222. 一周时间有604800秒,604800用科学记数法表示为( )A、 B、 C、 D、3. 现实生活中,总有人乱穿马路(如图中AD),却不愿从天桥(如图中 )通过,请用数学知识解释这一现象,其原因是( )
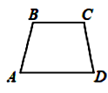 A、两点之间线段的长度,叫做这两点之间的距离 B、过一点有无数条直线 C、两点确定一条直线 D、两点之间,线段最短4. 如图,数轴上蚂蚁所在点表示的数可能为( )
A、两点之间线段的长度,叫做这两点之间的距离 B、过一点有无数条直线 C、两点确定一条直线 D、两点之间,线段最短4. 如图,数轴上蚂蚁所在点表示的数可能为( ) A、3 B、0 C、-1 D、-25. 等式就像平衡的天平,能与如图的事实具有相同性质的是( )
A、3 B、0 C、-1 D、-25. 等式就像平衡的天平,能与如图的事实具有相同性质的是( )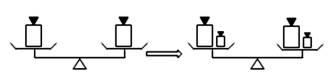 A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么6. 下列是无理数的是( )A、 B、 C、 D、3.147. 下列四个图中,能表示线段的是( )A、
A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么6. 下列是无理数的是( )A、 B、 C、 D、3.147. 下列四个图中,能表示线段的是( )A、 B、
B、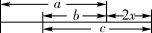 C、
C、 D、
D、 8. 根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是 , 若输入x的值是 , 则输出y的值是( )
8. 根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是 , 若输入x的值是 , 则输出y的值是( ) A、5 B、19 C、0 D、219. 福州某机械厂加工车间有35名工人,平均每名工人每天加工大齿轮5个或小齿轮10个,已知2个大齿轮和3个小齿轮配成一套,问分别安排多少名工人加工大、小齿轮,才能刚好配套?若设加工大齿轮的工人有x名,则可列方程为( )A、3×5x=2×10(35-x) B、2×5x=3×10(35-x) C、3×10x=2×5(35-x) D、2×10x=3×5(35-x)10. 把六张大小形状完全相同的小平行四边形卡片(如图)放在一个底面为平行四边形的盒子底部,两种放置方法如图2、图3所示,其中3中的重叠部分是平行四边形EFGH,若EH=2GH,且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为( )
A、5 B、19 C、0 D、219. 福州某机械厂加工车间有35名工人,平均每名工人每天加工大齿轮5个或小齿轮10个,已知2个大齿轮和3个小齿轮配成一套,问分别安排多少名工人加工大、小齿轮,才能刚好配套?若设加工大齿轮的工人有x名,则可列方程为( )A、3×5x=2×10(35-x) B、2×5x=3×10(35-x) C、3×10x=2×5(35-x) D、2×10x=3×5(35-x)10. 把六张大小形状完全相同的小平行四边形卡片(如图)放在一个底面为平行四边形的盒子底部,两种放置方法如图2、图3所示,其中3中的重叠部分是平行四边形EFGH,若EH=2GH,且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为( )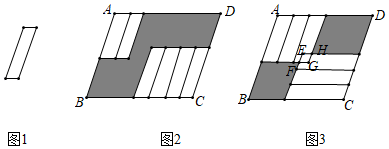 A、0.5 B、1 C、1.5 D、3
A、0.5 B、1 C、1.5 D、3二、填空题
-
11. 比较大小:-|-|-. (填“<”、“=”或“>”)12. 如果 与 的和仍是单项式,则 .13. 若x3=64,则 = .14. 如图,点C在线段AB上,且AC:BC=2:3,点D在线段AB的延长线上,且BD=AC,E为AD的中点,若AB=40cm,则线段CE=.
 15. 如图,在数轴上,点表示1,现将点沿数轴做如下移动,第一次将点向左移动3个单位长度到达点 , 第二次将点向右移动6个单位长度到达点 , 第三次将点向左移动9个单位长度到达点 , …按照这种移动规律进行下去,第101次移动到点 , 那么点所表示的数为.
15. 如图,在数轴上,点表示1,现将点沿数轴做如下移动,第一次将点向左移动3个单位长度到达点 , 第二次将点向右移动6个单位长度到达点 , 第三次将点向左移动9个单位长度到达点 , …按照这种移动规律进行下去,第101次移动到点 , 那么点所表示的数为. 16. 有一个长方体水箱,从里面量得它的深度为 , 底面长为 , 宽为 , 水箱里已盛有深度为的水.若往水箱里放入一个棱长为的立方体铁块,则水箱的水深为.
16. 有一个长方体水箱,从里面量得它的深度为 , 底面长为 , 宽为 , 水箱里已盛有深度为的水.若往水箱里放入一个棱长为的立方体铁块,则水箱的水深为.三、解答题
-
17. 计算(1)、(2)、18. 已知a、b满足(a+1)2+|2﹣b|=0.(1)、求a,b的值.(2)、若A=3a2﹣4ab,B=b2﹣2ab,求A﹣2B的值.19. 某工厂为满足市场需求计划每天生产600件防护服,如表是某一周的生产情况(超产部分记为正,减产部分记为负,单位:件).
星期
一
二
三
四
五
六
日
增减
+15
-12
+10
-15
-8
+15
+20
(1)、产量最多的一天比产量最少的一天多生产件;(2)、该工厂实行计件工资制,每生产一件支付工资20元,本周该工厂应支付工人的工资总额是多少元?20. 已知关于的方程:与有相同的解.(1)、求的值(2)、求以为未知数的方程的解.21. 已知2的平方等于a,2b-1是27的立方根,± 表示3的平方根.(1)、求a,b,c的值;(2)、化简关于x的多项式:|x-a|-2(x+b)-c,其中x<4.22. 已知为不相等的实数,且均不为 , 现定义有序实数对的“真诚值”为: , 如数对的“真诚值”为: , 数对的“真诚值”为:.(1)、根据上述的定义填空: , ;(2)、数对的“真诚值” , 求的值.23. 滴滴快车是一种便捷的出行工具,计费规则如表:计费项目
里程费
时长费
远途费
单价
1.8元/公里
0.3元/分钟
0.8元/公里
注:车费是里程费、时长费、远途费三部分之和,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里加收0.8元,不足1公里按1公里计算.
张敏与李良各自乘坐滴滴快车,到同一地点约见,已知到达约见地点时他们的实际行车里程分别为5公里与8公里.设张敏乘车时间为x分钟,李良乘车时间为y分钟.
(1)、则张敏乘车费为元(用含x的代数式表示),李良乘车费为元(用含y的代数式表示);(2)、若张敏比李良少支付2元钱,问张敏与李良的乘车时间哪个多?多几分钟?(3)、在(2)的条件下,已知乘车时间较少的人先到达约见地点等候,等候时间是他自己乘车时间的一半,且比另一人乘车时间的 少2分钟,问他俩谁先出发?先出发多少分钟?24. 如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3. (1)、数轴上点A表示的数为 .(2)、将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
(1)、数轴上点A表示的数为 .(2)、将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数为 ▲ .
②设点A的移动距离AA′=x.
ⅰ.当S=4时,x= ▲ ;
ⅱ.D为线段AA′的中点,点E在线段OO′上,且OE= OO′,当点D,E所表示的数互为相反数时,求x的值.