四川省成都市双流区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-14 类型:期末考试
一、单选题
-
1. 方程x2=4的解是( )A、x=2 B、x=-2 C、x=±2 D、没有实数根2. 如图,在矩形中,对角线 , 相交于点O,若 , 则的长为( )
 A、3 B、4 C、5 D、63. 反比例函数的图象在第( ).A、一、三象限 B、二、四象限 C、一、二象限 D、二、三象限4. 如图所示的几何体的俯视图是( )
A、3 B、4 C、5 D、63. 反比例函数的图象在第( ).A、一、三象限 B、二、四象限 C、一、二象限 D、二、三象限4. 如图所示的几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 我国南宋数学家杨辉所著的《田亩比类乘除算法》中有这样一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”意思是:一块矩形田地的面积为864平方步,只知道它的宽比长少12步,问它的长和宽各多少步?设这块田地的宽为x步,则所列的方程正确的是( )A、 B、 C、 D、6. 从一定的高度任意抛掷一枚质地均匀的硬币的次数很大时,落下后,正面朝上的频率最有可能接近的数值为( )A、0.53 B、0.87 C、1.03 D、1.057. 如图,已知和是以点O为位似中心的位似图形, , 的面积为4,则的面积为( )
5. 我国南宋数学家杨辉所著的《田亩比类乘除算法》中有这样一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”意思是:一块矩形田地的面积为864平方步,只知道它的宽比长少12步,问它的长和宽各多少步?设这块田地的宽为x步,则所列的方程正确的是( )A、 B、 C、 D、6. 从一定的高度任意抛掷一枚质地均匀的硬币的次数很大时,落下后,正面朝上的频率最有可能接近的数值为( )A、0.53 B、0.87 C、1.03 D、1.057. 如图,已知和是以点O为位似中心的位似图形, , 的面积为4,则的面积为( ) A、6 B、10 C、25 D、128. 如图,直线与x轴相交于点A , 与函数的图象交于点B,C,点B的横坐标是8,点C的横坐标是 , 则不等式组的解集是( )
A、6 B、10 C、25 D、128. 如图,直线与x轴相交于点A , 与函数的图象交于点B,C,点B的横坐标是8,点C的横坐标是 , 则不等式组的解集是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如果 , 那么 .10. 若点 , 都在反比例函数的图象上,则 , 的大小关系为:(填“>”或“<”).11. 如图, , , , 则.
 12. 已知关于x的一元二次方程有两个不相等的实数根,则实数k的取值范围是.13. 如图,菱形的对角线 , 相交于点 , 按下列步骤作图:
12. 已知关于x的一元二次方程有两个不相等的实数根,则实数k的取值范围是.13. 如图,菱形的对角线 , 相交于点 , 按下列步骤作图:①分别以点 , 为圆心,大于的长为半径画弧,两弧的交点分别为点 , ;
②过点 , 作直线 , 交于点;
③连接.若 , 则菱形的周长为.
 14. 已知 , 且 , 则的值为.15. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用,如图是小乐同学的健康码(绿码)示意图,用黑白打印机打印于边长为4cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 cm2.
14. 已知 , 且 , 则的值为.15. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用,如图是小乐同学的健康码(绿码)示意图,用黑白打印机打印于边长为4cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 cm2. 16. 若 , 是关于x的方程的两个实数根,则代数式的值是.17. 已知过原点的一条直线与反比例函数的图象交于 , 两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点 , 连接交轴于点.若 , 则.18. 如图,在和中, , E为的中点,将绕点O旋转,直线 , 交于点F,连接 , 则的最小值是.
16. 若 , 是关于x的方程的两个实数根,则代数式的值是.17. 已知过原点的一条直线与反比例函数的图象交于 , 两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点 , 连接交轴于点.若 , 则.18. 如图,在和中, , E为的中点,将绕点O旋转,直线 , 交于点F,连接 , 则的最小值是.
三、解答题
-
19.(1)、计算:(2)、解方程:.20. 某小队在探险过程途中发现一个深坑,小队人员为了测出坑深,采取如下方案:如图所示,在深坑左侧用观测仪从观测出发点A观测深坑底部P,且观测视线刚好经过深坑边缘点M,在深坑右侧用观测仪从观测出发点C观测深坑底部P,且观测视线恰好经过深坑边缘点N.(点E,B,M,N,D,F在同一水平线上)
已知: , 观测仪高 , 观测仪高 , , 深坑宽度.请根据以上数据计算深坑深度多少米?
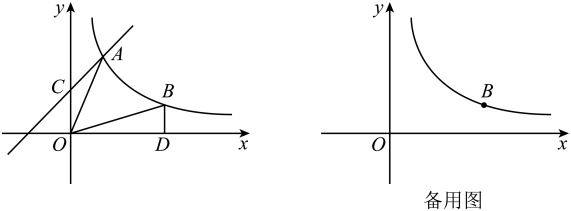
 21. 为传承中华民族优秀传统文化,提高学生文化素养,学校举办“经典诵读”比赛,比赛题目分为“诗词之风”、“散文之韵”和“小说之趣”三组(依次记为A,B,C).彤彤和祺祺两名同学参加比赛,其中一名同学从三组题目中随机抽取一组,然后放回,另一名同学再随机抽取一组.(1)、彤彤抽到A组题目的概率是;(2)、请用列表法或画树状图的方法,求彤彤和祺祺抽到相同题目的概率.22. 如图,一次函数的图象与反比例函数的图象交于点A,与y轴交于点B.已知点A的纵坐标为6.
21. 为传承中华民族优秀传统文化,提高学生文化素养,学校举办“经典诵读”比赛,比赛题目分为“诗词之风”、“散文之韵”和“小说之趣”三组(依次记为A,B,C).彤彤和祺祺两名同学参加比赛,其中一名同学从三组题目中随机抽取一组,然后放回,另一名同学再随机抽取一组.(1)、彤彤抽到A组题目的概率是;(2)、请用列表法或画树状图的方法,求彤彤和祺祺抽到相同题目的概率.22. 如图,一次函数的图象与反比例函数的图象交于点A,与y轴交于点B.已知点A的纵坐标为6. (1)、求k的值:(2)、点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.23. 如图,在正方形中, , 分别是其外角和的平分线,点E在射线上,点F在射线上,连接 , , .已知.
(1)、求k的值:(2)、点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.23. 如图,在正方形中, , 分别是其外角和的平分线,点E在射线上,点F在射线上,连接 , , .已知. (1)、求证:以线段 , , 为三边组成的三角形是直角三角形;(2)、若为等腰直角三角形,探究线段 , 之间的数量关系;(3)、当时,请求出的值.24. 某大型批发商场平均每天可售出某款商品3000件,售出1件该款商品的利润是10元. 经调查发现,若该款商品的批发价每降低1元,则每天可多售出1000件.为了使每天获得的利润更多,该批发商场决定降价x元销售该款商品.(1)、当x为多少元时,该批发商场每天卖出该款商品的利润为40000元?(2)、若按照这种降价促销的策略,该批发商场每天卖出该款商品的利润能达50000元吗?若能,请求出x的值,若不能,请说明理由.
(1)、求证:以线段 , , 为三边组成的三角形是直角三角形;(2)、若为等腰直角三角形,探究线段 , 之间的数量关系;(3)、当时,请求出的值.24. 某大型批发商场平均每天可售出某款商品3000件,售出1件该款商品的利润是10元. 经调查发现,若该款商品的批发价每降低1元,则每天可多售出1000件.为了使每天获得的利润更多,该批发商场决定降价x元销售该款商品.(1)、当x为多少元时,该批发商场每天卖出该款商品的利润为40000元?(2)、若按照这种降价促销的策略,该批发商场每天卖出该款商品的利润能达50000元吗?若能,请求出x的值,若不能,请说明理由.