四川省成都市成华区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-14 类型:期末考试
一、单选题
-
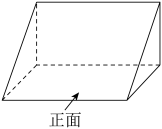
1. 下列各点在反比例函数y=-图象上的是( )A、(1,3) B、(-3,-1) C、(-1,3) D、(3,1)2. 如图是《九章算术》中“堑堵”的立体图形,它的左视图为( )
 A、
A、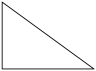 B、
B、 C、
C、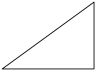 D、
D、 3. 下列一元二次方程有实数解的是( )A、 B、 C、 D、4. 下列命题为假命题的是( )A、对角线相等的平行四边形是矩形 B、对角线互相垂直的平行四边形是菱形 C、有一个内角是直角的平行四边形是正方形 D、有一组邻边相等的矩形是正方形5. 若关于x的一元二次方程x2+6x+c=0配方后得到方程(x+3)2=2c,则c的值为( )A、﹣3 B、0 C、3 D、96. 在同一平面直角坐标系中,函数和的图像大致是( )A、
3. 下列一元二次方程有实数解的是( )A、 B、 C、 D、4. 下列命题为假命题的是( )A、对角线相等的平行四边形是矩形 B、对角线互相垂直的平行四边形是菱形 C、有一个内角是直角的平行四边形是正方形 D、有一组邻边相等的矩形是正方形5. 若关于x的一元二次方程x2+6x+c=0配方后得到方程(x+3)2=2c,则c的值为( )A、﹣3 B、0 C、3 D、96. 在同一平面直角坐标系中,函数和的图像大致是( )A、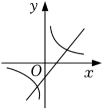 B、
B、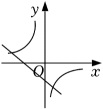 C、
C、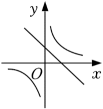 D、
D、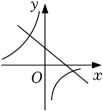 7. 如图,在矩形中,对角线相交于点O,点E是边的中点,点F在对角线上,且 , 连接.若 , 则的长为( )
7. 如图,在矩形中,对角线相交于点O,点E是边的中点,点F在对角线上,且 , 连接.若 , 则的长为( )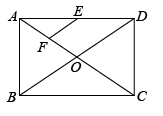 A、 B、3 C、4 D、58. 如图,在中,点 , , 分别在边 , , 上,连接 , , 已知四边形是平行四边形,.若的面积为 , 则平行四边形的面积为( )
A、 B、3 C、4 D、58. 如图,在中,点 , , 分别在边 , , 上,连接 , , 已知四边形是平行四边形,.若的面积为 , 则平行四边形的面积为( )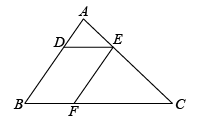 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
9. 已知 ,若b+d≠0,则 = .10. 当重复试验次数足够多时,可用频率来估计概率.历史上数学家皮尔逊(Pearson)曾在实验中掷均匀的硬币24000次,正面朝上的次数是12012次,频率约为0.5,则掷一枚均匀的硬币,正面朝上的概率是 .11. 如图,点是反比例函数的图象上任意一点,过点作轴的垂线,垂足为 , 连接 , 则的面积为.
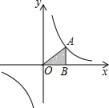 12. 关于的一元二次方程有实数根,则的取值范围为.13. 如图,在中, , , , 以点B为圆心,长为半径画弧,与交于点D,再分别以A,D为圆心,大于的长为半径画弧,两弧交于点M,N,作直线 , 分别交 , 于点E,F,则线段的长为.
12. 关于的一元二次方程有实数根,则的取值范围为.13. 如图,在中, , , , 以点B为圆心,长为半径画弧,与交于点D,再分别以A,D为圆心,大于的长为半径画弧,两弧交于点M,N,作直线 , 分别交 , 于点E,F,则线段的长为.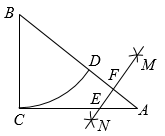 14. 已知反比例函数的图象经过点 , 则a的值为 .15. 已知、是一元二次方程的两个根,则的值为.16. 如图,点E,F,G,H分别是正方形四边的中点, , , , 围成图中阴影部分.随机地往正方形内投掷飞镖,飞镖击中阴影部分的概率是.
14. 已知反比例函数的图象经过点 , 则a的值为 .15. 已知、是一元二次方程的两个根,则的值为.16. 如图,点E,F,G,H分别是正方形四边的中点, , , , 围成图中阴影部分.随机地往正方形内投掷飞镖,飞镖击中阴影部分的概率是.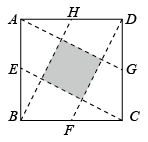 17. 如图是某风车的示意图,其大小相同的四个叶片均匀分布,点M在旋转中心O的正下方.某一时刻,太阳光恰好垂直照射叶片 , 叶片影子为线段 , 测得米,米,此时垂直于地面的标杆与它的影子的比为(其中点M,C,D,F,G在水平地面上),则的高度为米,叶片的长为米.
17. 如图是某风车的示意图,其大小相同的四个叶片均匀分布,点M在旋转中心O的正下方.某一时刻,太阳光恰好垂直照射叶片 , 叶片影子为线段 , 测得米,米,此时垂直于地面的标杆与它的影子的比为(其中点M,C,D,F,G在水平地面上),则的高度为米,叶片的长为米.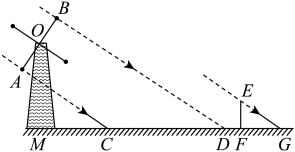 18. 如图,在矩形中, . 若点E是边AD上的一个动点,过点E作且分别交对角线AC,直线BC于点O、F,则在点E移动的过程中,的最小值为 .
18. 如图,在矩形中, . 若点E是边AD上的一个动点,过点E作且分别交对角线AC,直线BC于点O、F,则在点E移动的过程中,的最小值为 .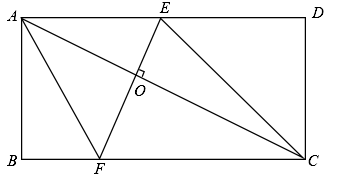
三、解答题
-
19.(1)、解方程:(x+8)(x+1)=-12;(2)、解方程:.20. 为落实国家“双减”政策,学校在课后托管时间里开展了“A-音乐、B-体育、C-文学、D-美术”四项社团活动.学校从全校名学生中随机抽取了部分学生进行“你最喜欢哪一种社团活动”的问卷调查(每人必选且只选一种),并根据调查结果,绘制了如图所示的两幅不完整的统计图.根据图中信息,解答下列问题:
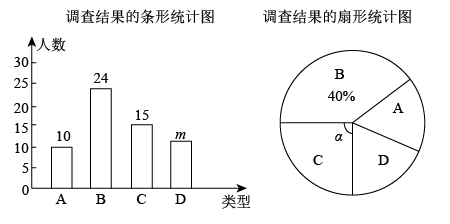 (1)、参加调查的学生共有人;条形统计图中m的值为;扇形统计图中的度数为;根据调查结果,可估计该校名学生中最喜欢“音乐”社团的约有人;(2)、现从“文学”社团里表现优秀的甲、乙、丙、丁四名同学中随机选取两名参加演讲比赛,请用列表或画树状图的方法求出恰好选中甲和乙两名同学的概率.21. 某市从2020年起连续投入资金用于建设美丽城市,改造老旧小区.已知每年投入资金的增长率相同,其中2020年投入资金1000万元,2020年投入资金1440万元.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2022年老旧小区改造的平均费用为每个80万元.2023年为提高老旧小区品质,每个小区改造费用计划增加20%.如果投入资金年增长率保持不变,求该市2023年最多可以改造多少个老旧小区?22. 如图,点E是正方形 的对角线延长线上一点,连接 , 将绕点B顺时针旋转至 , 连接 , 交于点G.
(1)、参加调查的学生共有人;条形统计图中m的值为;扇形统计图中的度数为;根据调查结果,可估计该校名学生中最喜欢“音乐”社团的约有人;(2)、现从“文学”社团里表现优秀的甲、乙、丙、丁四名同学中随机选取两名参加演讲比赛,请用列表或画树状图的方法求出恰好选中甲和乙两名同学的概率.21. 某市从2020年起连续投入资金用于建设美丽城市,改造老旧小区.已知每年投入资金的增长率相同,其中2020年投入资金1000万元,2020年投入资金1440万元.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2022年老旧小区改造的平均费用为每个80万元.2023年为提高老旧小区品质,每个小区改造费用计划增加20%.如果投入资金年增长率保持不变,求该市2023年最多可以改造多少个老旧小区?22. 如图,点E是正方形 的对角线延长线上一点,连接 , 将绕点B顺时针旋转至 , 连接 , 交于点G.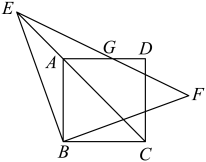 (1)、求证:;(2)、若正方形的边长为4,点G为的中点,求的长.23. 如图,一次函数的图象与反比例函数的图象交于点 , 与y轴交于点B,与x轴交于点.
(1)、求证:;(2)、若正方形的边长为4,点G为的中点,求的长.23. 如图,一次函数的图象与反比例函数的图象交于点 , 与y轴交于点B,与x轴交于点.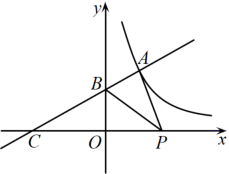 (1)、求k与m的值;(2)、点为x轴正半轴上的一点,且的面积为 , 求a的值.(3)、在(2)的条件下,在平面内是否存在一点Q,使以点A,B,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点Q的坐标;不存在,请说明理由.24. 为防控疫情,学校对学生宿舍进行消毒工作,先经过的集中药物喷洒,再封闭宿舍 , 然后打开门窗进行通风,宿舍内空气中含药量()与时间()之间的函数图象如图所示,打开门窗前为线段和线段 , 打开门窗后为反比例函数关系.
(1)、求k与m的值;(2)、点为x轴正半轴上的一点,且的面积为 , 求a的值.(3)、在(2)的条件下,在平面内是否存在一点Q,使以点A,B,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点Q的坐标;不存在,请说明理由.24. 为防控疫情,学校对学生宿舍进行消毒工作,先经过的集中药物喷洒,再封闭宿舍 , 然后打开门窗进行通风,宿舍内空气中含药量()与时间()之间的函数图象如图所示,打开门窗前为线段和线段 , 打开门窗后为反比例函数关系.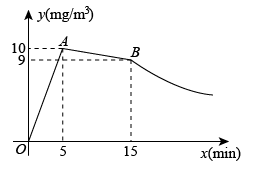 (1)、求线段和反比例函数的表达式;(2)、当室内空气中的含药量不低于且持续时间不低于分钟时,才能有效消毒,请问这次消毒工作是否有效?25. 如图,点A在反比例函数的图像上,点A的纵坐标为3.过点A作x轴的平行线交反比例函数的图像于点C.点P为线段AC上一动点,过点P作的垂线,分别交反比例函数和的图像于点B,D.
(1)、求线段和反比例函数的表达式;(2)、当室内空气中的含药量不低于且持续时间不低于分钟时,才能有效消毒,请问这次消毒工作是否有效?25. 如图,点A在反比例函数的图像上,点A的纵坐标为3.过点A作x轴的平行线交反比例函数的图像于点C.点P为线段AC上一动点,过点P作的垂线,分别交反比例函数和的图像于点B,D.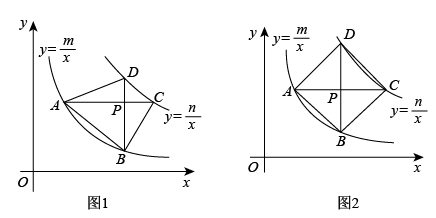 (1)、当时,
(1)、当时,①若点P的横坐标为4(如图1),求直线的函数表达式;
②若点P是的中点(如图2),试判断四边形的形状,并说明理由;
(2)、四边形能否成为正方形?若能,求此时m,n之间的数量关系;若不能,说明理由.26. 如图,在中, , , , 将绕点A逆时针旋转得到.点P,Q分别是 , 上的动点,且 , 连接 , , , .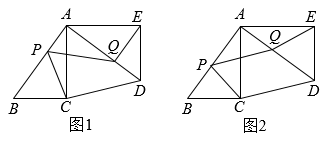 (1)、当时(如图1),求BP的长;(2)、当时(如图2),求BP的长;(3)、是否存在点P,Q,使四边形的面积为?若存在,请求出的长;若不存在,请说明理由.
(1)、当时(如图1),求BP的长;(2)、当时(如图2),求BP的长;(3)、是否存在点P,Q,使四边形的面积为?若存在,请求出的长;若不存在,请说明理由.