四川省巴中市平昌县2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-14 类型:期末考试
一、单选题
-
1. 使二次根式 有意义的x的取值范围是( )A、x>0 B、x>2 C、x≥2 D、x≠22. 下列二次根式中,与不是同类二次根式的是( )A、 B、 C、 D、3. 下列计算中,正确的是( )A、 B、 C、 D、4. 已知 , 则的值为( )A、 B、 C、 D、5. “射击运动员射击一次,命中靶心”这个事件是( )
A、确定事件 B、必然事件 C、不可能事件 D、不确定事件6. 在中, , 则的值为( )A、 B、 C、 D、7. 若关于x的方程x2+3x+a=0有一个根为-1,则另一个根为( )A、-2 B、2 C、4 D、-38. 用配方法解一元二次方程时,下列变形正确的是( )A、 B、 C、 D、9. 某公司今年1月份生产口罩250万只,按计划第一季度的总生产量要达到910万只.设该公司2、3两个月生产量的月平均增长率为 , 根据题意列方程正确的是( )A、 B、 C、 D、10. 如图,在Rt△ABC中,∠CAB=90,AD⊥BC于点D,若BD=2,sinC= ,则线段 AB 的长为( ) A、10 B、4 C、4 D、211. 如图,在△ABC中,D、E分别为AB、AC的中点,点F在DE上,且AF⊥CF,若AC=3,BC=6,则DF的长为( )
A、10 B、4 C、4 D、211. 如图,在△ABC中,D、E分别为AB、AC的中点,点F在DE上,且AF⊥CF,若AC=3,BC=6,则DF的长为( ) A、1.5 B、1 C、0.5 D、212. 如图,某商店营业大厅自动扶梯 的坡度为 ,过点B作 ,垂足为点C.若大厅水平距离 的长为 ,则两层之间的高度 为( )
A、1.5 B、1 C、0.5 D、212. 如图,某商店营业大厅自动扶梯 的坡度为 ,过点B作 ,垂足为点C.若大厅水平距离 的长为 ,则两层之间的高度 为( )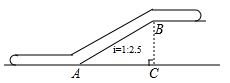 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若计算 的结果为正整数,则无理数m的值可以是 . (写出一个符合条件的即可)14. 计算的结果为.15. 设x1 , x2是方程2x2-x-1=0的两个实数根,则x1+x2=.16. 在正方形网格中,的位置如图所示,则的值为
 17. 构建几何图形解决代数问题是“数形结合”思想的重要体现,在计算tan 15°时,如图,在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB到点D,使BD=AB,连接AD,得∠D=15°, 所以tan 15°==.类比这种方法,计算的值为.
17. 构建几何图形解决代数问题是“数形结合”思想的重要体现,在计算tan 15°时,如图,在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB到点D,使BD=AB,连接AD,得∠D=15°, 所以tan 15°==.类比这种方法,计算的值为. 18. 如图,在矩形ABCD中,E是BC边的中点,DE⊥AC,垂足为点F,连接BF,下列四个结论:①CEF∽ACD;②=2;③sin∠CAD=;④AB=BF.其中正确的结论有(写出所有正确结论的序号).
18. 如图,在矩形ABCD中,E是BC边的中点,DE⊥AC,垂足为点F,连接BF,下列四个结论:①CEF∽ACD;②=2;③sin∠CAD=;④AB=BF.其中正确的结论有(写出所有正确结论的序号).
三、解答题
-
19. 计算解方程(1)、(2)、(3)、(4)、20. 已知为方程的根,化简并求值.21. 已知关于x的一元二次方程 有实数根.(1)、求m的取值范围;(2)、如果方程的两个实数根为 、 ,且 ,求m的取值范围.22. 如图,的三个顶点坐标分别为.
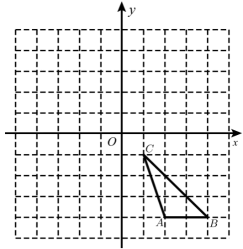 (1)、直接写出关于轴对称的三个顶点的坐标;(2)、画出绕点逆时针旋转后的;(3)、以点为位似中心,在网格中画出的位似图形 , 使与的相似比为.23. 放假期间,小明和小华准备到大众湖度假区(记为A)、东台森林公园(记为B)、欧风花街(记为C)的其中一个景点去游览,他们各自在这三个景点中任选一个,每个景点都被选中的可能性相同.(1)、小明选择去大众湖度假区的概率是;(2)、用树状图或列表的方法求小明和小华分别去不同景点游览的概率.24. 如图,矩形ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点E.
(1)、直接写出关于轴对称的三个顶点的坐标;(2)、画出绕点逆时针旋转后的;(3)、以点为位似中心,在网格中画出的位似图形 , 使与的相似比为.23. 放假期间,小明和小华准备到大众湖度假区(记为A)、东台森林公园(记为B)、欧风花街(记为C)的其中一个景点去游览,他们各自在这三个景点中任选一个,每个景点都被选中的可能性相同.(1)、小明选择去大众湖度假区的概率是;(2)、用树状图或列表的方法求小明和小华分别去不同景点游览的概率.24. 如图,矩形ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点E.①求证:△ABM∽△EMA.
②若AB=4,BM=3,求sinE的值.
 25. 如图,甲、乙两座建筑物的水平距离BC为34 m,从甲建筑物的顶部A处测得乙建筑物的顶部D处的俯角为48°,测得乙建筑物的底部C处的俯角为58°,求乙建筑物的高度CD.(结果精确到0.1m.参考数据:sin 48°≈0.74, cos 48°≈0.67,tan 48°≈1.11,sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)
25. 如图,甲、乙两座建筑物的水平距离BC为34 m,从甲建筑物的顶部A处测得乙建筑物的顶部D处的俯角为48°,测得乙建筑物的底部C处的俯角为58°,求乙建筑物的高度CD.(结果精确到0.1m.参考数据:sin 48°≈0.74, cos 48°≈0.67,tan 48°≈1.11,sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60) 26. 某商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
26. 某商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.①若降价6元时,则平均每天销售数量为多少件?
②当每件商品降价多少元时,该商店每天销售利润为1200元?