福建省福州市2023年九年级上学期期末模拟考试数学试题(福州一检押题卷)
试卷更新日期:2023-02-14 类型:中考模拟
一、单选题
-
1. 下列图案中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 方程的根是( )A、 B、 C、 , D、 ,3. 下列事件中,是必然事件的是( )A、任意买一张电影票,座位号是偶数 B、在平面内,平行四边形的两条对角线相交 C、掷两次硬币,必有一次正面朝上 D、小明参加2023年体育中考测试,“坐位体前屈”项目获得满分4. 若正六边形的边长等于4,则它的面积等于( )A、 B、 C、 D、5. 在反比例函数图象上有三个点 , 、 , 、 , , 若 , 则下列结论正确的是( )A、 B、 C、 D、6. 如图是二次函数的部分图象,则关于的一元二次方程的解是( )
2. 方程的根是( )A、 B、 C、 , D、 ,3. 下列事件中,是必然事件的是( )A、任意买一张电影票,座位号是偶数 B、在平面内,平行四边形的两条对角线相交 C、掷两次硬币,必有一次正面朝上 D、小明参加2023年体育中考测试,“坐位体前屈”项目获得满分4. 若正六边形的边长等于4,则它的面积等于( )A、 B、 C、 D、5. 在反比例函数图象上有三个点 , 、 , 、 , , 若 , 则下列结论正确的是( )A、 B、 C、 D、6. 如图是二次函数的部分图象,则关于的一元二次方程的解是( )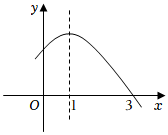 A、 , B、 , C、 , D、 ,7. 如图,在绕点O逆时针旋转80°得到 , 若 , 则的度数是( )
A、 , B、 , C、 , D、 ,7. 如图,在绕点O逆时针旋转80°得到 , 若 , 则的度数是( )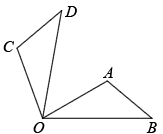 A、30° B、40° C、50° D、60°8. 如图,四边形内接于 , , , 则的半径为( )
A、30° B、40° C、50° D、60°8. 如图,四边形内接于 , , , 则的半径为( )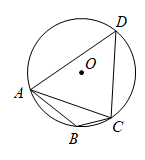 A、4 B、 C、 D、9. 是的直径,弦 , 则( )
A、4 B、 C、 D、9. 是的直径,弦 , 则( )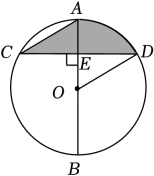 A、π B、2π C、 D、4π10. 如图,已知 , 分别为正方形的边 , 的中点,与交于点.则下列结论:① , ② , ③ , ④.其中正确结论的有( )
A、π B、2π C、 D、4π10. 如图,已知 , 分别为正方形的边 , 的中点,与交于点.则下列结论:① , ② , ③ , ④.其中正确结论的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
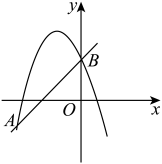
11. 抛物线与直线交于一点,则.12. 如图,已知抛物线与直线交于、两点,则关于的不等式的解集是.
 13. 如图,在中, , 点D在边上,点E在边上且.只需添加一个条件即可证明 , 这个条件可以是(写出一个即可).
13. 如图,在中, , 点D在边上,点E在边上且.只需添加一个条件即可证明 , 这个条件可以是(写出一个即可). 14. 如图,在中, , 将绕点顺时针旋转后,得到 , 且在边上,则的度数为 .
14. 如图,在中, , 将绕点顺时针旋转后,得到 , 且在边上,则的度数为 .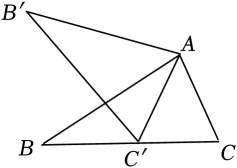 15. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.
15. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.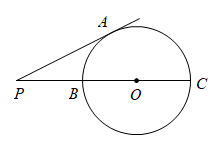 16. 如图,已知正比例函数与反比例函数交于、两点,点是第三象限反比例函数上一点,且点在点的左侧,线段交轴的正半轴于点 , 若的面积是 , 则点的坐标是.
16. 如图,已知正比例函数与反比例函数交于、两点,点是第三象限反比例函数上一点,且点在点的左侧,线段交轴的正半轴于点 , 若的面积是 , 则点的坐标是.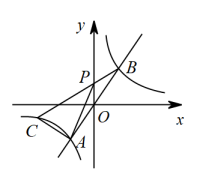
三、解答题
-
17. 用适当的方法解下列一元二次方程:(1)、.(2)、.18. 已知关于x的一元二次方程.(1)、判断这个一元二次方程的根的情况.(2)、若等腰三角形的一边长为3,另两边的长恰好是这个方程的两个根,求这个等腰三角形的周长.19. 已知二次函数的图像经过点 , .(1)、求 , 的值;(2)、若点 , 在二次函数图像上,其中 , 当时,求的取值的范围.20. 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.
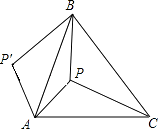 (1)、求点P与点P′之间的距离;(2)、求∠APB的度数.21. 如图,在中, , 以点A为圆心,长为半径作圆,交于点D,交于点E,连接.
(1)、求点P与点P′之间的距离;(2)、求∠APB的度数.21. 如图,在中, , 以点A为圆心,长为半径作圆,交于点D,交于点E,连接.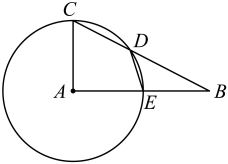 (1)、若 , 求的度数;(2)、在(1)的基础上,若 , 求.22. 如图,一次函数的图像与轴,轴分别交于 , 两点,与反比例函数的图像分别交于 , 两点,已知点坐标是 , .
(1)、若 , 求的度数;(2)、在(1)的基础上,若 , 求.22. 如图,一次函数的图像与轴,轴分别交于 , 两点,与反比例函数的图像分别交于 , 两点,已知点坐标是 , .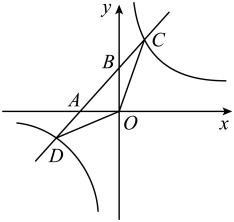 (1)、求一次函数与反比例函数的解析式:(2)、直接写出不等式的解集(3)、求的面积.23. 某超市以元个购进一批新的玩具,当以17元个出售时,每天可以售出50个,国庆期间,在确保不亏本的前提下采取降价促销,经调查发现,当售价每降0.5元个,每天可多卖出5个玩具;(1)、设玩具的售价降低了元,每天的销售量为个,写出与的函数关系式,及自变量的取值范围;(2)、设销售这种玩具每天可获利为元,求与之间的函数表达式;(3)、这种玩具的售价定为多少时,超市每天销售这种玩具获得的利润最大?24. 某校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了5个活动小组(每位学生只能参加一个活动小组): . 音乐; . 体育; . 美术; . 阅读; . 人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
(1)、求一次函数与反比例函数的解析式:(2)、直接写出不等式的解集(3)、求的面积.23. 某超市以元个购进一批新的玩具,当以17元个出售时,每天可以售出50个,国庆期间,在确保不亏本的前提下采取降价促销,经调查发现,当售价每降0.5元个,每天可多卖出5个玩具;(1)、设玩具的售价降低了元,每天的销售量为个,写出与的函数关系式,及自变量的取值范围;(2)、设销售这种玩具每天可获利为元,求与之间的函数表达式;(3)、这种玩具的售价定为多少时,超市每天销售这种玩具获得的利润最大?24. 某校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了5个活动小组(每位学生只能参加一个活动小组): . 音乐; . 体育; . 美术; . 阅读; . 人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.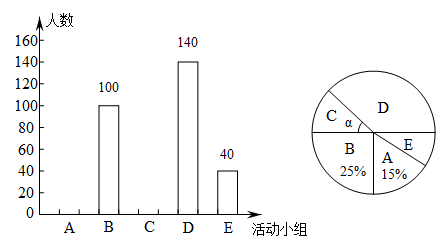
根据图中信息,解答下列问题:
(1)、①此次调查一共随机抽取了 ▲ 名学生;②补全条形统计图(要求在条形图上方注明人数);
③扇形统计图中圆心角 ▲ 度;
(2)、若该校有2800名学生,估计该校参加组(阅读)的学生人数;(3)、学校计划从组(人工智能)的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.25. 已知:在中, , , 是的中点,以为直径的分别交、于点、 , 点位于点下方,连接交于点.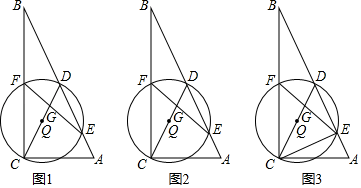 (1)、求证:F是的中点;(2)、如图1,如果 , 求的长;(3)、如图2,设 , , 求y关于x的函数关系式及自变量x的取值范围;
(1)、求证:F是的中点;(2)、如图1,如果 , 求的长;(3)、如图2,设 , , 求y关于x的函数关系式及自变量x的取值范围;