人教版七年级上角的旋转专题训练

试卷更新日期：2023-02-14 类型：复习试卷

进入 出卷网 下载

一、综合题

  • 1. 一副三角尺（分别含45° ， 45° ， 90°和30° ， 60° ， 90°）按如图1所示摆放在量角器上，边PD与量角器0°刻度线重合，边AP与量角器180°刻度线重合(∠APB=45° ， ∠DPC=30°) ， 将三角尺ABP绕量角器中心点P以每秒15°的速度顺时针旋转，当边PB与0°刻度线重合时停止运动，设三角尺ABP的运动时间为t.

    (1)、当t=3时，边PB经过的量角器刻度线对应的度数是度；
    (2)、如图2，若在三角尺ABP开始旋转的同时，三角尺PCD也绕点P以每秒5°的速度逆时针旋转，当三角尺ABP停止旋转时，三角尺PCD也停止旋转，∠MPN=180°.

    ①用含t的代数式表示：∠NPD=      ▲      ；∠MPB=      ▲      ；当t为何值时，∠BPC=5°

    ②从三角尺ABP与三角尺PCD第一对直角边和斜边重叠开始起到另一对直角边和斜边重叠结束止，经过的时间t为      ▲      秒 ．

    查看试题解析

  • 2. 已知∠AOB=130° ， ∠COD=80° ， OM ， ON分别是∠AOB和∠COD的平分线.

    (1)、如图1，如果OA ， OC重合，且OD在∠AOB的内部，则∠MON=度；
    (2)、如图2，固定∠AOB ， 将图1中的∠COD绕点O顺时针旋转n°（0<n≤90）.∠MON与旋转度数n°有怎样的数量关系？说明理由；
    (3)、如果∠AOB的位置和大小不变，∠COD的边OD的位置不变，改变∠COD的大小；将图1中的OC绕着O点顺时针旋转m°（0<m<100），如图3，请直接写出∠MON与旋转度数m°之间的数量关系：.

    查看试题解析

  • 3. 已知OC是∠AOB内部的一条射线，M ， N分别为OA ， OC上的点，线段OM ， ON同时分别以20°/s ， 10°/s的速度绕点O逆时针旋转一周，设旋转时间为t秒.

    (1)、如图①，若∠AOB=120° ， 当OM、ON逆时针旋转到OM'、ON'处，

    ①若OM ， ON旋转时间t=3时，则∠BON'+∠COM'=      ▲      ；

    ②若OM'平分∠AOC ， ON'平分∠BOC ， 求∠M'ON'的值；

    (2)、如图②，若∠AOB=3∠BOC ， OM ， ON分别在∠AOC ， ∠BOC内部旋转时，请猜想∠COM与∠BON的数量关系，并说明理由.
    (3)、若∠AOC=70° ， OM ， ON在旋转的过程中，当∠MON=20° ， 求t的值.

    查看试题解析

  • 4. 将一副直角三角板如图1摆放在直线AD上(直角三角板OBC和直角三角板MON ， ∠OBC=90° ， ∠BOC=45° ， ∠MON=90° ， ∠MNO=30°) ， 保持三角板OBC不动，将三角板MON绕点O以每秒10°的速度顺时针旋转直至ON边第一次重合在直线AD上，整个过程时间记为t秒．

    (1)、从旋转开始至结束，整个过程共持续了秒；
    (2)、如图2，旋转三角板MON ， 使得OM、ON在直线OC的异侧，请直接写出∠CON与∠AOM数量关系；

    如图3，继续旋转三角板MON ， 使得OM、ON同时在直线OC的右侧，请问上面的数量关系是否仍然成立？并说明理由．

    (3)、若在三角板MON旋转的同时，另一个三角板OBC也绕点O以每秒12°的速度顺时针旋转，当ON边第一次重合在直线AD上时两三角板同时停止．

    ①试用字母t分别表示∠AOM与∠AOC；

    ②在旋转的过程中，当t为何值时OM平分∠AOC ．

    查看试题解析

  • 5. 已知，O是直线AB上的一点，∠COD是直角，OE平分∠BOC.

    (1)、如图1，若∠AOC=36° ， 求∠DOE的度数；
    (2)、将图1中的∠DOC绕顶点O顺时针旋转至图2的位置.

    ①探究∠AOD（小于平角）和∠DOE的度数之间的关系，写出你的结论，并说明理由.

    ②在∠AOC（小于平角）的内部有一条射线OF，满足：3∠COF+2∠BOE=12(∠AOD+4∠AOF) ， 试确定∠AOF与∠BOE的之间的数量关系，并说明理由.

    查看试题解析

  • 6. 已知：O是直线AB上的一点，∠COD是直角，OE平分钝角∠BOC ．

    (1)、如图1，若∠AOC=40° ， 求∠DOE的度数；
    (2)、如图2，OF平分∠BOD ， 求∠EOF的度数；
    (3)、当∠AOC=40°时，∠COD绕点O以每秒5°沿逆时针方向旋转t秒(0<t<36) ， 请探究∠AOC和∠DOE之间的数量关系．（直接写出结果）

    查看试题解析

  • 7. 如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC＝60°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

    (1)、将图1中的三角板绕点O处逆时针旋转至图2，使一边OM在∠BOC的内部．且恰好平分∠BOC，求∠CON与∠AOM的度数．
    (2)、将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部．请探究：∠CON与∠AOM之间的数量关系，并说明理由．
    (3)、将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，第t秒时．直线ON恰好平分锐角∠AOC，则t的值为秒（直接写出结果）．

    查看试题解析

  • 8. 如图1，一块三角板的一条直角边OC放在直线AB上．将图1中的三角板绕点O顺时针旋转，使它的两直角边OC、OD均在直线AB的上方，得图2；将图1中的三角板绕点O逆时针旋转，使它的直角边OC在直线AB下方，OD在直线AB的上方得图3．OE始终平分∠AOD ．

    (1)、图1中，∠COE的度数为 ， ∠BOD=；图2中，若∠COE=35° ， 则∠BOD= ．
    (2)、在图2中，猜想∠BOD与∠COE数量关系，并说明理由．
    (3)、在图3中，直接写出∠BOD与∠COE的数量关系．不必说明理由．

    查看试题解析

  • 9. 将两块直角三角板的顶点A叠在一起，已知∠BAC＝30°，∠DAE＝90°，将三角板ADE绕点A旋转，在旋转过程中，保持∠BAC始终在∠DAE的内部．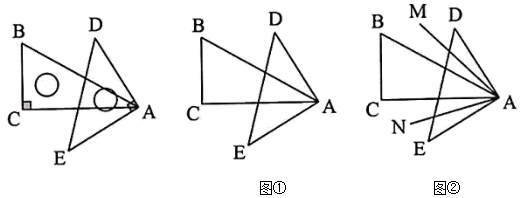

    (1)、如图①，若∠BAD＝25°，求∠CAE的度数．
    (2)、如图①，∠BAE与∠CAD有什么数量关系，请说明理由．
    (3)、如图②，若AM平分∠BAD，AN平分∠CAE，问在旋转过程中，∠MAN的大小是否发生改变？若不变，请说明理由；若改变，请求出变化范围．

    查看试题解析

  • 10. 如图1，∠AOB是平角，∠COD是直角，射线OB在∠COD内部，OE，OF分别是∠BOD，∠AOC的平分线．

    (1)、如图1，若OB是∠COD的平分线，求∠AOF的度数；
    (2)、如图1，求∠EOF的度数；
    (3)、若改变∠COD的位置变化，如图2，当∠COD在直线AB的上方时，如图3，当射线OA在∠COD内部时，如图4，当∠COD在直线AB的下方时，∠EOF的度数发生变化吗？若不变，请直接写出∠EOF的度数；若不确定，请说明理由．

    查看试题解析

  • 11. 定义：从一个角的顶点出发，在角的内部引两条射线，如果这两条射线所成的角等于这个角的一半，那么这两条射线所成的角叫做这个角的内半角，如图1，若∠COD=12∠AOB ， 则∠COD是∠AOB的内半角．

    (1)、如图1，∠AOB=80° ， ∠AOC=25° ， ∠COD是∠AOB的内半角，则∠BOD=；
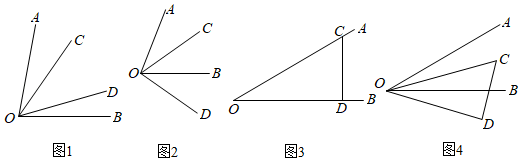    (2)、如图2，已知∠AOB=60° ， 将∠AOB绕点O按顺时针方向旋转一个角度α(0<α<60°)得∠COD ， 当旋转的角度α为何值时，∠COB是∠AOD的内半角；
    (3)、已知∠AOB=30° ， 把一块含有30°角的三角板如图3叠放，将三角板绕顶点O以3度/秒的速度按顺时针方向旋转（如图4) ， 问：在旋转一周的过程中，射线OA、OB、OC、OD能否构成内半角？若能，请直接写出旋转的时间；若不能，请说明理由．

    查看试题解析

  • 12. 有两个形状、大小完全相同的直角三角板ABC和CDE ， 其中∠ACB=∠DCE=90° ． 将两个直角三角板ABC和CDE如图①放置，点A、C、E在直线MN上．

    (1)、三角板CDE位置不动，将三角板ABC绕点C顺时针旋转一周，

    ①在旋转过程中，若∠BCD=30° ， 求∠ACE得度数；

    ②在旋转过程中，∠BCD与∠ACE有怎样的数量关系？请依据图②说明理由．

    (2)、在图①基础上，三角板ABC和CDE同时绕点C顺时针旋转，若三角板ABC的边AC从CM处开始绕点C顺时针旋转，转速为10°/秒，同时三角板CDE的边CE从CN处开始绕点C顺时针旋转，转速为1°/秒，当AC旋转一周再落到CM上时，两三角板都停止转动．如果设旋转时间为t秒，请结合图①完成在旋转过程中，当t=秒时，两三角板重合．在两三角板重合之前当t=秒时，有∠ACE=3∠BCD ．

    查看试题解析

  • 13. 已知：如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC：∠BOC＝1：5．将一等腰直角三角板的直角顶点放在点O处，一直角边ON在射线OB上，另一直角边OM在直线AB的下方．

    (1)、将图1中的等腰直角三角板绕点O以每秒3°的速度逆时针方向旋转一周，直角边ON旋转后的对应边为ON'，直角边OM旋转后的对应边为OM'．在此过程中，经过t秒后，OM'恰好平分∠BOC，求t的值；
    (2)、如图2，在（1）问的条件下，若等腰直角三角板在转动的同时，射线OC也绕点O以每秒4°的速度顺时针方向旋转，射线OC旋转后的对应射线为OC'．当射线OC'落在射线OC的反向延长线上时，射线OC和等腰直角三角板同时停止运动．在此过程中，是否存在某一时刻t，使得OC'//M'N'．若存在，请求出t的值，若不存在，诮说明理由；
    (3)、如图3，在（1）问的条件下，若等腰直角三角板在转动的同时，射线OC也绕点O以每秒5°的速度顺针方向旋转，射线OC旋转后的对应射线为OC'．当等腰直角三角板停止运动时，射线OC也停止运动．在整个运动过程中．经过l秒后，∠M'ON'的某一边恰好平分∠AOC'，请直接写出所有满足条件的t的值．

    查看试题解析

  • 14. 如图，以直线AB上一点O为端点作射线OC，将一块直角三角板的直角顶点放在O处．（注：∠DOE＝90°）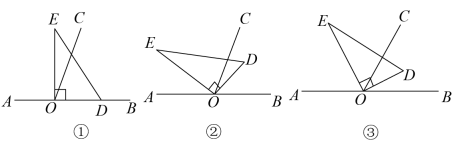

    (1)、如图①，若直角三角板DOE的一边OD放在射线OB上，且∠BOC＝70°，则∠COE＝°；
    (2)、如图②，将直角三角板DOE绕点O逆时针方向转动到某个位置时，∠BOC＝70°，使OD在∠BOC内部，且满足∠AOE＝5∠COD，求∠BOD的度数；
    (3)、如图③，将直角三角板DOE绕点O逆时针方向转动到如图所示位置时，若OE恰好平分∠AOC，试说明OD所在射线是∠BOC的平分线．

    查看试题解析

  • 15. 已知∠AOB=160°，∠COE是直角，OF平分∠AOE.

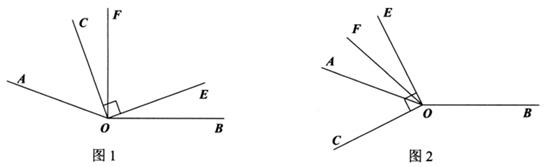    (1)、如图1，若∠COF=32°，则∠BOE=；
    (2)、如图1，若∠COF=m°，则∠BOE=；∠BOE与∠COF的数量关系为.
    (3)、在已知条件不变的前提下，当∠COE绕点О逆时针转动到如图2的位置时，第（2）问中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.

    查看试题解析