人教版七年级上线段动点专题训练

试卷更新日期：2023-02-14 类型：复习试卷

进入出卷网下载

一、综合题

1. 已知在数轴上点M、N表示的数分别为a，b，点M、N两点之间的距离表示为 $| a - b |$ 或 $| b - a |$ ，记为 $| M N | = | a - b | = | b - a |$ ．如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．点P是数轴上任意一点，

(1)、数轴上点B表示的数是；

(2)、如果点P到点A、点B的距离相等，那么点P表示的数是；

(3)、若点P到点A、点B的距离之和等于14，则点P表示的数为；

(4)、若点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动．动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，运动时间为t．求：
①当 $t = 1$ 秒时P，Q两点间的距离为 ▲ ；

②当点P运动多少秒时，点P与点Q相遇？

③当点P与点Q间的距离为8个单位长度时t的值为 ▲ ．

查看试题解析
2. 如图1，已知数轴上有三个点A，B，C，它们对应的数分别为 $a ， b ， c$ ，且 $c-b = b- a$ ，点C对应的数是10.

(1)、若BC=15，求 $a ， b 的值$
图1

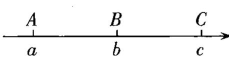(2)、如图2，在（1）的条件下，O为原点，动点P，Q分别从点A，C同时出发，点P向左运动，运动速度为每秒2个单位长度，点Q向右运动，运动速度为每秒1个单位长度，N为OP的中点，M为BQ的中点.
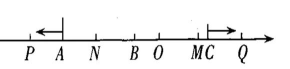图2

用含t的代数式表示PQ，MN.

在点P，Q的运动过程中，PQ与MN存在一个确定的等量关系，请指出它们之间的关系，并说明理由.

查看试题解析
3. 如图，P是线段AB上不同于点A，B的一点，AB＝18cm，C，D两动点分别从点P，B同时出发，在线段AB上向左运动（无论谁先到达A点，均停止运动），点C的运动速度为1cm/s，点D的运动速度为2cm/s．

(1)、若AP＝PB，
①当动点C，D运动了2s时，AC＋PD＝cm；

②当C，D两点间的距离为5cm时，则运动的时间为s；

(2)、当点C，D在运动时，总有PD＝2AC，·
①求AP的长度；
②若在直线AB上存在一点Q，使AQ﹣BQ＝PQ，求PQ的长度．

查看试题解析
4. [背景知识]

(1)、数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离AB＝|a－b|，线段AB的中点表示的数为；

(2)、[问题情境]
如图，数轴上点A表示的数为－2，点B表示的数为8，点P从点A出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动，设运动时间为t秒（t＞0）．
线段AB的中点表示的数为；

(3)、[综合运用]
求当t为何值时PQ＝ $\frac{1}{2}$ AB；

(4)、若点M为PA的中点，点N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化?若变化，请说明理由；若不变，请求出线段MN的长．

查看试题解析
5. 【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离AB= $| a - b |$ ，线段AB的中点表示的数为 $\frac{a + b}{2}$ ．如图，数轴上点A表示的数为 $- 2$ ，点B表示的数为8．

(1)、【综合运用】
填空：A，B两点间的距离AB= ，线段AB的中点表示的数为；

(2)、若M为该数轴上的一点，且满足MA+MB=12，求点M所表示的数；

(3)、若点P从点A出发，以每秒1个单位长度的速度沿数轴向终点B匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动，Q到达A点后，再立即以同样的速度返回B点，当点P到达终点后，P、Q两点都停止运动，设运动时间为t秒（ $t > 0$ ）．当t为何值时，P，Q两点间距离为4．

查看试题解析
6. 如图1，A，B两点在数轴上对应的数分别为-12和 4．

(1)、A，B两点之间的距离为；

(2)、若在数轴上存在一点P，使得 $B P = 3 A P$ ，求点P表示的数．

(3)、如图2，现有动点P，Q，若点P从点A出发，以每秒5个单位长度的速度沿数轴向右运动，同时点Q从点B出发，以每秒1个单位长度的速度沿数轴向左运动，当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动，设运动时间为t秒．求：当 $O P = 2 O Q$ 时t的值．

查看试题解析
7. 如图，在数轴上，O为原点，点A表示的数为－10，点B表示的数为4．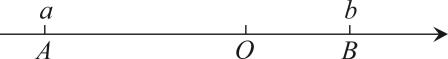

(1)、A，B两点间的距离是．

(2)、若将数轴折叠，使得点A与点B重合，此时原点O与表示数的点重合．

(3)、若点A，B分别以每秒1个单位长度和每秒3个单位长度的速度同时向左运动，则几秒时点B追上点A？

(4)、若点A，B以（3）中的速度相向而行，则几秒时A，B两点相距2个单位长度？

查看试题解析
8. 如图，线段 $A B = 28$ 厘米，点D和点C在线段AB上，且 $A C ： B C = 5 ： 2$ ， $D C ： A B = 1 ： 4$ .点P从点A出发以4厘米/秒的速度沿射线AD向点C运动，点P到达点C所在位置后立即按照原路原速返回，到达点D所在位置后停止运动，点Q从点B出发以1厘米/秒的速度沿着射线BC的方向运动，点Q到达点D所在的位置后停止运动.点P和点Q同时出发，点Q运动的时间为t秒.

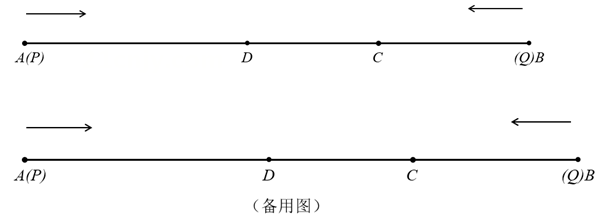(1)、求线段AD的长度；

(2)、当点C恰好为PQ的中点时，求t的值；

(3)、当 $P Q = 7$ 厘米时，求t的值.

查看试题解析
9. 如图，已知A，B两点在数轴上，点A表示的数为−15，OB=2OA，点M以每秒3个单位长度的速度从点A向右运动．点N以每秒2个单位长度的速度从点O向右运动（点M、点N同时出发）

(1)、数轴上点B对应的数是；

(2)、经过几秒，点M、点N到原点O的距离相等？

(3)、当点M运动到什么位置时，恰好使AM=3BN？

查看试题解析
10. 如图，已知数轴上点A，O，B对应的数分别为 $- 2$ ， 0，6，点P是数轴上的一个动点．

(1)、设点P对应的数为x．
①若点P到点A和点B的距离相等，则x的值是；

②若点P在点A的左侧，则 $P A =$ ， $P B =$ （用含x的式子表示）；

(2)、若点P以每秒1个单位长度的速度从点O向右运动，同时点A以每秒3个单位长度的速度向左运动，点B以每秒6个单位长度的速度向右运动，在运动过程中，点M和点N分别是 $A P$ 和 $O B$ 的中点，设运动时间为t．
①移动后，点P在数轴上所表示的数为 ▲ ，点A在数轴上所表示的数为 ▲ ，点B在数轴上所表示的数为 ▲ ，（用含t的式子表示）；

②求 $M N$ 的长（用含的式子表示）；

③当 $t =$ ▲ 时， $M N = A B$ ．

查看试题解析
11. 如图，在数轴上有A、B、C三点，A、B两点所对应的数分别是a，b，且满足a+5是最大的负整数，b﹣3是绝对值最小的有理数，点C在点A的右侧，到点A的距离是2个单位长度．请你解答下列问题：

(1)、点A表示的数是，点B表示的数是，点C表示的数是；

(2)、点P、Q为数轴上两个动点，点P从A点出发速度为每秒1个单位长度，点Q从B点出发速度为每秒2个单位长度，若P、Q两点同时出发，相向而行，运动时间为t秒．求当t为何值时，点P与点Q之间的距离是3个单位长度？

(3)、在（2）的条件下，当点P与点Q之间的距离是3个单位长度时，请你直接写出点C与点Q的距离．

查看试题解析
12. 如图，数轴上点A表示－10，点O表示0，点B表示10，点C表示18.动点P从点A出发，以2单位/秒的速度沿着数轴的正方向运动；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动．当点Р到达点C时，两点都停止运动．设点P运动的时间为t（秒）．

(1)、点A和点C在数轴上相距个单位．

(2)、当 $t = 3$ 时，求点P与点Q的距离．

(3)、求P、Q两点相遇时t的值．

(4)、当线段PO与线段QB的长度相等时，直接写出t的值．

查看试题解析
13. 如图，点A在数轴上所对应的数为2，

(1)、点B在点A左侧且距点A为3个单位长度，则点B所对应的数为，请在数轴上标出点B的位置；

(2)、在（1）的条件下，点A以每秒1个单位长度沿数轴向右运动，点B以每秒2个单位长度沿数轴向左运动，当点A运动到5所在的点处时停止运动，同时点B也停止运动，求此时A，B两点间距离；

(3)、在（2）的条件下，若点A不动，点B沿数轴向右运动，经过t秒A，B两点相距3个单位长度，求t值；

(4)、在（1）的条件下，点A以每秒1个单位长度，点B以每秒2个单位长度同时沿数轴向左运动，当点B运动到所对应的数为m时停止运动，请直接写出此时点A所对应的数为；若点A继续运动，请直接写出当AB＝2时，点A继续运动的距离为．（用含m的式子表示）

查看试题解析
14. 如图，已知数轴上有 $A ， B ， C$ 三点，分别表示有理数 $- 26 ， - 10 ， 10$ ，动点 $P$ 从点 $A$ 出发，以每秒1个单位的速度向终点 $C$ 移动，当点 $P$ 运动到 $B$ 点时，点 $Q$ 从 $A$ 点出发，以每秒3个单位的速度向 $C$ 点运动.

(1)、 $Q$ 点出发3秒后所到的点表示的数为，此时 $P 、 Q$ 两点的距离为.

(2)、问当点 $Q$ 从点 $A$ 点出发几秒钟时，能追上点 $P$ ？

(3)、问当点 $Q$ 从点 $A$ 点出发几秒钟时，点 $P$ 和点 $Q$ 相距2个单位长度？直接写出此时点 $Q$ 在数轴上表示的有理数.

查看试题解析
15. 如图，在数轴上点A，B，C表述的数分别为 $- 2$ 、1、6，点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC．

(1)、请直接写出AB、BC、AC的长度；

(2)、若点D从A点出发，以每秒1个单位长度的速度向左运动，点E从B点出发以每秒2个单位长度的速度向右运动，点F从C点出发以每秒5个单位速度向右运动．设点D、E、F同时出发，运动时间为t秒．
①t秒后，D表示的数为 ▲ ， E表示的数为 ▲ ， F表示的数为 ▲ ．

②试探索： $E F - D E$ 的值是否随着时间t的变化而变化？请说明理由．

(3)、若点M以每秒4个单位的速度从A点出发，点N以每秒3个单位的速度运动从C点出发，设点M、N同时出发，运动时间为t秒．试探究：经过多少秒后，点M、N两点间的距离为14个单位．

查看试题解析