广西壮族自治区玉林市2022-2023学年高二上学期数学1月期末教学质量监测试卷
试卷更新日期:2023-02-13 类型:期末考试
一、单选题
-
1. 在空间直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、2. 直线的倾斜角是( )A、 B、 C、 D、3. 已知圆的方程为 , 则圆心的坐标为( )A、 B、 C、 D、4. 在等比数列中, , , 则等于( )A、 B、5 C、 D、95. 已知抛物线上一点到其焦点的距离为5,则实数的值是( )A、 B、2 C、4 D、86. 如图,空间四边形中, , , .点在上,且 , 为的中点,则( )
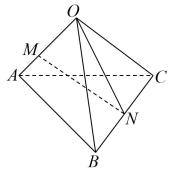 A、 B、 C、 D、7. 在数列中, , 则的值为( )A、 B、7 C、 D、88. 已知双曲线的左、右焦点分别为与是双曲线的左顶点,以为直径的圆与双曲线的一条渐近线交于两点,且 , 则双曲线的离心率为( )A、 B、 C、2 D、
A、 B、 C、 D、7. 在数列中, , 则的值为( )A、 B、7 C、 D、88. 已知双曲线的左、右焦点分别为与是双曲线的左顶点,以为直径的圆与双曲线的一条渐近线交于两点,且 , 则双曲线的离心率为( )A、 B、 C、2 D、二、多选题
-
9. 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.则以下几个命题正确的有( )A、直线l恒过定点(3,1) B、直线l与圆C相切 C、直线l与圆C恒相交 D、直线l与圆C相离10. 关于空间向量,以下说法正确的是( )A、已知任意非零向量 , 若 , 则 B、若对空间中任意一点 , 有 , 则四点共面 C、设是空间中的一组基底,则也是空间的一组基底 D、若空间四个点 , 则三点共线11. 已知数列满足: , , , 3,4,…,则下列说法正确的是()A、 B、对任意 , 恒成立 C、不存在正整数 , , 使 , , 成等差数列 D、数列为等差数列12. 抛物线的焦点为F,P为其上一动点,当P运动到时, , 直线与抛物线相交于A,B两点,点 , 下列结论正确的是( )A、抛物线的方程为 B、存在直线 , 使得A、B两点关于对称 C、的最小值为6 D、当直线过焦点F时,以AF为直径的圆与y轴相切
三、填空题
-
13. 已知直线与垂直,则.14. 在各项均为正数的等比数列中,若 , , 则.15. 如图所示,二面角为 , 是棱上的两点,分别在半平面内 , 且 , , , , , 则的长 .
 16. 已知线段是圆的一条动弦,且 , 若点为直线上的任意一点,则的最小值为.
16. 已知线段是圆的一条动弦,且 , 若点为直线上的任意一点,则的最小值为.四、解答题
-
17. 在中, , , .(1)、求的中线所在直线的方程;(2)、求的面积.18. 如图,在棱长为2的正方体中,分别为 , 的中点,点在上,且 .
 (1)、求证:;(2)、求EF与CG所成角的余弦值.19. 已知数列的前n项和Sn=n2+2n.(1)、求{an}通项公式;(2)、设bn= , 的前n项和为Tn,求Tn20. 已知曲线C是到两个定点 , 的距离之比等于常数的点组成的集合.(1)、求曲线C的方程;(2)、设过点B的直线l与C交于M,N两点;问在x轴上是否存在定点 , 使得为定值?若存在,求出点Q的坐标及定值;若不存在,请说明理由.
(1)、求证:;(2)、求EF与CG所成角的余弦值.19. 已知数列的前n项和Sn=n2+2n.(1)、求{an}通项公式;(2)、设bn= , 的前n项和为Tn,求Tn20. 已知曲线C是到两个定点 , 的距离之比等于常数的点组成的集合.(1)、求曲线C的方程;(2)、设过点B的直线l与C交于M,N两点;问在x轴上是否存在定点 , 使得为定值?若存在,求出点Q的坐标及定值;若不存在,请说明理由.
