广西贵港市2022-2023学年高一上学期数学1月期末质量检测试卷

试卷更新日期：2023-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 命题“ $\forall x \in R$ ， $1 . 6^{x} > x$ ”的否定是（　　）

A、 $\exists x \in R$ ， $1 . 6^{x} \leq x$ B、 $\exists x \notin R$ ， $1 . 6^{x} \leq x$ C、 $\exists x \in R$ ， $1 . 6^{x} < x$ D、 $\forall x \in R$ ， $1 . 6^{x} \leq x$

查看试题解析
2. 若全集 $U = {- 1 ， 2 ， 4 ， 5 ， 19}$ ，集合 $∁_{U} (A ∩ B) = {2 ， 5 ， 19}$ ，则 $A$ 可能为（　　）

A、 ${4}$ B、 ${- 1 ， 19}$ C、 ${- 1 ， 2 ， 4}$ D、 ${4 ， 5 ， 19}$

查看试题解析
3. $t a n (- 420 °) =$ （　　）

A、 $- \sqrt{3}$ B、 $\sqrt{3}$ C、 $- \frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
4. 若函数 $f (x)$ 的定义域为 $(- 2 ， 16)$ ，则函数 $y = \frac{f (2 x)}{l o g_{3} (x - 1)}$ 的定义域为（　　）

A、 $(1 ， 8)$ B、 $(1 ， 32)$ C、 $(1 ， 2) ∪ (2 ， 8)$ D、 $(1 ， 2) ∪ (2 ， 32)$

查看试题解析
5. “ $α$ 是第二象限角”是“ $2 k π < \frac{α}{2} - \frac{π}{4} < \frac{π}{4} + 2 k π ， k \in Z$ ”的（　　）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 已知 $s i n (α - \frac{π}{5}) = \frac{3}{4}$ ，则 $s i n (2 α + \frac{π}{10}) =$ （　　）

A、 $- \frac{7}{16}$ B、 $\frac{7}{16}$ C、 $- \frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
7. 若幂函数 $f (x) = x^{- m^{2} + 2 m + \frac{25}{9}}$ 的图象关于y轴对称， $f (x)$ 解析式的幂的指数为整数， $f (x)$ 在 $(- ∞ ， 0)$ 上单调递减，则 $m =$ （）

A、 $\frac{1}{9}$ B、 $\frac{1}{9}$ 或 $\frac{49}{9}$ C、 $- \frac{1}{3}$ D、 $- \frac{1}{3}$ 或 $\frac{7}{3}$

查看试题解析
8. 若函数 $f (x) = \frac{5}{5^{x} - 5}$ ，则下列函数为奇函数的是（　　）

A、 $g (x) = f (x - 1) - \frac{1}{2}$ B、 $g (x) = f (x + 1) - \frac{1}{2}$ C、 $g (x) = f (x - 1) + \frac{1}{2}$ D、 $g (x) = f (x + 1) + \frac{1}{2}$

查看试题解析

二、多选题

9. 已知函数 $f (x)$ 的图象是一条连续不断的曲线，且有如下对应值表：
x
1
2
3
4
5
$f (x)$
31
$- 15$
$- 7$
23
$- 17$
则一定包含 $f (x)$ 的零点的区间是（）

A、 $(1 ， 2)$ B、 $(2 ， 3)$ C、 $(3 ， 4)$ D、 $(4 ， 5)$

查看试题解析
10. 将 $y = s i n (x + \frac{π}{6})$ 的图象上的所有点的横坐标伸长到原来的2倍，再向左平移 $φ$ （ $φ > 0$ ）个单位长度得到 $f (x)$ 的图象．则（　　）

A、若 $f (x)$ 为奇函数，则 $φ$ 的值可能为 $\frac{π}{3}$ B、若 $f (x)$ 为奇函数，则 $φ$ 的值可能为 $\frac{5 π}{3}$ C、若 $f (x)$ 为偶函数，则 $φ$ 的值可能为 $\frac{2 π}{3}$ D、若 $f (x)$ 为偶函数，则 $φ$ 的值可能为 $\frac{8 π}{3}$

查看试题解析
11. 若 $f (x) = {\begin{array}{l} 2 a^{x} ， x < 2 \\ x^{2} - a x + 4 a ， x \geq 2 \end{array}$ （ $a > 0$ ，且 $a \neq 1$ ）在 $R$ 上单调递增，则 $a$ 的值可能是（　　）

A、 $\frac{1}{2}$ B、 $\sqrt{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
12. 函数 $f (x)$ 满足 $f (x) + f (- x) = 2 x^{2}$ ， $f (1 + x) - f (1 - x) = 8 x$ ， $x \in R$ ，则（　　）

A、 $f (2) = 4$ B、 $f (3) + f (1) = 18$ C、 $y = f (x) - x^{2}$ 为奇函数 D、 $f (x + 2) + f (x) \geq 0$

查看试题解析

三、填空题

13. $s i n 73 ° c o s 13 ° - c o s 73 ° s i n 13 °$ 的值为．

查看试题解析
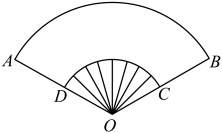
14. “数摺聚清风，一捻生秋意”是宋代朱翌描写折扇的诗句，折扇出入怀袖，扇骨雕琢，是文人雅士的宠物，如图，这是折扇的示意图，已知D为OA中点，OA＝4， $∠ A O B = \frac{3 π}{4}$ （扇环ABCD）部分的面积是．

查看试题解析
15. 若正数 $m ， n$ 满足 $m + n = 8$ ，则 $l o g_{2} m + l o g_{2} n$ 的最大值为．

查看试题解析
16. 已知 $a > 0$ ，函数 $f (x) = {\begin{array}{l} - a x + a - 2 ， x < 0 \\ s i n (a x + \frac{π}{5}) ， 0 \leq x \leq 2 π \end{array}$ ，已知 $f (x)$ 有且仅有5个零点，则 $a$ 的取值范围为．

查看试题解析

四、解答题

17. 求值：

(1)、 $(0.125)^{- \frac{1}{3}} - \sqrt[3]{π} \times π^{\frac{2}{3}} + \sqrt{(3 - π)^{2}}$ ；

(2)、 $2^{l o g_{2} 5} - l g 0.01 + l o g_{a} b \cdot l o g_{b} a$ ．

查看试题解析
18. 已知 $\frac{s i n (α + 2022 π) - 6 s i n (α - \frac{3 π}{2})}{2 c o s (α - π) - s i n α} = - t a n \frac{3 π}{4}$ ．

(1)、求 $t a n α$ 的值；

(2)、求 $s i n α - c o s α$ 的值．

查看试题解析
19. 已知集合 $A = {x | 3 m - 4 < x < 4 - m}$ ， $B = {x | x^{2} - 4 x \geq 0}$ ．

(1)、当 $m = 1$ 时，求 $A \cup B$ ， $(∁_{R} A) ∩ B$ ；

(2)、若 $A ∩ B = A$ ，求 $m$ 的取值范围．

查看试题解析
20. 大西洋鲑鱼每年都要逆流而上，游回产地产卵.研究鲑鱼的科学家发现鲑鱼的油速 $v$ （单位：m/s）可以表示为 $v = \frac{1}{2} l o g_{3} \frac{O}{100}$ ，其中 $O$ 表示鱼的耗氧量的单位数.

(1)、若一条鲑鱼的游速为2m/s，求该鱼的耗氧量的单位数；

(2)、假设甲鲑鱼和乙鲑鱼都做匀速直线运动，乙在甲正前方18m处，12s后甲正好追上乙，求甲鲑鱼与乙鲑鱼耗氧量的单位数的比值.

查看试题解析
21. 已知函数 $f (x) = x^{2} - (a^{2} + 6 a + 9) x + a + 1$ ．

(1)、若 $a > 0$ ，且关于x的不等式 $f (x) < 0$ 的解集是 ${x | m < x < n}$ ，求 $\frac{1}{m} + \frac{1}{n}$ 的最小值；

(2)、设关于x的不等式 $f (x) < 0$ 在 $[0 ， 1]$ 上恒成立，求 $a$ 的取值范围

查看试题解析
22. 已知函数 $f (x) = 2 \sqrt{3} c o s (4 x - \frac{π}{3}) - 2 s i n 2 x c o s 2 x - 2 \sqrt{3} s i n^{2} 2 x + \sqrt{3}$ ．

(1)、求 $f (x)$ 的单调递减区间；

(2)、若 $g (x) = [f (x)]^{2} - (2 m + 2 \sqrt{3}) f (x) + 4 \sqrt{3} m$ 在 $[- \frac{π}{24} ， \frac{π}{12}]$ 上有4个零点，求 $m$ 的取值范围．

查看试题解析

x	1	2	3	4	5
$f (x)$	31	$- 15$	$- 7$	23	$- 17$