广东省河源市2022-2023学年高三上学期数学期末试卷

试卷更新日期：2023-02-13 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x ∣ | x | < 2} ， B = {x ∣ y = l n (a - 2 x)}$ ，且 $A \cap B = {x ∣ - 2 < x < 1}$ ，则 $a =$ （）

A、-4 B、-2 C、2 D、4

查看试题解析
2. 如图，在复平面内，复数 $z_{1} ， z_{2}$ 对应的向量分别是 $\vec{O A} ， \vec{O B}$ ，且复数 $z_{3} = 3 + \frac{z_{1}}{z_{2}}$ ，若复数 $z_{3} ， z_{4}$ 在复平面内的对应点关于虚轴对称，则 $z_{4} =$ （）

A、 $3 - i$ B、 $3 + i$ C、 $- 3 - i$ D、 $- 3 + i$

查看试题解析
3. 已知平面向量 $\vec{a} ， \vec{b}$ 满足 $\vec{a} = (1 ， - 1) ， | \vec{b} | = 1 ， | \vec{a} + 2 \vec{b} | = \sqrt{2}$ ，则向量 $\vec{a}$ 与向量 $\vec{a} + 2 \vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{π}{2}$

查看试题解析
4. 如图所示，一款网红冰激凌可近似地看作是圆锥和半球的组合体，将圆锥外的包装纸展开发现，它是一张半径为6的半圆形纸片，则这个冰激凌的体积为（）

A、 $27 π$ B、 $18 π + 9 \sqrt{3} π$ C、 $36 π + 9 \sqrt{3} π$ D、 $54 π$

查看试题解析
5. 已知角 $α$ 的顶点为坐标原点，始边与 $x$ 轴的非负半轴重合，终边过点 $P (s i n 13 8^{∘} ， c o s 13 8^{∘})$ ，则 $t a n (α + 1 8^{∘}) =$ （）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $- \sqrt{3}$ D、 $- \frac{\sqrt{3}}{3}$

查看试题解析
6. 在数列 ${a_{n}}$ 中， $a_{1} = 1 ， a_{n} > 0$ ，且 $n a_{n + 1}^{2} - a_{n} a_{n + 1} - (n + 1) a_{n}^{2} = 0$ ，则 $a_{20}$ 的值为（）

A、18 B、19 C、20 D、21

查看试题解析
7. $(x - 2 y - 1)^{5}$ 的展开式中含 $x^{2} y^{2}$ 的项的系数为（）

A、 $- 120$ B、60 C、 $- 60$ D、30

查看试题解析
8. 已知函数 $f (x) = x s i n x + c o s x + \frac{1}{2} x^{2}$ ，若 $a = f (l o g_{\frac{1}{2}} e) ， b = f (s i n \frac{1}{2}) ， c = f (l n 3)$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $c > a > b$ B、 $a > c > b$ C、 $a > b > c$ D、 $b > a > c$

查看试题解析

二、多选题

9. 潮汐现象是由于海水受日月的引力在一定的时候发生涨落的现象，一般早潮叫潮，晚潮叫汐，在通常情况下，船在涨潮时驶进航道，靠近船坞卸货后落潮时返回海洋，现有一条货船的吃水深度（船底与水面的距离）为 $4 m$ ，根据安全条例规定至少要有 $2 m$ 的安全间隙（船底与海底的距离），已知某港口在某季节的某一天的时刻 $x$ （单位：小时）与水深 $f (x)$ （单位： $m$ ）的关系为： $f (x) = 2 s i n \frac{π}{6} x + 5 (0 \leq x \leq 24)$ ，则下列说法中正确的有（）

A、相邻两次潮水高度最高的时间间距为 $24 h$ B、18时潮水起落的速度为 $- \frac{π}{3} m / h$ C、该货船在2：00至4：00期间可以进港 D、该货船在13：00至17：00期间可以进港

查看试题解析
10. 如图，已知正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面边长为1，侧棱长为2，点 $E$ 为侧棱 $C C_{1}$ （含端点）上的动点，若平面 $α$ 与直线 $A E$ 垂直，则下列说法正确的有（）

A、直线 $B B_{1}$ 与平面 $α$ 不可能平行 B、直线 $C D$ 与平面 $α$ 不可能垂直 C、 $△ A_{1} B E$ 不可能为直角三角形 D、三棱锥 $B_{1} - A_{1} B E$ 的体积是正四棱柱体积的 $\frac{1}{6}$

查看试题解析
11. 已知 $f (x)$ 是定义在 $R$ 上的奇函数， $f (x)$ 的图象关于 $x = 1$ 对称，当 $x \in (0 ， 1]$ 时， $f (x) = {(\frac{1}{3})}^{1 - x}$ ，则下列判断正确的是（）

A、 $f (x)$ 的周期为2 B、 $f (2023) = - 1$ C、 $f (x + 1)$ 是偶函数 D、 $f (x)$ 的值域为 $[- 1 ， 1]$

查看试题解析
12. 已知 $O$ 是平面直角坐标系的原点，抛物线 $C ： y = \frac{1}{4} x^{2}$ 的焦点为 $F ， P ， Q$ 两点在抛物线 $C$ 上，下列说法正确的是（）

A、若 $| P F | = 5$ ，点 $P$ 的坐标为 $(4 ， 4)$ B、直线 $y = x - 1$ 与 $C$ 不相切 C、 $P$ 到直线 $y = x - 2$ 的距离的最小值为 $\frac{\sqrt{2}}{2}$ D、若 $P ， F ， Q$ 三点共线，则 $\vec{O P} \cdot \vec{O Q} = - 3$

查看试题解析

三、填空题

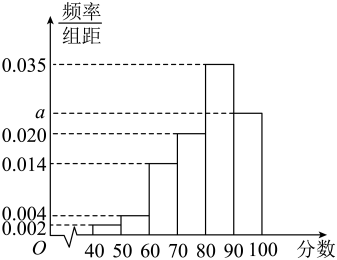
13. 某校为了了解高三年级学生的身体素质状况，在开学初举行了一场身体素质体能测试，以便对体能不达标的学生进行有针对性的训练，促进他们体能的提升，现从整个年级测试成绩中抽取100名学生的测试成绩，并把测试成绩分成 $[40 ， 50) ， [50 ， 60) ， [60 ， 70) ， [70 ， 80) ， [80 ， 90) ， [90 ， 100]$ 六组，绘制成频率分布直方图（如图所示）.其中分数在 $[90 ， 100]$ 这一组中的纵坐标为 $a$ ，则该次体能测试成绩的 $80 %$ 分位数约为分.

查看试题解析
14. 从点 $P (2 ， 3)$ 射出两条光线的方程分别为： $l_{1} ： 4 x - 3 y + 1 = 0$ 和 $l_{2} ： 3 x - 4 y + 6 = 0$ ，经 $x$ 轴反射后都与圆 $(x - a)^{2} + (y - b)^{2} = 1$ 相切，则圆的方程为.

查看试题解析
15. 已知函数 $f (x) = x - 3 l n x$ 在点 $(1 ， f (1))$ 处的切线经过点 $(a ， b) ， a > 0 ， b > 0$ ，则 $\frac{8 a + b}{a b}$ 的最小值为.

查看试题解析
16. 某工厂有甲､乙､丙三条生产线同时生产同一产品，这三条生产线生产产品的次品率分别为 $6 % ， 5 % ， 4 %$ ，假设这三条生产线产品产量的比为 $5 ： 7 ： 8$ ，现从这三条生产线上共任意选取100件产品，则次品数的数学期望为.

查看试题解析

四、解答题

17. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{5} = 5$ ， $S_{8} = 36$ ， $a_{n} = l o g_{3} (b_{n})$ .

(1)、求 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、设数列 ${c_{n}}$ 满足 $c_{n} = {\begin{array}{l} \frac{1}{a_{n} a_{n + 2}} ， n 为奇数 \\ a_{n} b_{\frac{n}{2}} ， n 为偶数 \end{array}$ ，求数列 ${c_{n}}$ 的前20项和 $T_{20}$ .

查看试题解析
18. 已知锐角三角形 $A B C$ 内角 $A ， B ， C$ 的对应边分别为 $a ， b ， c$ ，且 $c o s 2 A - \sqrt{3} s i n A + 2 = 0$ .

(1)、求 $s i n B + s i n C$ 的取值范围；

(2)、若 $a = 2 \sqrt{3}$ ，求 $△ A B C$ 的面积的最大值.

查看试题解析
19. 如图，在三棱锥 $P - A B C$ 中，底面 $△ A B C$ 是边长为4的正三角形， $P A = P C ， P B = 6$ ，三棱锥 $P - A B C$ 的体积为 $4 \sqrt{3} ， O$ 是 $A C$ 的中点， $E$ 是 $P O$ 的中点，点 $F$ 在棱 $A B$ 上，且 $A F = 3 F B$ .

(1)、求证： $E F$ $∥$ 平面 $P B C$ ；

(2)、求平面 $P A B$ 和平面 $A B C$ 所成角的余弦值.

查看试题解析
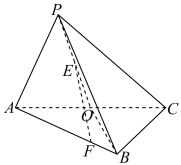20. 疫情期间某大型快餐店严格遵守禁止堂食的要求，在做好自身防护的同时，为了实现收益，也为了满足人们餐饮需求，增加打包和外卖配送服务，不仅如此，还提供了一款新套餐，丰富产品种类，该款新套餐每份成本20元，售价30元，保质期为两天，如果两天内无法售出，则过期作废，且两天内的销售情况互不影响，现统计并整理连续30天的日销量（单位：百份），得到统计数据如下表：
日销量（单位：百份）
12
13
14
15
天数
3
9
12
6

(1)、记两天中销售该款新套餐的总份数为 $X$ （单位：百份），求 $X$ 的分布列和数学期望；

(2)、以该款新套餐两天内获得利润较大为决策依据，在每两天备餐27百份､28百份两种方案中应选择哪种？

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的四个顶点围成的四边形面积为 $4 \sqrt{2}$ ，周长为 $4 \sqrt{6}$ ，一双曲线 $E$ 的顶点是该椭圆的焦点，焦点是该椭圆长轴上的顶点.

(1)、求椭圆 $C$ 和双曲线 $E$ 的标准方程；

(2)、 $A ， B ， D$ 是双曲线 $E$ 上不同的三点，且 $B ， D$ 两点关于 $y$ 轴对称， $△ A B D$ 的外接圆经过原点 $O$ .求证：直线 $A B$ 与圆 $x^{2} + y^{2} = 1$ 相切.

查看试题解析
22. 已知函数 $f (x) = e^{x} - a x ， g (x) = l n (x + 2) - a$ ，其中 $e$ 为自然对数的底数， $a \in R$ .

(1)、当 $a > 0$ 时，函数 $f (x)$ 有极小值 $f (1)$ ，求 $a$ ；

(2)、证明： $f^{'} (x) > g (x)$ 恒成立；

(3)、证明： $l n 2 + {(l n \frac{3}{2})}^{2} + {(l n \frac{4}{3})}^{3} + \dots + {(l n \frac{n + 1}{n})}^{n} < \frac{e}{e - 1}$ .

查看试题解析

日销量（单位：百份）	12	13	14	15
天数	3	9	12	6