福建省三明市普通高中2022-2023学年高二上学期数学期末质量检测试卷
试卷更新日期:2023-02-13 类型:期末考试
一、单选题
-
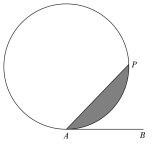
1. 抛物线的焦点坐标为( )A、 B、 C、 D、2. 直线的倾斜角的大小为( )A、30° B、60° C、120° D、150°3. 若是与的等差中项,则实数a的值为( )A、 B、 C、 D、54. 若向量 , , 且 , 则的值为( )A、 B、0 C、6 D、85. 在各项均为正数的等比数列中, , , 则( )A、16 B、 C、24 D、6. 已知A,B是抛物线上的两个动点,满足 , 其中F是C的焦点.过A,B向C的准线作垂线,垂足分别为M,N,若y轴被以MN为直径的圆E截得的线段为 , 则x轴被圆E截得的线段长为( )A、1 B、 C、2 D、7. 如图,AB是圆的切线,P是圆上的动点,设 , AP扫过的圆内阴影部分的面积S是的函数.这个函数的图象可能是( )
 A、
A、 B、
B、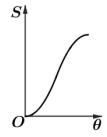 C、
C、 D、
D、 8. 如图1,北京冬奥会火种台以“承天载物”为设计理念,创意灵感来自中国传统青铜礼器——尊的曲线造型,基座沉稳,象征“地载万物”,顶部舒展开阔,寓意迎接纯洁的奥林匹克火种.如图2,一种尊的外形近似为某双曲线的一部分绕着虚轴旋转所成的曲面,尊高 , 上口直径为 , 底部直径为 , 最小直径为 , 则该双曲线的渐近线与实轴所成锐角的正切值为( )
8. 如图1,北京冬奥会火种台以“承天载物”为设计理念,创意灵感来自中国传统青铜礼器——尊的曲线造型,基座沉稳,象征“地载万物”,顶部舒展开阔,寓意迎接纯洁的奥林匹克火种.如图2,一种尊的外形近似为某双曲线的一部分绕着虚轴旋转所成的曲面,尊高 , 上口直径为 , 底部直径为 , 最小直径为 , 则该双曲线的渐近线与实轴所成锐角的正切值为( ) A、 B、 C、3 D、4
A、 B、 C、3 D、4二、多选题
-
9. 已知圆的方程为 , 以下各点在圆内的是( )A、 B、 C、 D、10. 在空间直角坐标系中,已知向量 , .以下各组值中能使得的是( )A、 , B、 , C、 , D、 ,11. 若n,m,成等比数列,则圆锥曲线的离心率可以是( )A、 B、 C、 D、212. 已知函数 , 数列满足 , 且 , .若是等差数列,则可能取的整数是( )A、 B、 C、 D、
三、填空题
-
13. 已知函数 , 则.14. 两条平行直线与间的距离为.15. 已知圆 , 圆 , 若动圆E与 , 都外切,则圆心E的轨迹方程为.16. 在数列中, , 且当时,都有.使得不等式成立的最小正整数M的值为.
四、解答题
-
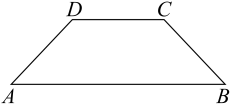
17. 如图,在四边形ABCD中, , , , , 直线AB与CD间的距离为3.建立适当的平面直角坐标系,求四边形ABCD外接圆的方程,并求该圆的圆心坐标和半径.
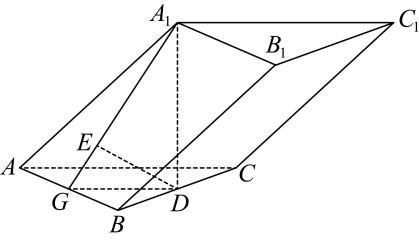
 18. 已知函数.(1)、求的导数;(2)、求曲线在点处的切线方程.19. 如图,在四面体ABCD中, , , , .
18. 已知函数.(1)、求的导数;(2)、求曲线在点处的切线方程.19. 如图,在四面体ABCD中, , , , . (1)、求的值;(2)、已知F是线段CD中点,点E满足 , 求线段EF的长.20. 在等差数列中, , 且.(1)、求数列的通项公式;(2)、已知数列的前n项和为 , 且.令 , 求数列的前n项和.
(1)、求的值;(2)、已知F是线段CD中点,点E满足 , 求线段EF的长.20. 在等差数列中, , 且.(1)、求数列的通项公式;(2)、已知数列的前n项和为 , 且.令 , 求数列的前n项和.