2023年中考数学精选真题实战测试40 菱形 B
试卷更新日期:2023-02-12 类型:二轮复习
一、单选题(每题3分,共30分)
-
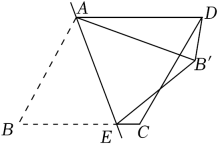
1. 关于菱形的性质,以下说法不正确的是( )A、四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形2. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )
 A、50° B、60° C、80° D、90°3. 如图,菱形 , 点、、、均在坐标轴上, , 点 , 点是的中点,点是上的一动点,则的最小值是( )
A、50° B、60° C、80° D、90°3. 如图,菱形 , 点、、、均在坐标轴上, , 点 , 点是的中点,点是上的一动点,则的最小值是( )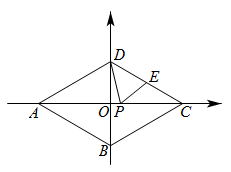 A、3 B、5 C、 D、4. 如图,四边形是菱形, , 点是中点,是对角线上一点,且 , 则的值是( )
A、3 B、5 C、 D、4. 如图,四边形是菱形, , 点是中点,是对角线上一点,且 , 则的值是( )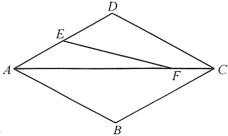 A、3 B、 C、 D、5. 如图,在菱形中,分别以、为圆心,大于为半径画弧,两弧分别交于点、 , 连接 , 若直线恰好过点与边交于点 , 连接 , 则下列结论错误的是( )
A、3 B、 C、 D、5. 如图,在菱形中,分别以、为圆心,大于为半径画弧,两弧分别交于点、 , 连接 , 若直线恰好过点与边交于点 , 连接 , 则下列结论错误的是( ) A、 B、若 , 则 C、 D、6. 如图所示,在菱形中,对角线与相交于点 , 过点作交的延长线于点 , 下列结论不一定正确的是( )
A、 B、若 , 则 C、 D、6. 如图所示,在菱形中,对角线与相交于点 , 过点作交的延长线于点 , 下列结论不一定正确的是( )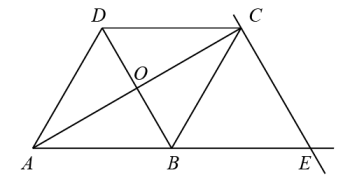 A、 B、是直角三角形 C、 D、7. 如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( )
A、 B、是直角三角形 C、 D、7. 如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( ) A、
A、 B、
B、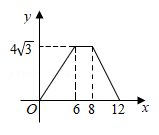 C、
C、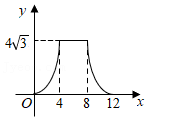 D、
D、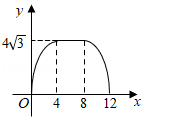 8. 如图,菱形 的对角线 与 相交于点 ,点 在 上,连接 , , , , ,则 ( )
8. 如图,菱形 的对角线 与 相交于点 ,点 在 上,连接 , , , , ,则 ( )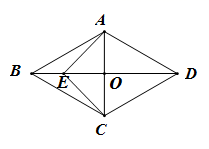 A、4 B、3 C、 D、29. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是CD中点,连接OE,则下列结论中不一定正确的是( )
A、4 B、3 C、 D、29. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是CD中点,连接OE,则下列结论中不一定正确的是( )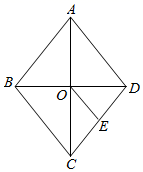 A、AB=AD B、OE AB C、∠DOE=∠DEO D、∠EOD=∠EDO10. 如图,在菱形ABCD中, ,点E,F分別在边AB,BC上, , 的周长为 ,则AD的长为( )
A、AB=AD B、OE AB C、∠DOE=∠DEO D、∠EOD=∠EDO10. 如图,在菱形ABCD中, ,点E,F分別在边AB,BC上, , 的周长为 ,则AD的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
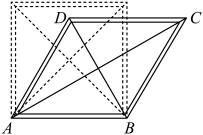
11. 如图,将一个边长为的正方形活动框架(边框粗细忽略不计)扭动成四边形 , 对角线是两根橡皮筋,其拉伸长度达到时才会断裂.若 , 则橡皮筋断裂(填“会”或“不会”,参考数据:).
 12. 如图,在四边形ABCD中,AC⊥BD,垂足为O, , 要使四边形ABCD为菱形,应添加的条件是 . (只需写出一个条件即可)
12. 如图,在四边形ABCD中,AC⊥BD,垂足为O, , 要使四边形ABCD为菱形,应添加的条件是 . (只需写出一个条件即可)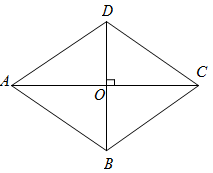 13. 如图,BD是菱形ABCD的一条对角线,点E在BC的延长线上,若 ,则 的度数为度.
13. 如图,BD是菱形ABCD的一条对角线,点E在BC的延长线上,若 ,则 的度数为度. 14. 如图,在菱形 中, ,对角线 、 相交于点 ,点 在线段 上,且 ,点 为线段 上的一个动点,则 的最小值是.
14. 如图,在菱形 中, ,对角线 、 相交于点 ,点 在线段 上,且 ,点 为线段 上的一个动点,则 的最小值是. 15. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)
15. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)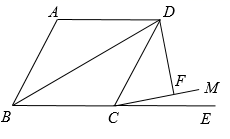 16. 如图,在菱形中,.若M、N分别是边上的动点,且 , 作 , 垂足分别为E、F,则的值为.
16. 如图,在菱形中,.若M、N分别是边上的动点,且 , 作 , 垂足分别为E、F,则的值为.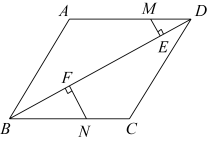
三、解答题(共8题,共72分)
-
17. 如图,在中,对角线AC,BD相交于点O,.
 (1)、求证:;(2)、若点E,F分别为AD,AO的中点,连接EF, , 求BD的长及四边形ABCD的周长.18. 如图,在四边形ABCD中,ABCD,AC平分∠DAB,AB=2CD,E为AB中点,连接CE.
(1)、求证:;(2)、若点E,F分别为AD,AO的中点,连接EF, , 求BD的长及四边形ABCD的周长.18. 如图,在四边形ABCD中,ABCD,AC平分∠DAB,AB=2CD,E为AB中点,连接CE.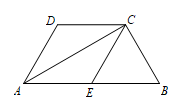 (1)、求证:四边形AECD为菱形;(2)、若∠D=120°,DC=2,求△ABC的面积.19. 如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是AD的中点,连接OE,过点D作DF∥AC交OE的延长线于点F,连接AF.
(1)、求证:四边形AECD为菱形;(2)、若∠D=120°,DC=2,求△ABC的面积.19. 如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是AD的中点,连接OE,过点D作DF∥AC交OE的延长线于点F,连接AF. (1)、求证:△AOE≌△DFE;(2)、判定四边形AODF的形状并说明理由.20. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)、求证:△AOE≌△DFE;(2)、判定四边形AODF的形状并说明理由.20. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.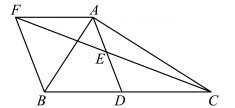 (1)、求证:四边形ADBF是菱形;(2)、若AB=8,菱形ADBF的面积为40,求AC的长.21. 如图,在菱形ABCD中,∠BAD = 120°,AB = 6,连接BD .
(1)、求证:四边形ADBF是菱形;(2)、若AB=8,菱形ADBF的面积为40,求AC的长.21. 如图,在菱形ABCD中,∠BAD = 120°,AB = 6,连接BD . (1)、求BD的长;(2)、点E为线段BD上一动点(不与点B,D重合), 点F在边AD上,且BE=DF,
(1)、求BD的长;(2)、点E为线段BD上一动点(不与点B,D重合), 点F在边AD上,且BE=DF,①当CE丄AB时,求四边形ABEF的面积;
②当四边形ABEF的面积取得最小值时,CE+CF的值是否也最小?如果是,求CE+CF的最小值;如果不是,请说明理由.
22. 已知菱形 中, 是边 的中点, 是边 上一点.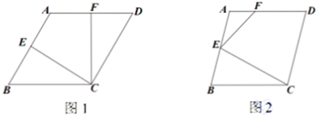 (1)、如图1,连接 , . , .
(1)、如图1,连接 , . , .①求证: ;
②若 ,求 的长;
(2)、如图2,连接 , .若 , ,求 的长.23. 已知四边形ABCD中,BC=CD.连接BD,过点C作BD的垂线交AB于点E,连接DE. (1)、如图1,若 , 求证:四边形BCDE是菱形;(2)、如图2,连接AC,设BD,AC相交于点F,DE垂直平分线段AC.
(1)、如图1,若 , 求证:四边形BCDE是菱形;(2)、如图2,连接AC,设BD,AC相交于点F,DE垂直平分线段AC.(ⅰ)求∠CED的大小;
(ⅱ)若AF=AE,求证:BE=CF.
24. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .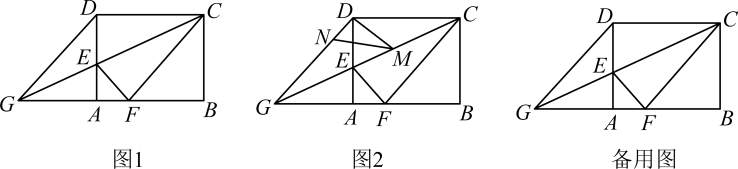 (1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.
(1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.