2023年中考数学精选真题实战测试39 菱形 A
试卷更新日期:2023-02-11 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
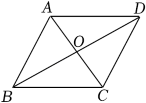 A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形2. 如图,在菱形中,分别以、为圆心,大于为半径画弧,两弧分别交于点、 , 连接 , 若直线恰好过点与边交于点 , 连接 , 则下列结论错误的是( )
A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形2. 如图,在菱形中,分别以、为圆心,大于为半径画弧,两弧分别交于点、 , 连接 , 若直线恰好过点与边交于点 , 连接 , 则下列结论错误的是( ) A、 B、若 , 则 C、 D、3. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )
A、 B、若 , 则 C、 D、3. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )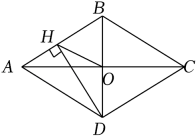 A、4 B、4 C、8 D、84. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A、4 B、4 C、8 D、84. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )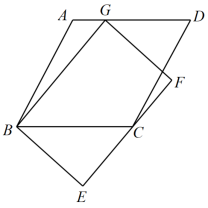 A、 B、 C、 D、35. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( )
A、 B、 C、 D、35. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( ) A、 B、 C、 D、6. 如图,菱形中,点E是边的中点,垂直交的延长线于点F,若 , 则菱形的边长是( )
A、 B、 C、 D、6. 如图,菱形中,点E是边的中点,垂直交的延长线于点F,若 , 则菱形的边长是( )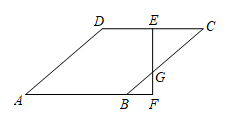 A、3 B、4 C、5 D、7. 如图1,在菱形 中, ,动点 从点 出发,沿折线 方向匀速运动,运动到点 停止.设点 的运动路程为 , 的面积为 , 与 的函数图象如图2所示,则 的长为( )
A、3 B、4 C、5 D、7. 如图1,在菱形 中, ,动点 从点 出发,沿折线 方向匀速运动,运动到点 停止.设点 的运动路程为 , 的面积为 , 与 的函数图象如图2所示,则 的长为( )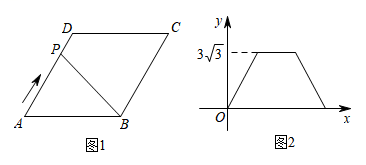 A、 B、 C、 D、8. 如图,已知菱形ABCD的边长为4,E是BC的中点,AF平分∠EAD交CD于点F,FG∥AD交AE于点G,若cosB= ,则FG的长是( )
A、 B、 C、 D、8. 如图,已知菱形ABCD的边长为4,E是BC的中点,AF平分∠EAD交CD于点F,FG∥AD交AE于点G,若cosB= ,则FG的长是( )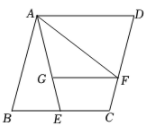 A、3 B、 C、 D、9. 如图,菱形 ABCD 对角线交点与坐标原点 O 重合,点 A(-2,5) ,则点C的坐标为( )
A、3 B、 C、 D、9. 如图,菱形 ABCD 对角线交点与坐标原点 O 重合,点 A(-2,5) ,则点C的坐标为( )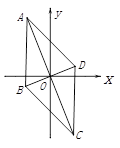 A、 B、 C、 D、10. 如图,在边长为1的菱形中, , 动点E在边上(与点A、B均不重合),点F在对角线上,与相交于点G,连接 , 若 , 则下列结论错误的是( )
A、 B、 C、 D、10. 如图,在边长为1的菱形中, , 动点E在边上(与点A、B均不重合),点F在对角线上,与相交于点G,连接 , 若 , 则下列结论错误的是( ) A、 B、 C、 D、的最小值为
A、 B、 C、 D、的最小值为二、填空题(每空3分,共18分)
-
11. 已知菱形的对角线相交于点 , , , 则菱形的面积为.12. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .
 13. 如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF= , 则BD的长为(结果保留很号).
13. 如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF= , 则BD的长为(结果保留很号).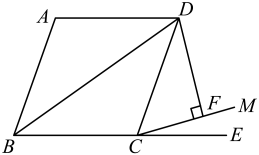 14. 菱形的边长为2, , 点、分别是、上的动点,的最小值为.
14. 菱形的边长为2, , 点、分别是、上的动点,的最小值为.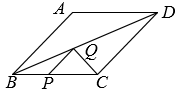 15. 如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是 (限填序号).
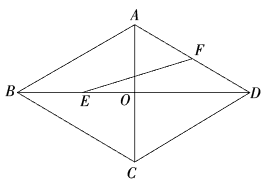
15. 如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是 (限填序号).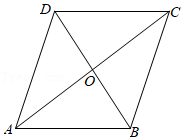 16. 如图,四边形ABCD是边长为6的菱形,∠ABC=60°,对角线AC与BD交于点O,点E,F分别是线段AB,AC上的动点(不与端点重合),且BE=AF,BF与CE交于点P,延长BF交边AD(或边CD)于点G,连接OP,OG,则下列结论:①△ABF≌△BCE;②当BE=2时,△BOG的面积与四边形OCDG面积之比为1:3;③当BE=4时,BE:CG=2:1;④线段OP的最小值为2﹣2 . 其中正确的是 . (请填写序号)
16. 如图,四边形ABCD是边长为6的菱形,∠ABC=60°,对角线AC与BD交于点O,点E,F分别是线段AB,AC上的动点(不与端点重合),且BE=AF,BF与CE交于点P,延长BF交边AD(或边CD)于点G,连接OP,OG,则下列结论:①△ABF≌△BCE;②当BE=2时,△BOG的面积与四边形OCDG面积之比为1:3;③当BE=4时,BE:CG=2:1;④线段OP的最小值为2﹣2 . 其中正确的是 . (请填写序号)
三、解答题(共8题,共72分)
-
17. 如图,四边形中,ABDC, , 于点 .
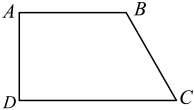 (1)、用尺规作的角平分线,交于点;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形是菱形.18. 如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F.
(1)、用尺规作的角平分线,交于点;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形是菱形.18. 如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F.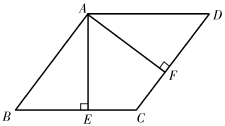 (1)、求证:△ABE≌△ADF;(2)、若AE=4,CF=2,求菱形的边长.19. 如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与点A,C重合),连接DE并延长交射线AB于点F,连接BE.
(1)、求证:△ABE≌△ADF;(2)、若AE=4,CF=2,求菱形的边长.19. 如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与点A,C重合),连接DE并延长交射线AB于点F,连接BE. (1)、求证:;(2)、求证: .20. 如图,在Rt中, , . 点D是的中点,过点D作交于点E.延长至点F,使得 , 连接、、 .
(1)、求证:;(2)、求证: .20. 如图,在Rt中, , . 点D是的中点,过点D作交于点E.延长至点F,使得 , 连接、、 . (1)、求证:四边形是菱形;(2)、若 , 则的值为 .21. 如图,在矩形 中, ,点E是 边上的任一点(不包括端点D,C),过点A作 交 的延长线于点F,设 .
(1)、求证:四边形是菱形;(2)、若 , 则的值为 .21. 如图,在矩形 中, ,点E是 边上的任一点(不包括端点D,C),过点A作 交 的延长线于点F,设 .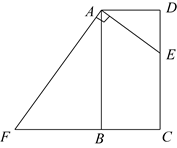 (1)、求 的长(用含a的代数式表示);(2)、连接 交 于点G,连接 ,当 时,求证:四边形 是菱形.22. 如图,点 , 分别在的边 , 上, , 连接 , .请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形.
(1)、求 的长(用含a的代数式表示);(2)、连接 交 于点G,连接 ,当 时,求证:四边形 是菱形.22. 如图,点 , 分别在的边 , 上, , 连接 , .请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形.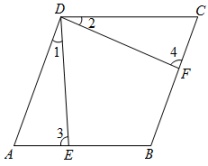 (1)、你添加的条件是(填序号);(2)、添加了条件后,请证明为菱形.23. 在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图(1),在菱形中,为锐角,为中点,连接 , 将菱形沿折叠,得到四边形 , 点的对应点为点 , 点的对应点为点.
(1)、你添加的条件是(填序号);(2)、添加了条件后,请证明为菱形.23. 在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图(1),在菱形中,为锐角,为中点,连接 , 将菱形沿折叠,得到四边形 , 点的对应点为点 , 点的对应点为点.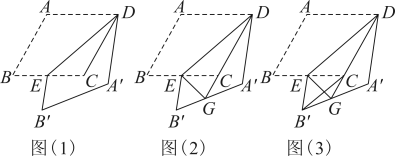 (1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.24. 已知 , AB=AC,AB>BC.
(1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.24. 已知 , AB=AC,AB>BC.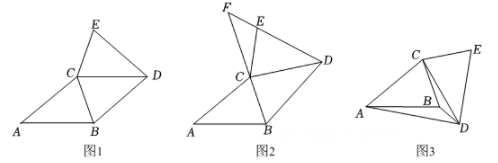 (1)、如图1,CB平分∠ACD,求证:四边形ABDC是菱形;(2)、如图2,将(1)中的△CDE绕点C逆时针旋转(旋转角小于∠BAC),BC,DE的延长线相交于点F,用等式表示∠ACE与∠EFC之间的数量关系,并证明;(3)、如图3,将(1)中的△CDE绕点C顺时针旋转(旋转角小于∠ABC),若 , 求∠ADB的度数.
(1)、如图1,CB平分∠ACD,求证:四边形ABDC是菱形;(2)、如图2,将(1)中的△CDE绕点C逆时针旋转(旋转角小于∠BAC),BC,DE的延长线相交于点F,用等式表示∠ACE与∠EFC之间的数量关系,并证明;(3)、如图3,将(1)中的△CDE绕点C顺时针旋转(旋转角小于∠ABC),若 , 求∠ADB的度数.