人教版八年级下数学疑难点专题专练——勾股定理逆定理最短路径相关
试卷更新日期:2023-02-11 类型:同步测试
一、单选题
-
1.
如图,矩形ABCD中,AB=4,BC=3,若在AC,AB上各取一点M,N,使BM+MN的值最小,求这个最小值( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
2. 如图,中, , , , 是的中点,是上一动点,则的最小值为.
 3. 如图,在中, , , 是的平分线,.若 , 分别是和上的动点,则的最小值是.
3. 如图,在中, , , 是的平分线,.若 , 分别是和上的动点,则的最小值是. 4. 如图,点B在射线AN上,以为边作等边 , M为中点,且 , P为中点,当最小时, .
4. 如图,点B在射线AN上,以为边作等边 , M为中点,且 , P为中点,当最小时, . 5. 如图,中, , , , 点为边上的动点,过点作于点 , 则的最小值为.
5. 如图,中, , , , 点为边上的动点,过点作于点 , 则的最小值为. 6. 如图,在中, , , , 点P是线段上一动点,点M在线段上,当时,的最小值为 .
6. 如图,在中, , , , 点P是线段上一动点,点M在线段上,当时,的最小值为 . 7. 如图,等腰Rt△ABC的直角边长为4,D、E分别为边AB、AC上两个动点,且AE=BD,则CD+BE的最小值.
7. 如图,等腰Rt△ABC的直角边长为4,D、E分别为边AB、AC上两个动点,且AE=BD,则CD+BE的最小值. 8. 如图,在四边形ABCD中,∠A=90°,AD∥BC,AB=4,点P是线段AD上的动点,连接BP,CP,若△BPC周长的最小值为16,则BC的长为.
8. 如图,在四边形ABCD中,∠A=90°,AD∥BC,AB=4,点P是线段AD上的动点,连接BP,CP,若△BPC周长的最小值为16,则BC的长为. 9. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为.
9. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为. 10. 如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为 .
10. 如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为 . 11. 如图所示,中, , , , 是的角平分线,若、分别是和上的动点,则的最小值是 .
11. 如图所示,中, , , , 是的角平分线,若、分别是和上的动点,则的最小值是 . 12. 如图,在平面直角坐标系中,△OAB为等边三角形,AB丄x轴,AB=2,点C的坐标为(1,0),点P为OB边上的一个动点,则PA+PC的最小值为 .
12. 如图,在平面直角坐标系中,△OAB为等边三角形,AB丄x轴,AB=2,点C的坐标为(1,0),点P为OB边上的一个动点,则PA+PC的最小值为 . 13. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 .
13. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 .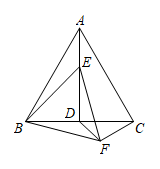 14. 如图,在中, , , , 平分交于点D,点E、F分别在、上,则的最小值为 .
14. 如图,在中, , , , 平分交于点D,点E、F分别在、上,则的最小值为 .
三、综合题
-

