广东省中山市2022-2023学年九年级上学期数学期末试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
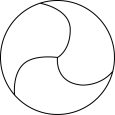 B、
B、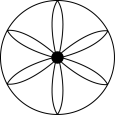 C、
C、 D、
D、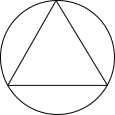 2. 拋物线的顶点坐标是( )A、 B、 C、 D、3. 方程的根是( )A、 , B、 , C、 , D、 ,4. 已知关于的一元二次方程 , 下列说法正确的是( )A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、方程没有实数根 D、方程的根为 ,5. 下列事件中,必然发生的事件是( )A、从一个班级中任选13人,至少有两人的出生月份相同 B、中山市近三天会下雨 C、车开到一个十字路口,遇到绿灯 D、从广州南站到中山站的动车明天正点到达中山站6. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
2. 拋物线的顶点坐标是( )A、 B、 C、 D、3. 方程的根是( )A、 , B、 , C、 , D、 ,4. 已知关于的一元二次方程 , 下列说法正确的是( )A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、方程没有实数根 D、方程的根为 ,5. 下列事件中,必然发生的事件是( )A、从一个班级中任选13人,至少有两人的出生月份相同 B、中山市近三天会下雨 C、车开到一个十字路口,遇到绿灯 D、从广州南站到中山站的动车明天正点到达中山站6. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )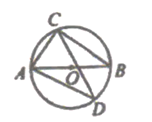 A、35° B、45° C、55° D、65°7. 如图,用力转动转盘甲和转盘乙的指针,则哪个转盘的指针停在白色区域的概率大( )
A、35° B、45° C、55° D、65°7. 如图,用力转动转盘甲和转盘乙的指针,则哪个转盘的指针停在白色区域的概率大( ) A、转盘甲 B、转盘乙 C、无法确定 D、一样大8. 如图,在中, , , 则图中阴影部分的面积为( )
A、转盘甲 B、转盘乙 C、无法确定 D、一样大8. 如图,在中, , , 则图中阴影部分的面积为( ) A、 B、 C、 D、9. 从底面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:h=30t-5t2 , 这个函数图象如图所示,则小球从第3s到第5s的运动路径长为( )
A、 B、 C、 D、9. 从底面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:h=30t-5t2 , 这个函数图象如图所示,则小球从第3s到第5s的运动路径长为( ) A、15m B、20m C、25m D、30m10. 点是内一点,过点的最长弦的长为10,最短弦的长为6,则的长为( )A、8 B、2 C、5 D、4
A、15m B、20m C、25m D、30m10. 点是内一点,过点的最长弦的长为10,最短弦的长为6,则的长为( )A、8 B、2 C、5 D、4二、填空题
-
11. 关于x的一元二次方程有一个根是 , 则 .12. 若点与点B关于原点对称,则点B的坐标为 .13. 已知的半径为6,则的内接正方形的边长为 .14. 在一个不透明的盒子里装有除颜色不同外其余均相同的黑、白两种球,其中黑球有5个.将盒子里的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系如图所示,经分析可以推断盒子里白球有.
 15. 如图,在中, , 点是的内心,则度.
15. 如图,在中, , 点是的内心,则度.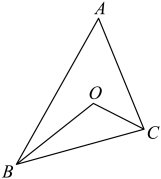
三、解答题
-
16. 解方程: .17. 求函数的最值,并说明是最大值还是最小值.18. 一个鞋柜里放有一双白色运动鞋和一双黑色皮鞋,如果从中随机取出2只鞋子,求取出的鞋子是同一双的概率.19. 如图,的直径 , 、是圆上的两点, , , 求 , 两点的距离.
 20. 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
20. 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.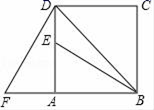 (1)、指出旋转中心和旋转角度;(2)、求DE的长度和∠EBD的度数.21. 如图,矩形是一块长米、宽米的荒地,要在这块荒地上建造一个矩形花园 , 在花园的外围是宽度相等的小路.要使花园所占面积为荒地面积的一半,则小路的宽为多少米?
(1)、指出旋转中心和旋转角度;(2)、求DE的长度和∠EBD的度数.21. 如图,矩形是一块长米、宽米的荒地,要在这块荒地上建造一个矩形花园 , 在花园的外围是宽度相等的小路.要使花园所占面积为荒地面积的一半,则小路的宽为多少米?