山西省朔州市右玉县2022-2023学年八年级上学期期末考试数学试卷

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. 已知某细菌直径长约0.0000202米，那么该细菌的直径长用科学记数法可表示为（）

A、 $2.02 \times 1 0^{- 4}$ 米 B、 $2.02 \times 1 0^{4}$ 米 C、 $2.02 \times 1 0^{5}$ 米 D、 $2.02 \times 1 0^{- 5}$ 米

查看试题解析
2. 下列运算正确的是（）

A、 $2 x + 3 y = 5 x y$ B、 ${(x - 3)}^{2} = x^{2} - 9$ C、 ${(- 2 a^{3} b^{2})}^{3} = - 8 a^{9} b^{6}$ D、 $x^{6} \div x^{3} = x^{2}$

查看试题解析
3. 如图，直线l₁、l₂、l₃表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（）

A、1处 B、2处 C、3处 D、4处

查看试题解析
4. 点 $A (a - 8 ， 3)$ ，点 $B (2 ， b + 3)$ 关于 $x$ 轴对称，则 $a + b$ 的平方根为（）

A、1 B、2 C、 $\pm 2$ D、 $\pm 1$

查看试题解析
5. 下列分式是最简分式的是（）

A、 $\frac{3 m + 2}{m}$ B、 $\frac{- 10 m n^{2}}{5 m n}$ C、 $\frac{m^{2} - m}{m - 1}$ D、 $\frac{m + 2}{m^{2} - 4}$

查看试题解析
6. 已知，如图， $△ A B C$ 中， $A B = A C$ ， $∠ A = 120 °$ ， $B C = 12 c m$ ， $A B$ 的垂直平分线交 $B C$ 于点M，交 $A B$ 于点E， $A C$ 的垂直平分线交 $B C$ 于点N，交 $A C$ 于点F，则 $M N$ 的长为（）

A、3cm B、4cm C、6cm D、12cm

查看试题解析
7. 已知 $4 x^{2} - 2 (k - 1) x + 1$ 是一个完全平方式，则k的值为（）

A、 $\pm 2$ B、2 C、1或－3 D、－1或3

查看试题解析
8. 已知等腰三角形一腰上的高与另一腰的夹角为 $35 °$ ，那么这个等腰三角形的顶角等于（）

A、 $55 °$ 或 $125 °$ B、 $55 °$ C、 $125 °$ D、 $35 °$ 或 $55 °$

查看试题解析
9. 如图，△ABC中，∠ABC、∠FCA的角平分线BP、CP交于点P，延长BA、BC，PM⊥BE于M，PN⊥BF于N，则下列结论：①AP平分∠EAC；② $∠ A B C + 2 ∠ A P C = 180 °$ ；③ $∠ B A C = 2 ∠ B P C$ ；④ $S_{Δ P A C} = S_{Δ M A P} + S_{Δ N C P}$ ．其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 有一个数值转换器，原理如图所示，若开始输入x的值是5，可发现第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是4.依次继续下去，第2022次输出的结果是（）

A、8 B、4 C、2 D、1

查看试题解析

二、填空题

11. 当x=时，分式 $\frac{x^{2} - 1}{x - 1}$ 值为0．

查看试题解析
12. 因式分解： $a^{2} (x - y) + (y - x) =$ ．

查看试题解析
13. 已知 $3^{a} = 10$ ， $9^{b} = 8$ ，则 $3^{a - 2 b}$ 的值为．

查看试题解析
14. 计算： ${(3 x^{- 3} y)}^{- 2} \div {(x^{2} y^{- 3})}^{- 2} =$ ．

查看试题解析
15. 如图，已知点P是射线 $M N$ 上一动点， $∠ A M N = 35 °$ ，当 $∠ A$ 为时， $△ A M P$ 是等腰三角形．

查看试题解析

三、解答题

16. 计算：

(1)、 $- 1^{2} - {(- 2)}^{3} \div 4 + {(\frac{1}{2})}^{- 2} - | - 2 | + {(3 - π)}^{0}$ ．

(2)、 $(3 x + 2) (3 x - 2) - 5 x (x - 1) - {(2 x - 1)}^{2}$

查看试题解析
17. 先化简，再求值： $\frac{2}{a - 3} + \frac{a}{a^{2} - 9} \div \frac{a^{2} - 4 a}{a + 3}$ ，其中a，2，4为 $△ A B C$ 的三边长，且a为整数．

查看试题解析
18. 如图，在 $10 \times 10$ 网格中，每个小正方形的边长都为1．

( 1 )建立如图所示的平面直角坐标系，若点 $A (3 ， 4)$ ，则点C的坐标____；

( 2 )将 $Δ A O C$ 向左平移5个单位，向上平移2个单位，则点C的坐标变为____；（无需画图）

( 3 )图中格点 $Δ A O C$ 的面积是____；

( 4 )在x轴上找一点P，使得 $P A + P C$ 最小，请画出点P的位置．

查看试题解析
19. 已知关于x的方程 $\frac{2 x}{x - 2} + \frac{m}{x - 2} = - 2$

(1)、当 $m = 5$ 时，求方程的解；

(2)、当m取何值时，此方程无解；

(3)、当此方程的解是正数时，求m的取值范围．

查看试题解析
20. 如图，在等边 $△ A B C$ 中，点D，E分别在边 $A C ， A B$ 上，且 $A D = B E$ ， $B D ， C E$ 交于点P， $C F ⊥ B D$ ，垂足为点F．

(1)、求证： $B D = C E$ ；

(2)、若 $C P = 7$ ，求 $P F$ 的长．

查看试题解析
21. 某服装店到厂家选购A、B两种品牌的儿童服装，每套A品牌服装进价比B品牌服装每套进价多 $20$ 元，已知用 $2000$ 元购进A种服装的数量是用 $750$ 元购进B种服装数量的2倍．

(1)、求A、B两种品牌服装每套进价分别为多少元？

(2)、若A品牌服装每套售价为 $130$ 元，B品牌服装每套售价为 $95$ 元，服装店老板决定，购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套，两种服装全部售出后，要使总利润不少于 $1200$ 元，则最少购进A品牌的服装多少套？

查看试题解析
22. 【阅读理解】
“若x满足 $(80 - x) (x - 60) = 30$ ，求 ${(80 - x)}^{2} + {(x - 60)}^{2}$ 的值”
解：设 $(80 - x) = a$ ， $(x - 60) = b$ ，则 $(80 - x) (x - 60) = a b = 30$ ， $a + b = (80 - x) + (x - 60) = 20$ ，所以 ${(80 - x)}^{2} + {(x - 60)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 2 0^{2} - 2 \times 30 = 340$
【解决问题】

(1)、若x满足 $(25 - x) (18 - x) = 30$ ，求 ${(25 - x)}^{2} + {(18 - x)}^{2}$ 的值．

(2)、若x满足 $x^{2} + {(10 - x)}^{2} = 260$ ，求 $x (10 - x)$ 的值．

(3)、如图，正方形ABCD的边长为x， $A E = 6$ ， $C G = 8$ ，长方形EFGD的面积是240，四边形NGDH和MEDQ都是正方形，PQDH是长方形，求图中阴影部分的面积（结果必须是一个具体的数值）．

查看试题解析
23. 如图1，在平面直角坐标系中，点A在y轴上，点B在x轴上，以AB为边作等腰直角三角形ABC，使 $A B = A C$ ， $∠ B A C = 90 °$ ，点C在第二象限．

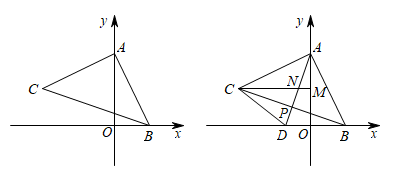(1)、若点 $A (0 ， a)$ ， $B (b ， 0)$ ，且a、b满足 $\sqrt{a - 6} + b^{2} - 6 b + 9 = 0$ ，则 $a =$ ， $b =$ ，点C的坐标为；

(2)、如图2，过点C作 $C M ⊥ y$ 轴于点M，AD平分∠BAC，交x轴于点D，交CM于点N，交BC于点P，求证：CP垂直平分DN；

(3)、试探究（2）中OM，OD与MN之间的关系，并说明理由．

查看试题解析