山西省临汾市2022-2023学年八年级上学期期末数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列四个实数中,是无理数的是( )A、 B、 C、 D、2. 下列运算结果正确的是( )A、 B、 C、 D、3. 如图,在中, , 点P为内一点,连接、、 , , 求证: , 用反证法证明时,第一步应假设( )
 A、 B、 C、 D、4. 如下是某地区2022年12月12~21日每天最高气温的统计表:
A、 B、 C、 D、4. 如下是某地区2022年12月12~21日每天最高气温的统计表:日期
12月12日
12月13日
12月14日
12月15日
12月16日
最高气温
日期
12月17日
12月18日
12月19日
12月20日
12月21日
最高气温
在这天中,最高气温为出现的频率是( )
A、 B、 C、 D、5. 如图,阴影部分是在一个边长为的大正方形中剪去一个边长为的小正方形后得到的图形,将阴影部分通过割、拼,形成新的图形.给出下列四种割拼方法,每种割拼方法都能够验证平方差公式,其中用到的数学思想是( )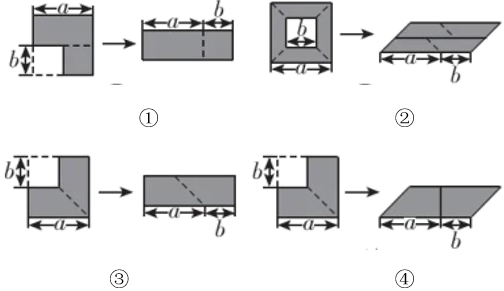 A、数形结合思想 B、分类思想 C、公理化思想 D、函数思想6. 2022年2月28日,国家统计局发布《中华人民共和国2021年国民经济和社会发展统计公报》(简称《公报》).如图所示是《公报》中显示的“2017-2021年社会消费品零售总额及其增长速度”的统计图,根据统计图得出如下结论,其中正确的是( )
A、数形结合思想 B、分类思想 C、公理化思想 D、函数思想6. 2022年2月28日,国家统计局发布《中华人民共和国2021年国民经济和社会发展统计公报》(简称《公报》).如图所示是《公报》中显示的“2017-2021年社会消费品零售总额及其增长速度”的统计图,根据统计图得出如下结论,其中正确的是( ) A、2017-2021年期间社会消费品零售总额逐年增长 B、2017-2021年期间社会消费品零售总额先减后增 C、2017-2021年期间2017年社会消费品零售总额比上年增长率最低 D、2017-2021年期间2021年社会消费品零售总额比上年增长率最高7. 若 ,则 的值是( )A、 B、 C、 D、8. 小华同学周末在家做家务,不慎把家里的一块三角形玻璃打碎成如图所示的四块,现在要去玻璃店配一块完全一样的玻璃,可以选择的方法是( )
A、2017-2021年期间社会消费品零售总额逐年增长 B、2017-2021年期间社会消费品零售总额先减后增 C、2017-2021年期间2017年社会消费品零售总额比上年增长率最低 D、2017-2021年期间2021年社会消费品零售总额比上年增长率最高7. 若 ,则 的值是( )A、 B、 C、 D、8. 小华同学周末在家做家务,不慎把家里的一块三角形玻璃打碎成如图所示的四块,现在要去玻璃店配一块完全一样的玻璃,可以选择的方法是( ) A、带①②去 B、带②③去 C、带③④去 D、带②④去9. 已知在中, , , 的对边分别记为 , , , 则下列条件不能判定为直角三角形的是( )A、 B、 C、 D、10. 如图,在中,的平分线交于点D,过点D分别作 , , 垂足分别为E,F,连接 . 有下列四个结论:①;②垂直平分;③;④ . 其中一定正确的是( )
A、带①②去 B、带②③去 C、带③④去 D、带②④去9. 已知在中, , , 的对边分别记为 , , , 则下列条件不能判定为直角三角形的是( )A、 B、 C、 D、10. 如图,在中,的平分线交于点D,过点D分别作 , , 垂足分别为E,F,连接 . 有下列四个结论:①;②垂直平分;③;④ . 其中一定正确的是( ) A、①②③ B、①③④ C、①②④ D、②③④
A、①②③ B、①③④ C、①②④ D、②③④二、填空题
-
11. 若a+b=3,ab=2,则a2+b2= .12. 命题“等腰三角形的两个底角相等.”的逆命题是 .13. 喜欢探索数学知识的小明遇到一个新的定义:对于三个正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个正整数为“和谐组合”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”.例如1,4,9这三个数, , , , 其结果都是整数,所以1,4.9三个数称为“和谐组合”,其中最小算术平方根是2,最大算术平方根是6.若2,8,18三个数是“和谐组合”,则其中最小算术平方根与最大算术平方根的和是 .14. 如图,在中, , D,E,F分别是边 , , 上的点,且 , . 若 , 则的度数为°.
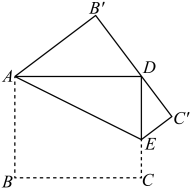
 15. 如图,有一张长方形片ABCD , , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
15. 如图,有一张长方形片ABCD , , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
三、解答题
-
16.(1)、分解因式::(2)、先化简,再求值: , 其中 , .17. 如图,网格中每个小正方形的边长都是1,点A、B、C、D都在格点上.
 (1)、线段AB的长度是 , 线段CD的长度是 .(2)、若EF的长为 , 那么以AB、CD、EF三条线段为边能否构成直角三角形,并说明理由.18. 如图,是等边三角形,D是AC边的中点,延长BC至点E,使 .
(1)、线段AB的长度是 , 线段CD的长度是 .(2)、若EF的长为 , 那么以AB、CD、EF三条线段为边能否构成直角三角形,并说明理由.18. 如图,是等边三角形,D是AC边的中点,延长BC至点E,使 . (1)、利用尺规作的平分线 , 交于点M.(要求:保留作图痕迹,不写作法,标明字母)(2)、求的度数.19. 材料:常见的分解因式的方法有提公因式法和公式法,而有的多项式既没有公因式,也不能直接运用公式分解因式,但是某些项通过适当的调整能构成可分解的一组,用分组来分解一个多项式的因式,这种方法叫做分组分解法.如 , 我们仔细观察这个式子会发现,前三项符合完全平方公式,分解后与后面的部分结合起来又符合平方差公式,可以继续分解,过程为 . 它并不是一种独立的分解因式的方法,而是为提公因式或运用公式分解因式创造条件.
(1)、利用尺规作的平分线 , 交于点M.(要求:保留作图痕迹,不写作法,标明字母)(2)、求的度数.19. 材料:常见的分解因式的方法有提公因式法和公式法,而有的多项式既没有公因式,也不能直接运用公式分解因式,但是某些项通过适当的调整能构成可分解的一组,用分组来分解一个多项式的因式,这种方法叫做分组分解法.如 , 我们仔细观察这个式子会发现,前三项符合完全平方公式,分解后与后面的部分结合起来又符合平方差公式,可以继续分解,过程为 . 它并不是一种独立的分解因式的方法,而是为提公因式或运用公式分解因式创造条件.解答下列问题:
(1)、分解因式:;(2)、请尝试用上面材料中的方法分解因式 .20. 国际足联世界杯(FIFA World Cup),简称“世界杯”,是由全世界国家级别球队参与,象征足球界最高荣誉,并具有最高知名度和最大影响力的足球赛事.世界杯每四年举办一次,任何国际足联会员国(地区)都可以派出代表队报名参加这项赛事.第22届世界杯足球赛在卡塔尔举行,为了解同学们对卡塔尔世界杯的了解情况,某数学兴趣小组利用课余时间在全校抽取了部分学生进行问卷调查,将调查结果分为四个等级(A.不了解;B.了解较少;C.了解较多;D.十分了解)进行统计,并将统计结果绘制成如下两幅不完整的统计图:
请你根据统计图提供的信息,解答下列问题:
(1)、求被调查的学生总人数.(2)、补全条形统计图与扇形统计图.(3)、在扇形统计图中,表示“C”所在的扇形圆心角的度数为°.(4)、从以上统计图中你能得出什么结论?说说你的想法.(写出一条即可)21. 如图,某火车站内部墙面上有破损处(看作点A),现维修师傅需借助梯子完成维修工作.梯子的长度为 , 将其斜靠在这面墙上,测得梯子底部E离墙角N处 , 维修师傅爬到梯子顶部使用仪器测量,此时梯子顶部D距离墙面破损处 . (1)、该火车站墙面破损处A距离地面有多高?(2)、如果维修师傅要使梯子顶部到地面的距离为4.8m.那么梯子底部需要向墙角方向移动多少米?22. 综合与实践
(1)、该火车站墙面破损处A距离地面有多高?(2)、如果维修师傅要使梯子顶部到地面的距离为4.8m.那么梯子底部需要向墙角方向移动多少米?22. 综合与实践在等腰三角形纸片中, , . 现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).下面是小文借助尺规解决这一问题的过程,请阅读后完成相应的任务.
作法:如图1.
①分别作 , 的垂直平分线,交于点P;
②连接 , ,
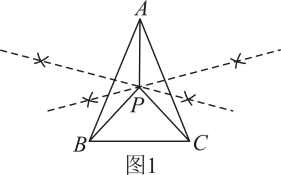
结论:沿线段 , , 剪开,即可得到三个等腰三角形
理由:∵点P在线段的垂直平分线上,
∴____.(依据)
同理,得
∴
∴ , , 都是等腰三角形.
任务:
(1)、上述过程中,横线上的结论为 , 括号中的依据为 .(2)、受小文的启发,同学们想到另一种思路:如图2,以点B为圆心,长为半径作弧,交于点D,交于点E.在此基础上构造两条线段(以图中标有字母的点为端点)作为裁剪线,也可解决问题.请在图2中画出一种裁剪方案,并求出得到的三个等腰三角形及相应顶角的度数. (3)、如图3,在等腰三角形纸片中, , . 请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形.(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线)
(3)、如图3,在等腰三角形纸片中, , . 请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形.(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线) 23. 在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC=∠BAC=α.
23. 在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC=∠BAC=α. (1)、如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是;(2)、如图2,当0°<α<180°时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)、拓展与应用:如图3,当α=120°时,点F为∠BAC平分线上的一点,且AB=AF,分别连接FB,FD,FE,FC,试判断△DEF的形状,并说明理由.
(1)、如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是;(2)、如图2,当0°<α<180°时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)、拓展与应用:如图3,当α=120°时,点F为∠BAC平分线上的一点,且AB=AF,分别连接FB,FD,FE,FC,试判断△DEF的形状,并说明理由.