辽宁省沈阳市育源集团2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列说法中，正确的是（）

A、 $\sqrt{9} = \pm 3$ B、带根号的数都是无理数 C、64的立方根是 $\pm 4$ D、 $- \sqrt{5}$ 是 $5$ 的一个平方根

查看试题解析
2. 已知点P（a+5，a﹣1）在第四象限，且到x轴的距离为2，则点P的坐标为（）

A、（4，﹣2） B、（﹣4，2） C、（﹣4，4） D、（2，﹣4）

查看试题解析
3. 如图，数轴上的A、B、C、D四点中，与数﹣ $\sqrt{3}$ 表示的点最接近的是（）

A、点A B、点B C、点C D、点D

查看试题解析
4. 以下列数据为三角形的三边长，能构成直角三角形的是（）

A、1， $\sqrt{3}$ ， 4 B、 $\frac{3}{5}$ ， $\frac{4}{5}$ ， 1 C、 $3^{2}$ ， $4^{2}$ ， $5^{2}$ D、6，7，8

查看试题解析
5. 有下列四个命题：①一次函数 $y = - 2 x + 4$ 的函数值随着x值的增大而增大；②等角的补角相等；③如果 $b ∥ a$ ， $c ∥ a$ ，那么 $b ∥ c$ ；④点 $M (- 2 ， 5)$ 关于x轴的对称点是N，则线段 $M N$ 的长是10，其中是真命题的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 直线 $y = a x + b$ （ $a \neq 0$ ）过点 $A (0 ， 1)$ ， $B (2 ， 0)$ ，则关于 $x$ 的方程 $a x + b = 0$ 的解为（）

A、 $x = 0$ B、 $x = 1$ C、 $x = 2$ D、 $x = 3$

查看试题解析
7. 下列说法正确的个数是（）
①函数 $y = - x + 2$ 的图象不经过第三象限
②一组数据5，6，7，6，8，10的众数和中位数都是6
③将 $y = - x - 3$ 的图象沿y轴向下平移3个单位长度后，图象经过原点
④式子 $\frac{\sqrt{a + 2}}{a + 3}$ 有意义的条件是 $a \geq - 2$ 且 $a \neq - 3$

A、1 B、2 C、3 D、4

查看试题解析
8. 小明在计算一组数据的方差时，列出的公式如下： $s^{2} = \frac{1}{n} \times [{(7 - \bar{x})}^{2} + {(8 - \bar{x})}^{2} + {(8 - \bar{x})}^{2} + {(8 - \bar{x})}^{2} + {(9 - \bar{x})}^{2}]$ ，根据公式信息，下列说法中，错误的是（）

A、数据个数是5 B、数据平均数是8 C、数据众数是8 D、数据方差是0

查看试题解析
9. 如图， $∠ B C D$ 是 $△ A B C$ 的一个外角，E是边AB上一点，下列结论错误的是（）

A、 $∠ B C D > ∠ A$ B、 $∠ B C D > ∠ 1$ C、 $∠ 2 > ∠ 3$ D、 $∠ B C D = ∠ A + ∠ B$

查看试题解析
10. 《孙子算经》记载：今有人盗库绢，不知所失几何？但闻草中分绢：人得六匹，盈六匹；人得七匹，不足七匹．问：人、绢各几何？意思是：如果每个人分6匹，还多出6匹，每个人分7匹，还差7匹，问：现在有多少人，有多少匹绢？设现在有x人，有绢y匹，下列所列方程（组）正确的是（）

A、 $6 x - 6 = 7 x + 7$ B、 $6 x + 6 = 7 x - 7$ C、 ${\begin{array}{l} y = 6 x + 6 \\ y - 7 = 7 x \end{array}$ D、 ${\begin{array}{l} y = 6 x - 6 \\ y + 7 = 7 x \end{array}$

查看试题解析

二、填空题

11. 计算 $(3 - \sqrt{5}) (3 + \sqrt{5})$ 的结果等于．

查看试题解析
12. 平面直角坐标系中，已知点 $A (5 ， - 8)$ ， $B (0 ， m)$ ，当线段AB有最小值时，m＝．

查看试题解析
13. 已知直线 $l_{1} ： y = - 3 x + b$ 与直线 $l_{2} ： y = - k x + m$ 在同一坐标系中的图象交于点 $(1 ， - 2)$ ，那么方程组 ${\begin{array}{l} 3 x + y = b \\ k x + y = m \end{array}$ 的解是．

查看试题解析
14. 一次函数 $y = x - b$ 的图象，沿着过点 $(1 ， 0)$ 且垂直于x轴的直线翻折后经过点 $(4 ， 2)$ ，则b的值为．

查看试题解析
15. 如图，在 $△ A B C$ 中，延长 $A B$ 至D，延长 $B C$ 至E，如果 $∠ 1 + ∠ 2 = 230 °$ ，则 $∠ A =$ ．

查看试题解析
16. 如图：在平面直角坐标系内有长方形 $O A B C$ ，点A，C分别在y轴，x轴上，点 $D (4 ， 3)$ 在 $A B$ 上，点E在 $O C$ 上，沿 $D E$ 折叠，使点B与点O重合，点C与点 $C_{1}$ 重合．若点P在坐标轴上，且 $△ A P C_{1}$ 面积是18，则点P坐标为．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(\sqrt{2} + \sqrt{3})}^{2} - \sqrt{24}$ ；

(2)、 $(\sqrt{\frac{1}{3}} + \sqrt{27}) \times \sqrt{3} - | \sqrt{5} - 2 |$ ．

查看试题解析
18. 解方程组： ${\begin{array}{l} 3 x + 2 y = 4 \\ 6 x - 2 y = - 1 \end{array}$ ．

查看试题解析
19. 如图， $△ A B C$ 的三个顶点都在方格纸的格点上，其中A点的坐标是 $(- 1 ， 0)$ ， B点的坐标是 $(- 3 ， 1)$ ， C点的坐标是 $(- 2 ， 3)$ ．

(1)、作 $△ A B C$ 关于y轴对称的图形 $△ D E F$ ，点A、B、C的对应点分别为D、E、F；则点 $E$ 的坐标为，点F的坐标为．

(2)、在（1）的条件下，点P为x轴正半轴上的动点，当 $△ P D E$ 为等腰三角形时，请直接写出点P的横坐标．

查看试题解析
20. “99公益日”是一年一度的全民公益活动日，学校组织学生参加慈善捐款活动，为了解学生捐款情况，随机调查了该校的部分学生，根据调查结果，绘制了如下的统计图1和图2．请根据相关信息，解答下列问题：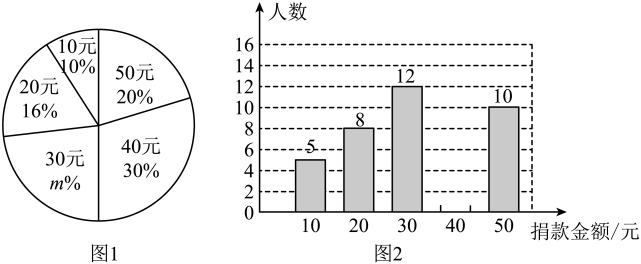

(1)、本次接受调查的学生人数为，图1中m的值为．

(2)、求统计的这组学生的捐款数据的平均数、众数和中位数．

(3)、根据统计的这组学生所捐款的情况，若该校共有1000名学生，估计该校共筹得善款多少元？

查看试题解析
21. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 的图象经过点 $A (- 2 ， 9)$ ，且与 $x$ 轴相交于点B，与y轴交于点D，与正比例函数 $y = 3 x$ 的图象相交于点C，点C的横坐标为1．

(1)、直接写出一次函数的函数解析式；

(2)、M为直线 $A B$ 上一点，过点M作y轴的平行线交 $y = 3 x$ 于点N，当 $M N = 2 O D$ 时，直接写出点M的坐标；

(3)、Q为直线 $A B$ 上一点，若 $S_{△ O C Q} = \frac{1}{2} S_{△ O B C}$ ， Q点坐标是．

查看试题解析
22. 毕业季即将到来，某礼品店准备购进一批适合学生的毕业纪念品．已知购进2件A礼品和6件B礼品共需180元，购进4件A礼品和3件B礼品共需135元．

(1)、设A，B两种礼品每件的进价分别是m元，n元，依题意可列方程组，解得m= ， n= ．

(2)、该店计划将2500元全部用于购进A，B这两种礼品，设购进A礼品x件，B礼品y件．
①则y关于x的关系式为；
②该店进货时，厂家要求A礼品的购进数量不少于60件．已知A礼品每件售价为20元，B礼品每件售价为35元．设该店全部售出这两种礼品可获利W元，则W关于x的关系式为，该店所获利润最大值为．

查看试题解析
23. 疫苗接种对新冠疫情防控至关重要.甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 $a$ 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务．乙地80天完成接种任务，甲、乙两地的接种人数 $y$ （万人）与接种所用时间 $x$ （天）之间的关系如图所示．

(1)、求乙地每天接种的人数万人；a的值为；

(2)、当甲地接种速度放缓后，求y关于x的函数解析式；并写出自变量x的取值范围；

(3)、当乙地完成接种任务时，甲地未接种疫苗的人数；

(4)、在 $0 < x \leq 80$ 这段时间内，当两地疫苗接种人数的差为3万人时，直接写出疫苗接种时间x的值．

查看试题解析
24. 如图， $∠ A O B = 40 °$ ， $O C$ 平分 $∠ A O B$ ，点D，E在射线 $O A$ ， $O C$ 上，点P是射线 $O B$ 上的一个动点，连接 $D P$ 交射线 $O C$ 于点F，设 $∠ O D P = x °$ ．

(1)、如图1，若 $D E$ $∥$ $O B$ ．
① $∠ D E O$ 的度数是 ▲ $°$ ，当 $D P ⊥ O E$ 时，x= ▲ ；
②若 $∠ E D F = ∠ E F D$ ，求x的值；

(2)、如图2，若 $D E ⊥ O A$ ，是否存在这样的x的值，使得 $∠ E F D = 4 ∠ E D F$ ？若存在，求出x的值；若不存在，说明理由．

查看试题解析
25. 【探索发现】如图1，等腰直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $C B = C A$ ，直线 $D E$ 经过点C，过A作 $A D ⊥ D E$ 于点D．过B作 $B E ⊥ D E$ 于点E，则 $△ B E C ≌ △ C D A$ ，我们称这种全等模型为“k型全等”．（不需要证明）

【迁移应用】已知：直线 $y = k x + 6 (k \neq 0)$ 的图象与x轴、y轴分别交于A、B两点．

(1)、如图2，当 $k = - \frac{3}{4}$ 时，在第一象限构造等腰直角 $△ A B E$ ， $∠ A B E = 90 °$ ；
①直接写出 $O A =$ ， $O B =$ ；
②点E的坐标；

(2)、如图3，当k的取值变化，点A随之在 $x$ 轴负半轴上运动时，在y轴左侧过点B作 $B N ⊥ A B$ ，并且 $B N = A B$ ，连接 $O N$ ，问 $△ O B N$ 的面积是否发生变化?（填“变”或“不变”），若不变，其值为；若变，请说明理由；

(3)、【拓展应用】如图4，当 $k = - \frac{3}{2}$ 时，直线 $l ： y = - 4$ 与y轴交于点D，点 $P (n ， - 4)$ 、Q分别是直线l和直线 $A B$ 上的动点，点C在x轴上的坐标为 $(10 ， 0)$ ，当 $△ P Q C$ 是以 $C Q$ 为斜边的等腰直角三角形时，点Q的坐标是．

查看试题解析