辽宁省大连市高新园区2022-2023学年八年级上学期期末考试数学试题
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列垃圾分类标识的图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各长度的木棒首尾相接可以组成三角形的是( )A、1,2,3 B、3,4,6 C、2,3,5 D、2,2,53. 某种冠状病毒的直径约为0.00000012米,用科学记数法可将0.00000012表示为( )A、 B、 C、 D、4. 已知 , 下列运算中正确的是( )A、 B、 C、 D、5. 如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,发现DE=AB.那么判定△ABC和△DEC全等的依据是( )
2. 下列各长度的木棒首尾相接可以组成三角形的是( )A、1,2,3 B、3,4,6 C、2,3,5 D、2,2,53. 某种冠状病毒的直径约为0.00000012米,用科学记数法可将0.00000012表示为( )A、 B、 C、 D、4. 已知 , 下列运算中正确的是( )A、 B、 C、 D、5. 如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,发现DE=AB.那么判定△ABC和△DEC全等的依据是( ) A、SSS B、SAS C、ASA D、AAS6. 已知 , , 则等于( )A、 B、 C、4 D、87. 一个多边形的内角和比外角和大180°,则这个多边形的边数是( )A、7 B、6 C、5 D、48. 如图,在四边形中, , 平分 , , 则的面积是( )
A、SSS B、SAS C、ASA D、AAS6. 已知 , , 则等于( )A、 B、 C、4 D、87. 一个多边形的内角和比外角和大180°,则这个多边形的边数是( )A、7 B、6 C、5 D、48. 如图,在四边形中, , 平分 , , 则的面积是( ) A、6 B、8 C、10 D、129. 如图,四边形是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式因式分解,其结果正确的是( )
A、6 B、8 C、10 D、129. 如图,四边形是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式因式分解,其结果正确的是( )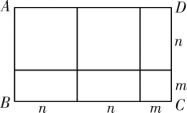 A、 B、 C、 D、10. 如图,在中,点D在边上, , , 则等于( )
A、 B、 C、 D、10. 如图,在中,点D在边上, , , 则等于( ) A、80° B、70° C、60° D、50°
A、80° B、70° C、60° D、50°二、填空题
-
11. 计算 .12. 如图,在中,的垂直平分线交边于点D,交边于点E,连接 . 若 , , 则的周长为 .
 13. 已知 , , m,n为正整数,则 .14. 甲、乙两个服装厂加工一批校服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套校服,甲厂比乙厂少用2天,设乙厂每天加工x套校服,则可列方程为 .15. 如图,在中, , , , 直线l是边的垂直平分线,点P是直线l上的一动点,则的最小值为 .
13. 已知 , , m,n为正整数,则 .14. 甲、乙两个服装厂加工一批校服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套校服,甲厂比乙厂少用2天,设乙厂每天加工x套校服,则可列方程为 .15. 如图,在中, , , , 直线l是边的垂直平分线,点P是直线l上的一动点,则的最小值为 .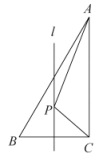 16. 如图,两个正方形的边长分别为a和b,若 , , 则阴影部分的面积为 .
16. 如图,两个正方形的边长分别为a和b,若 , , 则阴影部分的面积为 .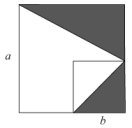
三、解答题
-
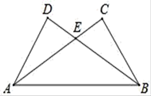
17. 解方程: .18. 计算 .19. 如图:AC⊥BC,BD⊥AD,BD与AC交于E,AD=BC,求证:BD=AC.
 20. 先化简,再求值: , 其中 .21. 如图,在中,是高.
20. 先化简,再求值: , 其中 .21. 如图,在中,是高. (1)、动手操作:利用尺规作图作的平分线,交边于点E(不写作法,保留作图痕).(2)、在(1)的条件下,若 , , 求的度数;22. 体育课上小明和小强进行1000米跑步测试,小强的跑步速度是小明的跑步速度a倍,两人同时起跑,小强比小明早t分钟跑完1000米.(1)、若 , , 求小明和小强的跑步速度;(2)、直接写出小强的跑步速度(用含a、t的代数式表示).23. 如图,是等边三角形,D是边上一点,在右侧作 , 且 , 连接 , .
(1)、动手操作:利用尺规作图作的平分线,交边于点E(不写作法,保留作图痕).(2)、在(1)的条件下,若 , , 求的度数;22. 体育课上小明和小强进行1000米跑步测试,小强的跑步速度是小明的跑步速度a倍,两人同时起跑,小强比小明早t分钟跑完1000米.(1)、若 , , 求小明和小强的跑步速度;(2)、直接写出小强的跑步速度(用含a、t的代数式表示).23. 如图,是等边三角形,D是边上一点,在右侧作 , 且 , 连接 , . (1)、求证:是等边三角形;(2)、若D是等边外一点,且与点A都在直线同侧,若 , 连接 , 画出图形,探究线段、、之间的数量关系,并说明理由.24. 阅读材料:利用完全平方公式可以将一些形如的多项式变形为的形式,我们把这样的变形方法叫做多项式的配方法,利用多项式的配方法及平方差公式能对一些多项式进行因式分解.
(1)、求证:是等边三角形;(2)、若D是等边外一点,且与点A都在直线同侧,若 , 连接 , 画出图形,探究线段、、之间的数量关系,并说明理由.24. 阅读材料:利用完全平方公式可以将一些形如的多项式变形为的形式,我们把这样的变形方法叫做多项式的配方法,利用多项式的配方法及平方差公式能对一些多项式进行因式分解.例如: .
根据以上材料,解答下列问题:
(1)、分解因式(利用配方法):;(2)、求多项式的最小值;(3)、比较与的大小,并说明理由.25. 综合与实践问题情境:数学活动课上,王老师出示了一个问题:如图,与都是等腰直角三角形,其中 , , , 且点D在延长线上,连接 . 求证 .
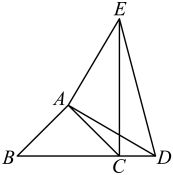 (1)、独立思考:请解答王老师提出的问题.(2)、实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.
(1)、独立思考:请解答王老师提出的问题.(2)、实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.“如图,连接 , 过A作交于F,探究线段与之间的数量关系,并证明.”
 (3)、问题解决:数学活动小组同学对上述问题进行特殊化研究,将绕点A旋转,使点E在延长线上,点D在延长线上,提出新的问题,请你解答.
(3)、问题解决:数学活动小组同学对上述问题进行特殊化研究,将绕点A旋转,使点E在延长线上,点D在延长线上,提出新的问题,请你解答.“如图,当点E在延长线上,点D在延长线上,连接 , 过B作且 , 连接交延长线于H,若 , 求的长.”
