北京市延庆区2022-2023学年八年级上学期期末数学试题
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列图形均为正多边形,恰有3条对称轴的图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 任意掷一枚骰子,下列情况出现的可能性最小的是( )A、面朝上的点数是偶数 B、面朝上的点数是奇数 C、面朝上的点数小于2 D、面朝上的点数大于23. 若在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、4. 下列各式中,最简二次根式是( )A、 B、 C、 D、5. 如图的两个三角形是全等三角形,其中角和边的大小如图所示,那么∠1的度数是( )
2. 任意掷一枚骰子,下列情况出现的可能性最小的是( )A、面朝上的点数是偶数 B、面朝上的点数是奇数 C、面朝上的点数小于2 D、面朝上的点数大于23. 若在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、4. 下列各式中,最简二次根式是( )A、 B、 C、 D、5. 如图的两个三角形是全等三角形,其中角和边的大小如图所示,那么∠1的度数是( ) A、 B、 C、 D、6. 下列运算中,正确的是( )A、 B、 C、 D、7. 下列变形正确的是( )A、 B、 C、 D、8. 如果n为整数,且 , 那么n的值为( )A、2 B、3 C、4 D、59. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、 B、 C、 D、6. 下列运算中,正确的是( )A、 B、 C、 D、7. 下列变形正确的是( )A、 B、 C、 D、8. 如果n为整数,且 , 那么n的值为( )A、2 B、3 C、4 D、59. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )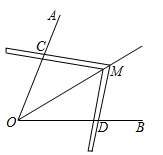 A、 B、 C、 D、10. 如图,中, , 是的平分线,E是上一点,连接 . 若 , , 则的长是( )
A、 B、 C、 D、10. 如图,中, , 是的平分线,E是上一点,连接 . 若 , , 则的长是( ) A、 B、4 C、 D、2
A、 B、4 C、 D、2二、填空题
-
11. 若分式的值为0,则x的值为 .12. 如图,将一副直角三角板,按如图所示的方式摆放,则∠α的度数是 .
 13. 请写出一个小于4的无理数:14. 计算: .15. 如图,和中, , 在不添加任何辅助线的情况下,请你添加一个条件 , 使得和全等,(写出一个即可)
13. 请写出一个小于4的无理数:14. 计算: .15. 如图,和中, , 在不添加任何辅助线的情况下,请你添加一个条件 , 使得和全等,(写出一个即可) 16. 等腰三角形有两条边长分别为和 , 则这个等腰三角形的周长为cm.17. 如图,在中, , 是的角平分线,如果 , , 那么 .
16. 等腰三角形有两条边长分别为和 , 则这个等腰三角形的周长为cm.17. 如图,在中, , 是的角平分线,如果 , , 那么 . 18. 阅读下面材料:
18. 阅读下面材料:已知: , 依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,为半径画弧;
步骤2:以B为圆心,为半径画弧,两弧交于点D;
步骤3:连接 , 交延长线于点E.

下列叙述正确的是 . (填写序号)
①垂直平分线段;②平分;③;④ .
三、解答题
-
19. 计算:20. 计算:(1)、(2)、如果 , 求代数式的值.21. 解方程:(1)、(2)、22. 如图, , 且是的平分线.
求证: .
 23. 列方程解应用题:某生产线用机器人搬运产品.A型机器人比B型机器人每小时多搬运20件,A型机器人搬运600件产品所用的时间与B型机器人搬运400件产品所用的时间相等.问B型机器人每小时搬运多少件产品?24. 如图,点A,B,C,D在一条直线上, , , . 请判断与的关系,并证明你的结论.
23. 列方程解应用题:某生产线用机器人搬运产品.A型机器人比B型机器人每小时多搬运20件,A型机器人搬运600件产品所用的时间与B型机器人搬运400件产品所用的时间相等.问B型机器人每小时搬运多少件产品?24. 如图,点A,B,C,D在一条直线上, , , . 请判断与的关系,并证明你的结论. 25. 老师留的作业中有这样一道计算题: , 小明完成的过程如下:
25. 老师留的作业中有这样一道计算题: , 小明完成的过程如下:(第一步)
(第二步)
(第三步)
老师发现小明的解答过程有错误.
(1)、请你帮助小明分析错误原因.小明的解答从第步开始出现错误,错误的原因是;正确的解题思路是 .
(2)、请写出正确解答过程.26. 《九章算术》卷九“勾股”中记载:“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺;牵着绳索(绳索与地面接触)退行,在距木柱根部8尺处时绳索用尽.问绳索长多少?即:如图,在中, , , , 求的长. 27. 在中, , , , 点D为边上的一个动点,连接 , 点A关于直线的对称点为点E,直线交于点F.
27. 在中, , , , 点D为边上的一个动点,连接 , 点A关于直线的对称点为点E,直线交于点F. (1)、如图1,当时,根据题意将图形补充完整,并直接写出的度数;(2)、如图2,当时,用等式表示线段之间的数量关系,并证明.28. 在同一平面内的两个图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M,N间的“最距离”,记作: .
(1)、如图1,当时,根据题意将图形补充完整,并直接写出的度数;(2)、如图2,当时,用等式表示线段之间的数量关系,并证明.28. 在同一平面内的两个图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M,N间的“最距离”,记作: .如图,点B,C在数轴上表示的数分别为0,2,于点B,且 .
 (1)、若点D在数轴上表示的数为5,求d(点D,);(2)、若点E,F在数轴上表示的数分别是x, , 当d(线段 , )时,求x的取值范围.
(1)、若点D在数轴上表示的数为5,求d(点D,);(2)、若点E,F在数轴上表示的数分别是x, , 当d(线段 , )时,求x的取值范围.