北京市西城区2022-2023学年八年级上学期期末数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 以下是用电脑字体库中的一种篆体写出的“诚信友善”四字,若把它们抽象为几何图形,从整体观察(个别细微之处的细节可以忽略不计),其中大致是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 地处北京怀柔科学城的“北京光源”()是我国第一台高能同步辐射光源,在施工时严格执行“防微振动控制”的要求,控制精度级别达到纳米(nm)级.1nmm.将用科学记数法表示应为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 下列长度的三条线段能组成三角形的是( )A、5,5,5 B、5,5,10 C、5,6,12 D、3,4,75. 如图, , , . 有下列结论:
2. 地处北京怀柔科学城的“北京光源”()是我国第一台高能同步辐射光源,在施工时严格执行“防微振动控制”的要求,控制精度级别达到纳米(nm)级.1nmm.将用科学记数法表示应为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 下列长度的三条线段能组成三角形的是( )A、5,5,5 B、5,5,10 C、5,6,12 D、3,4,75. 如图, , , . 有下列结论: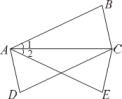
①把沿直线翻折180°,可得到;
②把沿线段的垂直平分线翻折180°,可得到;
③把沿射线DC方向平移与相等的长度,可得到 .
其中所有符合题意结论的序号是( )
A、①② B、①③ C、②③ D、①②③6. 下列各式从左到右的变形正确的是( )A、 B、 C、 D、7. 图1所示的是一把木工台锯时使用的六角尺,它能提供常用的几种测量角度.在图2的六角尺示意图中,x的值为( ) A、 B、 C、 D、8. 如图,在中, , 的度数为α.点P在边上(点P不与点B,点C重合),作于点D,连接 , 取上一点E,使得 , 连接 , 并延长交于点F之后,有 . 若记的度数为x,则下列关于的表达式正确的是( )
A、 B、 C、 D、8. 如图,在中, , 的度数为α.点P在边上(点P不与点B,点C重合),作于点D,连接 , 取上一点E,使得 , 连接 , 并延长交于点F之后,有 . 若记的度数为x,则下列关于的表达式正确的是( )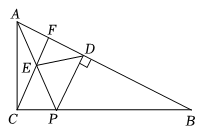 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算:(1)、=;(2)、 .10. 若分式有意义,则字母x满足的条件是 .11. 分解因式: .12. 在平面直角坐标系中,关于x轴对称的点的坐标为 .13. 小王读到关于京唐城际铁路的新闻报道后,搜集该线路的相关信息制作了下表,表中两个区间段(线路的一部分)运行时相应所用的时间比约少 , 那么可列出关于v的方程为 .
区间段
区间近似里程
区间设计最高时速
相应所用时间
北京城市副中心站−香河站
47.8
t1
香河站−唐山西站
87
v
t2
14. 三个长方形纸片如图1所示无缝隙地拼接在一起,它们的边长分别标记在图1中.现将拼接后的纸片用图2所示方式重新分割成三个长方形A,B,C.根据图2与图1的关系写出一个等式:(用含a,b,c,d,e,f的式子表示). 15. 如图,在中, , 于点D,于点C, . 点E,点F分别在线段上, , 连接 .
15. 如图,在中, , 于点D,于点C, . 点E,点F分别在线段上, , 连接 . (1)、图中与相等的线段是;(2)、当取最小值时°
(1)、图中与相等的线段是;(2)、当取最小值时°三、解答题
-
16. 如图,在四边形中, , 平分 , .
 (1)、画出的高;(2)、的面积等于 .17. 计算:(1)、;(2)、;(3)、18. 已知 , 求代数式的值.19. 解方程:20. 如图,A,D两点在所在直线同侧, , 垂足分别为A,D.的交点为E, . 求证: .
(1)、画出的高;(2)、的面积等于 .17. 计算:(1)、;(2)、;(3)、18. 已知 , 求代数式的值.19. 解方程:20. 如图,A,D两点在所在直线同侧, , 垂足分别为A,D.的交点为E, . 求证: . 21. 如图,在平面直角坐标系中, , , , . 点B与点C关于直线l对称,直线l与的交点分别为点D,E.
21. 如图,在平面直角坐标系中, , , , . 点B与点C关于直线l对称,直线l与的交点分别为点D,E. (1)、求点A到的距离;(2)、连接 , 补全图形并求的面积;(3)、若位于x轴上方的点P在直线l上, , 直接写出点P的坐标.22.(1)、设计作平行线的尺规作图方案:已知:直线及直线外一点P.求作:经过点P的直线 , 使得 .
(1)、求点A到的距离;(2)、连接 , 补全图形并求的面积;(3)、若位于x轴上方的点P在直线l上, , 直接写出点P的坐标.22.(1)、设计作平行线的尺规作图方案:已知:直线及直线外一点P.求作:经过点P的直线 , 使得 .
分析:如图1所示,之前我们学过“推”三角尺画平行线,这种画法的实物操作图可以启发我们预设目标示意图,分析尺规作图思路.

①请参考以上内容完成尺规作图,保留作图痕迹,不必写作法;
②在①中用到的判定的依据是 .
(2)、已知:如图,在中, , .求作:凸四边形 , 使得 , 且为等腰三角形.

请完成尺规作图并写出所求作的四边形,保留作图痕迹,不必写作法.
23. 在中, , 在上截取 , 连接 . 在的外部作 , 且交的延长线于点E.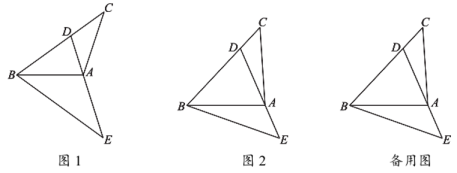 (1)、作图与探究:
(1)、作图与探究:①小明画出图1并猜想 . 同学小亮说“要让你这个结论成立,需要增加条件: ▲ °.”
请写出小亮所说的条件;
②小明重新画出图2并猜想 . 他证明的简要过程如下:

请你判断小明的证明是否正确并说明理由;
(2)、证明与拓展:①借助小明画出的图2证明;
②延长到F,使 , 连结 . 补全图形,猜想与的数量关系并加以证明.
24. 在单位长度为1的正方形网格中,如果一个凸多边形的顶点都是网格线交点,我们称其为格点凸多边形,并记该格点多边形的面积为S,多边形内部的格点数为N,多边形边上的格点数为L.(1)、对于图中的五个凸多边形,补全以下表格: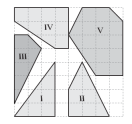
多边形
面积S
内部格点数N
边上格点数L
Ⅰ
Ⅱ
7
4
8
8
Ⅲ
Ⅳ
9
5
10
10
Ⅴ
11
11
(2)、借助以上表格猜想格点凸多边形的面积公式:S与的数量关系可用等式表示为;(3)、已知格点长方形ABCD,设其边长 , 其中m,n为正整数.请以格点长方形为例,尝试证明(2)中的格点凸多边形的面积公式.25. 阅读两位同学的探究交流活动过程:a.小明在做分式运算时发现如下一个等式,并对它进行了证明.
①
b.小明尝试写出了符合这个特征的其他几个等式:
②
③
④
c.小明邀请同学小亮根据上述规律写出第⑤个等式和第n个等式(用含n的式子表示,n为正整数);
d.小亮对第n个等式进行了证明.
解答下列问题:
(1)、第⑤个等式是;(2)、第n个等式是;(3)、请你证明第n个等式成立.26. 在平面直角坐标系中,对于点P,点M给出如下定义:如果点P与原点O的距离为a,点M与点P的距离是a的k倍(k为整数),那么称点M为点P的“k倍关联点”.(1)、当时,①如果点的2倍关联点M在x轴上,那么点M的坐标为;
②如果点是点的k倍关联点,且满足 , , 那么整数k的最大值为;
(2)、已知在中, , , , . 若 , 且在的边上存在点的2倍关联点Q,求b的取值范围.