北京市顺义区2022-2023学年八年级上学期数学期末试卷

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、2 B、 $\pm 2$ C、 $\sqrt{2}$ D、16

查看试题解析
2. 利用直角三角板，作 $△ A B C$ 的高线，下列作法正确的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各数中，无理数是（）

A、0 B、 $\sqrt[3]{2}$ C、 $\frac{1}{3}$ D、 $\sqrt{9}$

查看试题解析
4. 下列事件中，属于随机事件的是（）

A、太阳从西边升起来了 B、张叔叔申请了北京市小客车购买指标，在申请后的第一次“摇号”时就中签 C、任意投掷一枚骰子，面朝上的点数是7 D、用长度分别是 $2 c m$ ， $4 c m$ ， $5 c m$ 的三条线段首尾顺次相接可组成一个三角形

查看试题解析
5. 甲骨文是中国的一种古代文字，是汉字的早期形式，有时候也被认为是汉字的书体之一，也是现存中国王朝时期最古老的一种成熟文字．下图为甲骨文对照表中的四个字，若把这四个甲骨文的文字抽象为几何图形，其中最接近轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 如果把分式 $\frac{2 m}{m - n}$ 中的m，n都扩大为原来的2倍，那么分式的值（）

A、扩大为原来的2倍 B、缩小为原来的 $\frac{1}{2}$ C、扩大为原来的4倍 D、不变

查看试题解析
7. 解方程 $\frac{3}{x - 1} = 1 - \frac{x}{x + 1}$ ，去分母后正确的是（）

A、 $3 (x + 1) = 1 - x (x - 1)$ B、 $3 (x + 1) = (x + 1) (x - 1) - x (x - 1)$ C、 $3 (x + 1) = (x + 1) (x - 1) - x (x + 1)$ D、 $3 (x - 1) = 1 - x (x + 1)$

查看试题解析
8. 如图，每个小方格的边长为1，A ， B两点都在小方格的顶点上，点C也是图中小方格的顶点，并且△ABC是等腰三角形，那么点C的个数为（）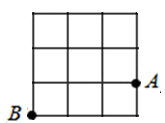

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 若分式 $\frac{x + 1}{x}$ 值为0，则 $x$ 的值为.

查看试题解析
10. 已知 $\sqrt{x - 3}$ 是二次根式，则x的取值范围是．

查看试题解析
11. 计算： ${(- \frac{a}{2 b})}^{2} \div (- \frac{a^{2}}{3 b}) =$ .

查看试题解析
12. 如图， $A C$ 与 $B D$ 相交于点O， $O A = O C$ ，那么要得到 $△ A O D ≌ △ C O B$ ，可以添加一个条件是（填一个即可）.

查看试题解析
13. 居家上网课期间，小燕在学习之余与妈妈要玩一次转盘游戏，选项与所占比例如图所示，则她不看电视的可能性为．

查看试题解析
14. 如图是某路口处草坪的一角，当行走路线是 $A \to C \to B$ 时，有人为了抄近道而避开路的拐角 $∠ A C B$ $(∠ A C B = 90 °)$ ，于是在草坪内走出了一条不该有的捷径路 $A B$ .某学习实践小组通过测量可知， $A C$ 的长约为6米， $B C$ 的长约为8米，为了提醒居民爱护草坪，他们想在A， $B$ 处设立“踏破青白可惜，多行数步无妨”的提示牌．则提示牌上的“多行数步”是指多行米．

查看试题解析
15. 对于两个非零的实数a，b，定义新运算 $a ※ b = \frac{1}{b} - \frac{1}{a}$ ．例如： $4 ※ 3 = \frac{1}{3} - \frac{1}{4} = \frac{1}{12}$ ．则 $2 ※ (- 2) =$ ；若 $2 ※ (2 x - 1) = 1$ ，则x的值为．

查看试题解析
16. 如图， $O A = 2 \sqrt{2}$ ， $∠ A O P = 45 °$ ，点B在射线 $O P$ 上，若 $△ A O B$ 为钝角三角形，则线段 $O B$ 长的取值范围是.

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{2}{3 x^{2}} \cdot \frac{x^{3}}{6}$ ；

(2)、 $\frac{1}{3 a} - \frac{1}{6 b}$ .

查看试题解析
18. 计算：

(1)、 $\sqrt{8} + \sqrt{2}$ ；

(2)、 $\sqrt{12} \div \sqrt{6}$ ．

查看试题解析
19. 计算： $(\frac{a + 1}{a - 1} + \frac{1 - a}{a + 1}) \cdot \frac{a + 1}{a}$ ．

查看试题解析
20. 计算： $\sqrt[3]{27} + | - \sqrt{3} | - \frac{3}{\sqrt{3}}$ ．

查看试题解析
21. 计算： ${(\sqrt{6} - \sqrt{3})}^{2} - \sqrt{2} (\sqrt{8} - \sqrt{\frac{1}{2}})$ ．

查看试题解析
22. 已知：如图，AB＝DE，AC＝DF，BE＝CF．求证：∠A＝∠D．

查看试题解析
23. 先化简，再求值： $\frac{1}{x - 1} \div \frac{x + 2}{x^{2} - x} - \frac{x - 1}{x + 2}$ ，其中 $x = \sqrt{2} - 2$ ．

查看试题解析
24. 下面是晓东设计的“经过已知直线外一点作这条直线的垂线”的尺规作图过程．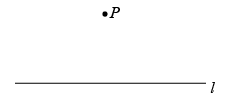
已知：直线l及直线l外一点P．
求作：直线l的垂线，使其经过点P．
作法：如图，
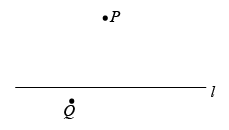
①任取一点Q，使点Q与点P在直线l两侧；
②以P为圆心， $P Q$ 长为半径作弧交直线l于A，B两点；
③分别以A，B为圆心， $A P$ 长为半径作弧，两弧在直线l下方交于点C；
④作直线 $P C$ ．
所以直线 $P C$ 为所求作的垂线．
根据晓东设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；（保留作图痕迹）

(2)、完成下面的证明．
证明：连接 $P A$ ， $P B$ ， $A C$ ， $B C$ ，
∵ $P A = P B$ ，
∴点P在线段 $A B$ 的垂直平分线上（）（填推理的依据）．
∵_▲_ ，
∴点C在线段 $A B$ 的垂直平分线上．
∴直线 $P C$ 为线段 $A B$ 的垂直平分线．
即 $P C ⊥ l$ ．

查看试题解析
25. 如图所示，有两个质地均匀且可以转动的转盘，转盘一被分成6个全等的扇形区域，转盘二被分成8个全等的扇形区域．在转盘的适当地方涂上灰色，末涂色部分为白色．用力转动转盘，请你通过计算判断，当转盘停止后哪一个转盘指针指向灰色的可能性大．

查看试题解析
26. 一些数按某种规律排列如下：
第一行
1
$\sqrt{2}$
第二行
$\sqrt{3}$
2
$\sqrt{5}$
$\sqrt{6}$
第三行
$\sqrt{7}$
$2 \sqrt{2}$
3
$\sqrt{10}$
$\sqrt{11}$
$2 \sqrt{3}$
第四行
$\sqrt{13}$
$\sqrt{14}$
$\sqrt{15}$
4
$\sqrt{17}$
$3 \sqrt{2}$
$\sqrt{19}$
$2 \sqrt{5}$
……

(1)、根据排列的规律，写出第5行从左数第4个数；

(2)、写出第n（n是正整数）行，从左数第 $n + 1$ 个数（用含n的代数式表示）．

查看试题解析
27. 数学课上，同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法．
小惠说：如图，我用两把完全相同的直尺可以作出角的平分线．画法如下：
①第一把直尺按图1所示放置，使一条边和射线 $O B$ 对齐；
②第二把直尺按图2所示放置，使一条边和射线 $O A$ 对齐；
如图3，两把直尺的另一条边相交于点P，作射线 $O P$ ．射线 $O P$ 是 $∠ A O B$ 的平分线．
小旭说：我用两个直角三角板可以画角的平分线．
小宇说：只用一把刻度尺就可以画角的平分线．
……
请你也参与探讨，解决以下问题：

(1)、小惠的做法符合题意吗？如果正确，请说明依据，如果错误，请说明理由；

(2)、请你参考小旭或小宇的思路，或根据自己的思路，画出下图中 $∠ C D E$ 的平分线，并简述画图的过程．

查看试题解析
28. 某中学为配合开展“垃圾分类进校园”活动，新购买了一批不同型号的垃圾桶，学校先用2400元购买了一批给班级使用的小号垃圾桶，再用3200元购买了一批放在户外使用的大号垃圾桶，已知一个大号垃圾桶的价格是小号垃圾桶的4倍．且大号垃圾桶购买的数量比小号垃圾桶少50个，求一个小号垃圾桶的价格．

查看试题解析
29. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D，过点D作 $D E ∥ A B$ 交 $B C$ 于点E， $D F ⊥ A B$ ，垂足为点F．

(1)、求证： $B E = D E$ ；

(2)、若 $D E = 2$ ， $D F = \sqrt{3}$ ，求 $B D$ 的长．

查看试题解析
30. 如图， $△ A B C$ 为等边三角形，在 $∠ B A C$ 内作射线 $A P$ $(∠ B A P < 30 °)$ ，点B关于射线 $A P$ 的对称点为点D，连接 $A D$ ，作射线 $C D$ 交 $A P$ 于点E，连接 $B E$ ．

(1)、依题意补全图形；

(2)、设 $∠ B A P = α$ ，求 $∠ B C E$ 的大小（用含 $α$ 的代数式表示）；

(3)、用等式表示 $E A$ ， $E B$ ， $E C$ 之间的数量关系，并证明．

查看试题解析

第一行				1	$\sqrt{2}$
第二行			$\sqrt{3}$	2	$\sqrt{5}$	$\sqrt{6}$
第三行		$\sqrt{7}$	$2 \sqrt{2}$	3	$\sqrt{10}$	$\sqrt{11}$	$2 \sqrt{3}$
第四行	$\sqrt{13}$	$\sqrt{14}$	$\sqrt{15}$	4	$\sqrt{17}$	$3 \sqrt{2}$	$\sqrt{19}$	$2 \sqrt{5}$
……