安徽省合肥市蜀山区2022-2023学年八年级上学期数学上学期期末质量检测卷

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{1}{5}}$ C、 $\sqrt{3}$ D、 $\sqrt{1.5}$

查看试题解析
2. 下列长度的三条线段，首尾顺次相连能组成三角形的是（）

A、 $2 ， 3 ， 6$ B、 $4 ， 4 ， 8$ C、 $5 ， 9 ， 14$ D、 $6 ， 12 ， 13$

查看试题解析
3. 新能源、绿色能源将成为产业发展的新趋势，下列新能源环保图标中，图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列事件中的随机事件是（）

A、在数轴上任取一个点，它表示的数是实数 B、任意画一个三角形，恰好同一边上的高线与中线重合 C、任意画一个三角形，其内角和是180° D、用长度分别是3，3，6的木条首尾顺次相连可组成一个等腰三角形

查看试题解析
5. 如果 $a + b = 2$ ，那么代数式 $(a - \frac{b^{2}}{a}) \cdot \frac{a}{a - b}$ 的值是（）

A、2 B、 $- 2$ C、1 D、 $- 1$

查看试题解析
6. 图1是一路灯的实物图，图2是该路灯的平面示意图， $∠ M A C = 50 °$ ， $∠ A C B = 20 °$ ，则图2中 $∠ C B A$ 的度数为（）

A、 $15 °$ B、 $20 °$ C、 $30 °$ D、 $50 °$

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ，以点A为圆心，适当长为半径画弧，分别交 $A B$ 、 $A C$ 于点D，E，再分别以点D、E为圆心，大于 $\frac{1}{2} D E$ 为半径画弧，两弧交于点F，作射线 $A F$ 交边 $B C$ 于点G，若 $B G = 1$ ， $A C = 4$ ，则 $△ A C G$ 的面积是（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，已知 $△ A B C$ $(A C < B C)$ ，用尺规在 $B C$ 边上确定一点P，使 $P A + P C = B C$ ．下面四种作图中，正确的是（）

A、以B为圆心， $B A$ 为半径画弧，交 $B C$ 于点P，点P为所求 B、以C为圆心， $C A$ 为半径画弧，交 $B C$ 于点P，点P为所求 C、作 $A C$ 的垂直平分线交 $B C$ 于点P，点P为所求 D、作 $A B$ 的垂直平分线交 $B C$ 于点P，点P为所求

查看试题解析

二、填空题

9. 若代数式 $\frac{1}{x - 1}$ 有意义，则实数x的取值范围是.

查看试题解析
10. 比较大小：7 $5 \sqrt{2}$ （填“ $>$ ”，“ $<$ ”或“ $=$ ”）

查看试题解析
11. 六张卡片的正面分别写有 $π$ ， $\frac{1}{3}$ ， $\sqrt{5}$ ， 0， $\sqrt[3]{8}$ ， $- 0.1212212221$ 这六个数，将卡片的正面朝下（反面完全相同）放在桌子上，从中任意抽取一张，卡片上的数字为无理数的可能性大小是．

查看试题解析
12. 在测量一个小口圆形容器的壁厚时，小明用“x型转动钳”按如图方法进行测量，其中 $O A = O D$ ， $O B = O C$ ，测量 $A B$ 的长度即可知道 $C D$ 的长度，理由是根据可证明 $△ A O B ≌ △ D O C$ ．

查看试题解析
13. 如图所示的正方形网格中，每一个小正方形的面积均为1，正方形 $A B C M$ ， $C D E N$ ， $M N P Q$ 的顶点都在格点上，则正方形 $M N P Q$ 的面积为．

查看试题解析
14. 若 $\sqrt{x + y} + {(y - 2)}^{2} = 0$ ，则 $x y$ 的值为．

查看试题解析
15. 如图所示的网格是正方形网格，则 $∠ A B C + ∠ B A C =$ °（点A，B，C是网格线交点）．

查看试题解析
16. 如图， $∠ B = 45 °$ ， $B C = 3 \sqrt{2}$ ，点A在射线 $B M$ 上，连接 $A C$ ，

(1)、若 $A C ⊥ B M$ ，则 $A C =$ ．

(2)、设 $A C = d$ ，若 $△ A B C$ 的形状、大小是唯一确定的，则d的取值范围是．

查看试题解析

三、解答题

17. 计算： ${(\sqrt{2})}^{2} - \sqrt{27} + {(\frac{1}{2})}^{- 2} + | 1 - \sqrt{3} |$ ．

查看试题解析
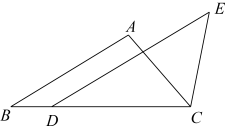
18. 计算 $(\sqrt{8} + \sqrt{3}) \times \sqrt{6} - 4 \sqrt{\frac{1}{2}}$

查看试题解析
19. 如图，在△ABC中，点D在边BC上，CD=AB，DE∥AB，∠DCE=∠A.求证：DE=BC.

查看试题解析
20. 化简： $(\frac{1}{a - 2} - \frac{3}{a^{2} - 4}) \div \frac{a - 1}{a^{2} + 2 a}$

查看试题解析
21. 解方程： $\frac{x + 1}{x - 1} - \frac{6}{x^{2} - 1} = 1$

查看试题解析
22. 如图是 $4 \times 4$ 正方形网格，其中有两个小正方形是涂黑的，请再选择三个小正方形并涂黑，使整个涂成黑色的图形成为轴对称图形．请补全图形，并且画出对称轴（如图例），要求所画的四种方案不能重复．

查看试题解析
23. 下面是“已知斜边作一个直角三角形”的尺规作图过程．
已知：线段 $A B$
求作：一个直角三角形 $A B C$ ，使线段 $A B$ 为斜边．
作法：①过A任意作一条射线l；
②在射线l上任取两点D，E；
③分别以点D，E为圆心， $D B$ ， $E B$ 长为半径作弧，两弧相交于点P；
④作射线 $B P$ 交射线l于点C．
则 $△ A B C$ 就是所求作的直角三角形．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、证明：连接 $D P$ ， $E P$
∵ $D B =$ _▲_
∴点D在线段 $B P$ 的垂直平分线上（）．（填推理的依据）
同理可证：点E在线段 $B P$ 的垂直平分线上
根据两点确定一条直线，可知 $D E$ 是线段 $B P$ 的垂直平分线．
∴ $∠ A C B = 90 °$ ．

(3)、在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，如果 $∠ A = 30 °$ ，猜想： $B C$ 与 $A B$ 满足的数量关系，并证明．

查看试题解析
24. 2022年我国已成为全球最大的电动汽车市场，电动汽车在保障能源安全，改善空气质量等方面较传统汽车都有明显优势，经过对某款电动汽车和某款燃油车的对比调查发现，电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元．若充电费和加油费均为200元时，电动汽车可行驶的总路程是燃油车的4倍，求这款电动汽车平均每公里的充电费．

查看试题解析
25. 阅读下列材料，然后回答问题．
已知 $a > 0$ ， $S_{1} = \frac{1}{a}$ ， $S_{2} = - S_{1} - 1$ ， $S_{3} = \frac{1}{S_{2}}$ ， $S_{4} = - S_{3} - 1$ ， $S_{5} = \frac{1}{S_{4}}$ ， …．
当n为大于1的奇数时， $S_{n} = \frac{1}{S_{n - 1}}$ ；当n为大于1的偶数时， $S_{n} = - S_{n - 1} - 1$ ．

(1)、求 $S_{3}$ ；（用含a的代数式表示）

(2)、直接写出 $S_{2023} =$ ；（用含a的代数式表示）

(3)、计算： $S_{1} + S_{2} + S_{3} + \cdot \cdot \cdot + S_{2022}$

查看试题解析
26. 如图 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， D是 $A C$ 边上一点，连接 $B D$ ， $E C ⊥ A C$ 垂足为点C，且 $A E = B D$ ， $A E$ 交线段 $B C$ 于点F．

(1)、在图1中画出正确的图形，并证明 $C E = A D$ ；

(2)、当 $∠ C F E = ∠ A D B$ 时，求证： $B D$ 平分 $∠ A B C$ ．

查看试题解析
27. 已知：线段 $A B$ 及过点A的直线l．如果线段 $A C$ 与线段 $A B$ 关于直线l对称，连接 $B C$ 交直线l于点D，以 $A C$ 为边作等边 $△ A C E$ ，使得点E在 $A C$ 的下方，作射线 $B E$ 交直线l于点F，连结 $C F$ ．

(1)、根据题意补全图形；

(2)、如果 $∠ B A D = α$ $(30 ° < α < 60 °)$
① $∠ A B E =$ ▲ ；（用含有 $α$ 代数式表示）
②用等式表示线段 $F A$ ， $F E$ 与 $F C$ 的数量关系，并证明．

查看试题解析