天津市河北区2022-2023学年九年级上学期期末线上质量检测数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、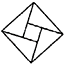 2. 在平面直角坐标系中,若点与点关于原点对称,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列事件中,是必然事件的是( )A、投掷一枚硬币,向上一面是反面 B、同旁内角互补 C、打开电视,正播放电影《守岛人》 D、任意画一个三角形,其内角和是4. 若m、n是一元二次方程x2+3x﹣9=0的两个根,则 的值是( )A、4 B、5 C、6 D、125. 方程的根是( )A、 , B、 , C、 , D、 ,6. 如图,将绕点逆时针旋转,得到 , 若点A的对应点恰好在线段上,且平分 , 记线段与线段的交点为 . 下列结论中,错误的是( )
2. 在平面直角坐标系中,若点与点关于原点对称,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列事件中,是必然事件的是( )A、投掷一枚硬币,向上一面是反面 B、同旁内角互补 C、打开电视,正播放电影《守岛人》 D、任意画一个三角形,其内角和是4. 若m、n是一元二次方程x2+3x﹣9=0的两个根,则 的值是( )A、4 B、5 C、6 D、125. 方程的根是( )A、 , B、 , C、 , D、 ,6. 如图,将绕点逆时针旋转,得到 , 若点A的对应点恰好在线段上,且平分 , 记线段与线段的交点为 . 下列结论中,错误的是( )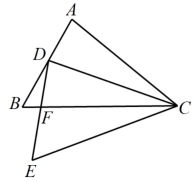 A、 B、 C、 D、7. 一元二次方程的解是( )A、 B、 C、 D、8. 关于二次函数 ,下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数有最大值,是大值是5 D、当 时,y随x的增大而增大9. 将抛物线先向右平移3个单位长度,再向上平移2个单位长度,平移后抛物线的顶点坐标是( )A、 B、 C、 D、10. 关于反比例函数 ,下列说法中错误的是( )A、点在它的图象上 B、图象关于直线对称 C、当时,随的增大而增大 D、它的图象位于第一.三象限11. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A、 B、 C、 D、7. 一元二次方程的解是( )A、 B、 C、 D、8. 关于二次函数 ,下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数有最大值,是大值是5 D、当 时,y随x的增大而增大9. 将抛物线先向右平移3个单位长度,再向上平移2个单位长度,平移后抛物线的顶点坐标是( )A、 B、 C、 D、10. 关于反比例函数 ,下列说法中错误的是( )A、点在它的图象上 B、图象关于直线对称 C、当时,随的增大而增大 D、它的图象位于第一.三象限11. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( ) A、
A、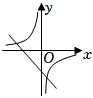 B、
B、 C、
C、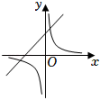 D、
D、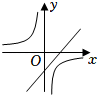 12. 如图,AB是的弦,半径于点D, , 点P在圆周上,则等于( )
12. 如图,AB是的弦,半径于点D, , 点P在圆周上,则等于( )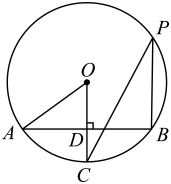 A、27° B、30° C、32° D、36°13. 如图,正六边形 内接于 ,正六边形的周长是12,则 的半径是( )
A、27° B、30° C、32° D、36°13. 如图,正六边形 内接于 ,正六边形的周长是12,则 的半径是( )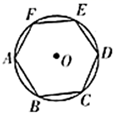 A、3 B、2 C、 D、14. 如图,为的直径,与相切于点 , 交的延长线于点 , 且 . 若 , 则半径长为( )
A、3 B、2 C、 D、14. 如图,为的直径,与相切于点 , 交的延长线于点 , 且 . 若 , 则半径长为( )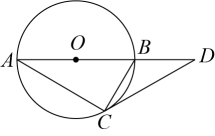 A、2 B、3 C、 D、15. 已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为 , 则该圆锥的底面半径是( )A、1 B、 C、2 D、16. 在一个不透明袋子中装有3个红球,2个白球,它们除颜色外其余均相同,随机从中摸出一球,记录下颜色后将它放回,充分摇匀后,再随机摸出一球,则两次都摸到红球的概率是( ).A、 B、 C、 D、17. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
A、2 B、3 C、 D、15. 已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为 , 则该圆锥的底面半径是( )A、1 B、 C、2 D、16. 在一个不透明袋子中装有3个红球,2个白球,它们除颜色外其余均相同,随机从中摸出一球,记录下颜色后将它放回,充分摇匀后,再随机摸出一球,则两次都摸到红球的概率是( ).A、 B、 C、 D、17. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( ) A、5 B、6 C、 D、18. 如图,两个反比例函数y1=和y2=在第一象限内的图象分别是C1和C2 , 设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A、5 B、6 C、 D、18. 如图,两个反比例函数y1=和y2=在第一象限内的图象分别是C1和C2 , 设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )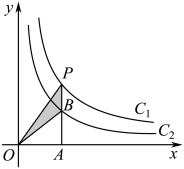 A、4 B、2 C、1 D、619. 如图,在平面直角坐标系中,的顶点 , 的坐标分别是 , , . 若函数( , )的图象经过点 , 则的值为( )
A、4 B、2 C、1 D、619. 如图,在平面直角坐标系中,的顶点 , 的坐标分别是 , , . 若函数( , )的图象经过点 , 则的值为( )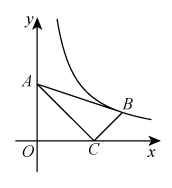 A、3 B、2 C、 D、20. 如图,在 中, , .将 绕点 逆时针方向旋转 ,得到 ,连接 .则线段 的长为( )
A、3 B、2 C、 D、20. 如图,在 中, , .将 绕点 逆时针方向旋转 ,得到 ,连接 .则线段 的长为( )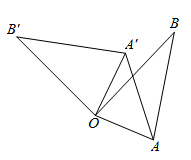 A、1 B、 C、 D、21. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、22. 如图,在中,点Р在边上,则在下列四个条件中:①;②;③;④ , 能满足与相似的条件以及性质的是( )
A、1 B、 C、 D、21. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、22. 如图,在中,点Р在边上,则在下列四个条件中:①;②;③;④ , 能满足与相似的条件以及性质的是( )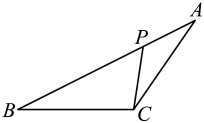 A、①②④ B、①③④ C、②③④ D、①②③23. 某超市购进一批商品,单价40元.经市场调查,销售定价为52元时,可售出180个,定价每增加1元,销售量减少10个,因受库存的影响,每批次进货个数不得超过180个,超市若将准备获利2000元,则定价为多少元?( )A、50 B、60 C、50或60 D、10024. 已知关于x的一元二次方程x2-kx+k-3=0的两个实数根分别为 ,且 ,则k的值是( )A、-2 B、2 C、-1 D、125. 如图,若 , , 与交于点 , 且 , , 则等于( )
A、①②④ B、①③④ C、②③④ D、①②③23. 某超市购进一批商品,单价40元.经市场调查,销售定价为52元时,可售出180个,定价每增加1元,销售量减少10个,因受库存的影响,每批次进货个数不得超过180个,超市若将准备获利2000元,则定价为多少元?( )A、50 B、60 C、50或60 D、10024. 已知关于x的一元二次方程x2-kx+k-3=0的两个实数根分别为 ,且 ,则k的值是( )A、-2 B、2 C、-1 D、125. 如图,若 , , 与交于点 , 且 , , 则等于( )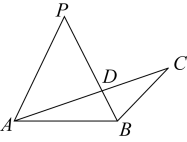 A、3 B、6 C、7 D、1226. 如图,在中,以为直径的分别与交于点F,D,点F是的中点,连接交于点E.若 . 连接 , 则弦的长为( )
A、3 B、6 C、7 D、1226. 如图,在中,以为直径的分别与交于点F,D,点F是的中点,连接交于点E.若 . 连接 , 则弦的长为( )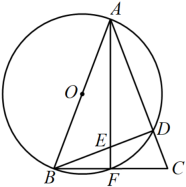 A、 B、 C、4 D、527. 反比例函数的图像与正比例函数的图像没有交点,若点 , , 在这个反比例函数的图象上,则下列结论中正确的是( )A、; B、; C、; D、 .28. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .
A、 B、 C、4 D、527. 反比例函数的图像与正比例函数的图像没有交点,若点 , , 在这个反比例函数的图象上,则下列结论中正确的是( )A、; B、; C、; D、 .28. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .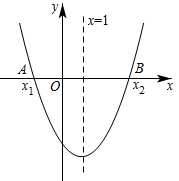
正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个二、解答题
-
29. 如图,反比例函数与一次函数的图像在第一象限交于、两点.
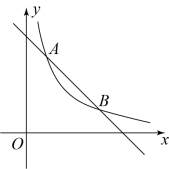 (1)、则 , ,(2)、观察图像,请直接写出满足的取值范围.(3)、若Q为y轴上的一点,使最小,求点Q的坐标.30. 如图,在中,为直径,弦与交于P点, .
(1)、则 , ,(2)、观察图像,请直接写出满足的取值范围.(3)、若Q为y轴上的一点,使最小,求点Q的坐标.30. 如图,在中,为直径,弦与交于P点, .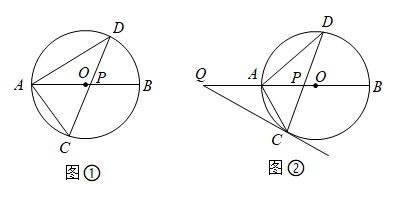 (1)、如图①,若 , 求的度数;(2)、如图②,过点C作的切线与BA的延长线交于点Q,若 , 求的度数.31. 在平面直角坐标系中,O为原点,点A(8,0),点B(0,6),把△ABO绕点B逆时针旋转得△A′B′O′,点A、O旋转后的对应点为A′、O′,记旋转角为α.
(1)、如图①,若 , 求的度数;(2)、如图②,过点C作的切线与BA的延长线交于点Q,若 , 求的度数.31. 在平面直角坐标系中,O为原点,点A(8,0),点B(0,6),把△ABO绕点B逆时针旋转得△A′B′O′,点A、O旋转后的对应点为A′、O′,记旋转角为α.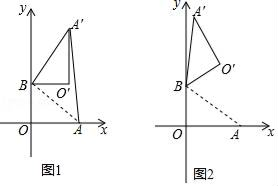 (1)、如图1,若α=90°,则AB= , 并求AA′的长;(2)、如图2,若α=120°,求点O′的坐标;(3)、在(2)的条件下,边OA上的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,直接写出点P′的坐标.32. 如图,在平面直角坐标系中,抛物线经过点 , 点M为抛物线的顶点,点B在y轴上,且 , 直线AB与抛物线在第一象限交于点 .
(1)、如图1,若α=90°,则AB= , 并求AA′的长;(2)、如图2,若α=120°,求点O′的坐标;(3)、在(2)的条件下,边OA上的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,直接写出点P′的坐标.32. 如图,在平面直角坐标系中,抛物线经过点 , 点M为抛物线的顶点,点B在y轴上,且 , 直线AB与抛物线在第一象限交于点 .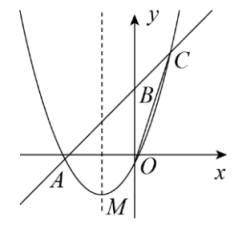 (1)、求抛物线的解析式:(2)、直线的函数解析式为 , 点M的坐标为 , 连接 , 若过点O的直线交线段于点P,将的面积分成的两部分,则点P的坐标为;(3)、在y轴上找一点Q,使得的周长最小,则点Q的坐标为
(1)、求抛物线的解析式:(2)、直线的函数解析式为 , 点M的坐标为 , 连接 , 若过点O的直线交线段于点P,将的面积分成的两部分,则点P的坐标为;(3)、在y轴上找一点Q,使得的周长最小,则点Q的坐标为