山西省晋中市2022-2023学年九年级上学期1月期末考试数学试题
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图的是( )A、
 B、
B、 C、
C、 D、
D、 2. 神奇的自然界处处隐含着数学美!生物学家在向日葵圆盘中发现:向日葵籽粒成螺线状排列,螺线的发散角是 . 我们知道圆盘一周为 , , . 这体现了( )
2. 神奇的自然界处处隐含着数学美!生物学家在向日葵圆盘中发现:向日葵籽粒成螺线状排列,螺线的发散角是 . 我们知道圆盘一周为 , , . 这体现了( ) A、轴对称 B、旋转 C、平移 D、黄金分割3. 用配方法解一元二次方程 时,此方程可变形为( )A、 B、 C、 D、4. 如图,是的直径, , 是上的两点,且 , 则的度数为( )
A、轴对称 B、旋转 C、平移 D、黄金分割3. 用配方法解一元二次方程 时,此方程可变形为( )A、 B、 C、 D、4. 如图,是的直径, , 是上的两点,且 , 则的度数为( )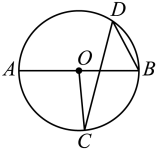 A、42° B、84° C、90° D、96°5. 将抛物线先向右平移1个单位长度,再向下平移5个单位长度,所得新抛物线的函数表达式为( )A、 B、 C、 D、6. 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球7. 大约在两千五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是9cm,则蜡烛火焰的高度是( )
A、42° B、84° C、90° D、96°5. 将抛物线先向右平移1个单位长度,再向下平移5个单位长度,所得新抛物线的函数表达式为( )A、 B、 C、 D、6. 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球7. 大约在两千五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是9cm,则蜡烛火焰的高度是( )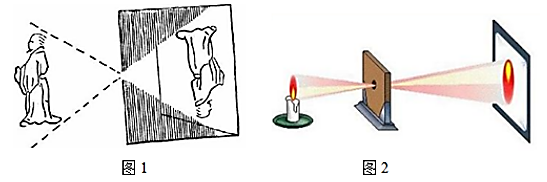 A、6cm B、8cm C、10cm D、12cm8. 对于反比例函数 , 下列说法正确的是( )A、函数图象分布在第一、三象限 B、点在该函数图象上 C、当时, D、当时,y随x的增大而增大9. 如图 , 与相交于点G,且 , 则=( )
A、6cm B、8cm C、10cm D、12cm8. 对于反比例函数 , 下列说法正确的是( )A、函数图象分布在第一、三象限 B、点在该函数图象上 C、当时, D、当时,y随x的增大而增大9. 如图 , 与相交于点G,且 , 则=( ) A、5:3 B、1:3 C、3:5 D、2:310. 如图,以等边三角形的一边为直径的半圆交边于点 , 交边于点 . 若 , 则图中阴影部分的面积为( )
A、5:3 B、1:3 C、3:5 D、2:310. 如图,以等边三角形的一边为直径的半圆交边于点 , 交边于点 . 若 , 则图中阴影部分的面积为( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11. 若反比例函数的图象分别位于第一、三象限,请写出一个满足条件的反比例函数表达式 . (写出一个即可)12. 已知 且 = ,则 为13. 某城市启动“城市森林”绿化工程,林业部门要考察某种树苗在一定条件下的移植成活率.在同样的条件下,对这种树苗进行大量移植,并统计成活情况,数据如下表所示:
移植数量/棵
10
270
400
750
1500
3500
7000
9000
14000
成活数量/棵
8
235
369
662
1335
3203
6335
8073
12628
成活率
0.800
0.870
0.923
0.883
0.890
0.915
0.905
0.897
0.902
由此估计这种树苗移植成活的概率为 . (结果精确到0.1)
14. 如图,李大斧要建一个矩形羊圈,羊圈的一边利用长为的住房墙,另外三边用长的彩钢围成,为了方便进出,在垂直于住房墙的一边留了一扇宽的门.若要使羊圈的面积为 , 则所围矩形与墙垂直的一边长为 .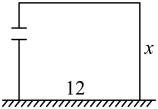 15. 如图,四边形是由两个直角三角板拼成的,其中 , , E为边的中点,连接 , 交于点F.若 , 则的长为 .
15. 如图,四边形是由两个直角三角板拼成的,其中 , , E为边的中点,连接 , 交于点F.若 , 则的长为 .
三、解答题
-
16. 解下列方程:(1)、;(2)、 .17. 在平面直角坐标系中,的位置如图所示,其中 , , .
 (1)、将向左平移6个单位长度,点 , , 的对应点分别为点 , , , 画出平移后得到的;(2)、将绕着点顺时针旋转90°,点 , , 的对应点分别为点 , , , 画出旋转后得到的 , 并直接写出点 , , 的坐标.18. 如图,已知一次函数的图象与反比例函数的图象交于 , B两点,点B的横坐标为 , 与x轴交于点C,连接 , .
(1)、将向左平移6个单位长度,点 , , 的对应点分别为点 , , , 画出平移后得到的;(2)、将绕着点顺时针旋转90°,点 , , 的对应点分别为点 , , , 画出旋转后得到的 , 并直接写出点 , , 的坐标.18. 如图,已知一次函数的图象与反比例函数的图象交于 , B两点,点B的横坐标为 , 与x轴交于点C,连接 , . (1)、k的值为 .(2)、求的面积.19. “二十大之后”,某校打算组织九年级名团员开展一次以“爱国教育”为主题的观影活动.目前有A《万里归途》;B《我和我的祖国》;C《长津湖之水门桥》三部电影可供选择,小华和小军参加了此次观影活动.(1)、小军选择看《万里归途》的概率为 .(2)、请用画树状图或列表的方法,求小华和小军恰好选择看同一部电影的概率.20. 如图,强强同学为了测量学校一棵笔直的大树OE的高度,先在操场上点A处放一面平面镜,从点A处后退1m到点B处,恰好在平面镜中看到树的顶部E点的像;再将平面镜向后移动4m(即AC=4m)放在C处,从点C处向后退1.5m到点D处,恰好再次在平面镜中看到大树的顶部E点的像,测得强强的眼睛距地面的高度FB、GD为1.5m,已知点O,A,B,C,D在同一水平线上,且GD⊥OD,FB⊥OD,EO⊥OD.求大树OE的高度.(平面镜的大小忽略不计)
(1)、k的值为 .(2)、求的面积.19. “二十大之后”,某校打算组织九年级名团员开展一次以“爱国教育”为主题的观影活动.目前有A《万里归途》;B《我和我的祖国》;C《长津湖之水门桥》三部电影可供选择,小华和小军参加了此次观影活动.(1)、小军选择看《万里归途》的概率为 .(2)、请用画树状图或列表的方法,求小华和小军恰好选择看同一部电影的概率.20. 如图,强强同学为了测量学校一棵笔直的大树OE的高度,先在操场上点A处放一面平面镜,从点A处后退1m到点B处,恰好在平面镜中看到树的顶部E点的像;再将平面镜向后移动4m(即AC=4m)放在C处,从点C处向后退1.5m到点D处,恰好再次在平面镜中看到大树的顶部E点的像,测得强强的眼睛距地面的高度FB、GD为1.5m,已知点O,A,B,C,D在同一水平线上,且GD⊥OD,FB⊥OD,EO⊥OD.求大树OE的高度.(平面镜的大小忽略不计) 21. 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.切割线定理揭示了从圆外一点引圆的切线和割线时,切线与割线之间的关系.
21. 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.切割线定理揭示了从圆外一点引圆的切线和割线时,切线与割线之间的关系.如图1,是外一点,切于点 , 交于点(即是的割线),则 .

下面是切割线定理的证明过程:
证明:如图2,连接并延长,交于点 , 连接 .
切于点 ,
.
.
是的直径,
……
(1)、根据前面的证明思路,补全剩余的证明过程;(2)、在图1中,已知 , , 则 , .22. 综合与实践九年级(1)班同学在数学老师的指导下,以“三角形的旋转”为主题,开展数学活动.
(1)、操作探究:
如图1,为等边三角形,将绕点旋转 , 得到 , 连接 , 则 . 若是的中点,连接 , 则与的数量关系是 .
(2)、迁移探究:如图2,(1)中的其他条件不变,当绕点逆时针旋转 , 得到 , 求出此时的度数及与的数量关系.
(3)、拓展应用:如图3,在中, , , 将绕点旋转,得到 , 连接 , 是的中点,连接 . 当时,求的长.
23. 综合与探究如图,抛物线与x轴交于 , 两点,与y轴交于点C.点是x轴上的一个动点,过点P作直线轴,与直线BC交于点M,与抛物线交于点N.
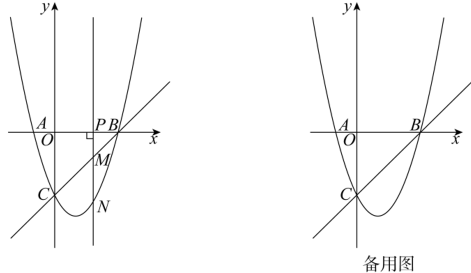 (1)、求这个抛物线的函数表达式.(2)、①若点P在线段OB上运动,求线段MN的最大值;
(1)、求这个抛物线的函数表达式.(2)、①若点P在线段OB上运动,求线段MN的最大值;②若点P在x轴的正半轴上运动,在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.