山东省聊城市经开区三校2022-2023学年九年级上学期期末考试数学试题
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列图形一定是相似图形( )A、两个菱形 B、两个矩形 C、两个直角三角形 D、两个等边三角形2.
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
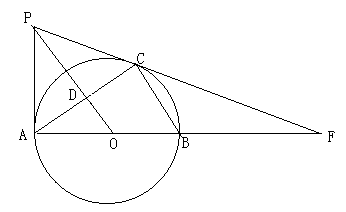
 A、3:4 B、9:16 C、9:1 D、3:13. 如图, 中, ,点 是 的内心,则 的度数为( )
A、3:4 B、9:16 C、9:1 D、3:13. 如图, 中, ,点 是 的内心,则 的度数为( ) A、 B、 C、 D、4. 在平面直角坐标系中,已知点 , , 以原点为位似中心,相似比为 , 把缩小,则点的对应点的坐标是( )A、 B、 C、或 D、或5. 下列方程中:①;②;③;④;⑤;⑥ . 一元二次方程共有( )个.A、1 B、2 C、3 D、46. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
A、 B、 C、 D、4. 在平面直角坐标系中,已知点 , , 以原点为位似中心,相似比为 , 把缩小,则点的对应点的坐标是( )A、 B、 C、或 D、或5. 下列方程中:①;②;③;④;⑤;⑥ . 一元二次方程共有( )个.A、1 B、2 C、3 D、46. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )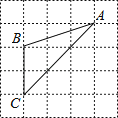 A、 B、 C、 D、7. 如图,下列各曲线中能够表示y是x的函数的是( ).A、
A、 B、 C、 D、7. 如图,下列各曲线中能够表示y是x的函数的是( ).A、 B、
B、 C、
C、 D、
D、 8. 若点、和分别在反比例函数的图象上,且 , 则下列判断中正确的是( )A、 B、 C、 D、9. 如图,正五边形 内接于 ,点 是劣弧 上一点(点 不与点 重合),则 ( )
8. 若点、和分别在反比例函数的图象上,且 , 则下列判断中正确的是( )A、 B、 C、 D、9. 如图,正五边形 内接于 ,点 是劣弧 上一点(点 不与点 重合),则 ( ) A、 B、 C、 D、10. 将抛物线向左平移2个单位长度,再向上平移2个单位长度,所得抛物线的解析式为( )A、 B、 C、 D、11. 已知关于x的一元二次方程有两个不相等的实数根,则k的取值范围为( )A、 B、且 C、且 D、12. 如图为二次函数y=ax2+bx+c (a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④ 当-1<x<3时,y>0 其中正确的个数为( )
A、 B、 C、 D、10. 将抛物线向左平移2个单位长度,再向上平移2个单位长度,所得抛物线的解析式为( )A、 B、 C、 D、11. 已知关于x的一元二次方程有两个不相等的实数根,则k的取值范围为( )A、 B、且 C、且 D、12. 如图为二次函数y=ax2+bx+c (a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④ 当-1<x<3时,y>0 其中正确的个数为( )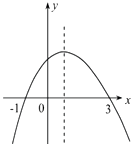 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 在中,若 , , 都是锐角,则是三角形.14. 如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是 米.
 15. 如图,ABC是一块锐角三角形的材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是mm.
15. 如图,ABC是一块锐角三角形的材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是mm. 16. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
16. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .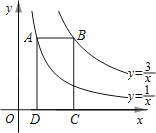 17. 如图,在中, , , , 将绕点A逆时针旋转后得到 , 点B经过的路径为 , 则图中阴影部分的面积为 .
17. 如图,在中, , , , 将绕点A逆时针旋转后得到 , 点B经过的路径为 , 则图中阴影部分的面积为 .
三、解答题
-
18. 计算:(1)、;(2)、 .19. 如图,AD是△ABC的中线, .求:
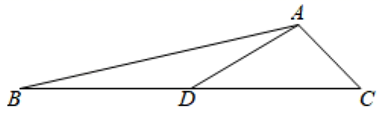 (1)、BC的长;(2)、∠ADC的正弦值.20. 2013年,东营市某楼盘以每平方米6500元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.(1)、求平均每年下调的百分率;(2)、假设2016年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)21. 如图,在平行四边形中,过点A作 , 垂足为E,连接 , F为线段上一点,且 .
(1)、BC的长;(2)、∠ADC的正弦值.20. 2013年,东营市某楼盘以每平方米6500元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.(1)、求平均每年下调的百分率;(2)、假设2016年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)21. 如图,在平行四边形中,过点A作 , 垂足为E,连接 , F为线段上一点,且 . (1)、求证: .(2)、若 , , , 求的长.22. 已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y= 图象的两个交点.
(1)、求证: .(2)、若 , , , 求的长.22. 已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y= 图象的两个交点. (1)、求一次函数和反比例函数的解析式;(2)、求△AOB的面积;(3)、观察图象,直接写出不等式kx+b﹣ >0的解集.23. 在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm.
(1)、求一次函数和反比例函数的解析式;(2)、求△AOB的面积;(3)、观察图象,直接写出不等式kx+b﹣ >0的解集.23. 在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm. (1)、求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1cm)(2)、求显示屏顶端A与底座C的距离AC.(结果精确到1cm)(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3, ≈1.4, ≈1.7)
(1)、求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1cm)(2)、求显示屏顶端A与底座C的距离AC.(结果精确到1cm)(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3, ≈1.4, ≈1.7)