内蒙古自治区包头市2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $\sqrt{3} x^{2} + 4 \sqrt{2} x = 2 \sqrt{3}$ 根的判别式 $Δ$ 的值为（）．

A、56 B、16 C、36 D、28

查看试题解析
2. 一个圆柱和正三棱柱组成的几何体如图水平放置，其主视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，值为 $\frac{1}{4}$ 的是（）．

A、 $s i n 45 ° \times c o s 45 °$ B、 $t a n 45 ° - c o s^{2} 30 °$ C、 $\frac{t a n 30 °}{c o s 60 °}$ D、 ${(t a n 60 °)}^{- 1}$

查看试题解析
4. 经过某十字路口的汽车，可能直行，也可能向左转或向右转，如果这三种可能性大小相同，那么两辆汽车经过这个十字路口时，第一辆车向左转，第二辆车向右转的概率是（）．

A、 $\frac{1}{3}$ B、 $\frac{1}{9}$ C、 $\frac{2}{9}$ D、 $\frac{4}{27}$

查看试题解析
5. 如图，某同学剪了两条宽均为 $\sqrt{3}$ 的纸条，交叉叠放在一起，且它们的交角为60°，则它们重叠部分的面积为（）．

A、3 B、 $2 \sqrt{3}$ C、 $3 \sqrt{6}$ D、6

查看试题解析
6. “跳眼法”是炮兵常用的一种简易测距方法，如图，点A为左眼，点B为右眼，点O为右手大拇指，点C为敌人的位置，点D为敌人正左侧方的某一个参照物 $(C D ∥ A B)$ ，已知大多数人的眼距长约为6.4厘米左右，而手臂长约为64厘米左右．若 $C D$ 的估测长度为50米，那么 $C O$ 的大致距离为（）米．

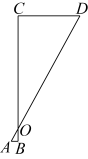A、250 B、320 C、500 D、750

查看试题解析
7. 已知二次函数 $y = a {(x - 2)}^{2} + 2 a (x - 2)$ （ $a$ 为常数， $a \neq 0$ ）当 $x = 1$ 时， $y > 0$ ，则该函数图象的顶点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 对于一元二次方程 $a x^{2} + b x + c = 0$ $(a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ $(a \neq 0)$ 必有两个不相等的实根；③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$ .

其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知反比例函数 $y = \frac{k}{x}$ （k为常数）的图象经过点 $B (- 3 ， 2)$ ．如图，过点B作直线 $A B$ 与函数 $y = \frac{k}{x}$ 的图象交于点A，与x轴交于点C，且 $A B = 2 B C$ ，过点A作直线 $A F ⊥ A B$ ，交x轴于点F，则线段 $A F$ 的长为（）

A、 $8 \sqrt{5}$ B、 $6 \sqrt{2}$ C、 $7 \sqrt{5}$ D、 $6 \sqrt{5}$

查看试题解析
10. 如图，在 $△ A B C$ 中，过点C作 $C D ⊥ A B$ ，垂足为点D，过点D分别作 $D E ⊥ A C$ ， $D F ⊥ B C$ ，垂足分别为E，F．连接EF交线段CD于点O，若 $C O = 2 \sqrt{2}$ ， $C D = 3 \sqrt{2}$ ，则 $E O \cdot F O$ 的值为（）．

A、 $6 \sqrt{3}$ B、4 C、 $5 \sqrt{6}$ D、6

查看试题解析

二、填空题

11. 在几何体三棱锥、圆柱、圆锥中，主视图为矩形的几何体为．

查看试题解析
12. 抛掷一枚质地均匀的普通硬币，正面朝上记2分，反面朝上记1分．小明抛掷这枚硬币两次，则两次分数之和不大于3的概率为．

查看试题解析
13. 如图，图形甲与图形乙是位似图形，O是位似中心，位似比为 $3 ： 5$ ，点A，B的对应点，分别为点 $A^{'}$ ， $B^{'}$ ．若 $A B = 6$ ，则 $A^{'} B^{'}$ 的长为．

查看试题解析
14. 已知点 $A (1 ， y_{1})$ ， $B (- 2 ， y_{2})$ ， $C (- 1 ， y_{3})$ ，在反比例函数 $y = \frac{- | k | - 2}{x}$ （k是常数）的图像上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系为．（用“＜”连接）

查看试题解析
15. 如图，坡角为 $α$ 的斜坡上有一棵垂直于水平地面的大树 $A B$ ，当太阳光线与水平线成 $45 °$ 角沿斜坡照下时，在斜坡上的树影 $B C$ 长为m，则大树 $A B$ 的高为．（请用含m， $α$ 的式子表示）

查看试题解析
16. 如图，在“黄金三角形” $A B C$ 中， $∠ A = 36 °$ ， $A B = A C$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D，若 $C D = 1$ ，则 $A C$ 的长为．

查看试题解析
17. 已知二次函数 $y = x^{2} + b x + c$ 的图象与x轴交于 $A (- 1 ， 0)$ 与 $B (5 ， 0)$ 两点，与y轴交于点C，若点P在该抛物线的对称轴上，则PA＋PC的最小值为．

查看试题解析
18. 如图，正方形 $A B C D$ 的边长为2，点E从点 $A$ 出发沿着线段 $A D$ 向点D运动（不与点A，D重合），同时点F从点D出发沿着线段 $D C$ 向点C运动（不与点D，C重合，点E与点F的运动速度相同． $B E$ 与 $A F$ 相交于点G，H为 $B F$ 中点、则有下列结论：
① $∠ B G F$ 是定值；② $F B$ 平分 $∠ A F C$ ；③当E运动到 $A D$ 中点时， $G H = \frac{\sqrt{5}}{2}$ ；④当 $A G + B G = \sqrt{6}$ 时，四边形 $G E D F$ 的面积是 $\frac{1}{2}$ ．其中正确的结论序号是．

查看试题解析

三、解答题

19. 解下列方程：

(1)、 $x^{2} + 2 \sqrt{5} x + 10 = 0$

(2)、 $4 {(2 y - 5)}^{2} = 9 {(3 y - 1)}^{2}$

查看试题解析
20. 一个不透明的口袋中有4个完全相同的小球，球上分别标有数字-2，0，1，4

(1)、若随机摸出一个小球记作m，然后放回，再随机摸出一个小球记作n，请用画树状图法或列表法，求方程 $m x^{2} - 2 x + n = 0$ 是关于x的一元二次方程且此方程无解的概率；

(2)、若改为不放回抽样，随机摸出一个小球记作m，然后不放回，再随机摸出一个小球记作n，请用画树状图法或列表法，求在点 $(m ， n)$ 在反比例函数的图象 $y = - \frac{1}{x}$ 的概率．

查看试题解析
21. 某小区拟建设地下停车库入口，将原步行楼梯入口AC改造为斜坡AD．已知入口高AB＝3m，坡面AC的坡度i＝1：1，新坡面坡角∠ADB＝30°．

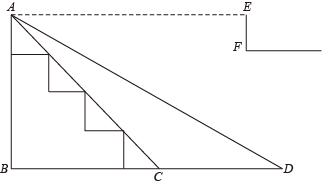(1)、求斜坡底部增加的长度CD为多少米？（保留根号）

(2)、入口处水平线AE＝5m，地下停车库坡道入口上方点E处有悬挂广告牌EF，EF⊥BD，EF＝0.5m．若一辆高度为2米的货车沿斜坡AD驶入车库，行进中是否会碰到广告牌的下端F？请说明理由．（参考数据： $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7）

查看试题解析
22. 某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．

(1)、求该种水果每次降价的百分率；

(2)、从第一次降价的第1天算起，第 $x$ 天（ $x$ 为整数）的售价、销量及储存和损耗费用的相关信息如表所示．
时间 $x$ （天）
$1 \leq x < 9$
$9 \leq x < 15$
售价（元/斤）
第1次降价后的价格
第2次降价后的价格
销量（斤）
$80 - 3 x$
$120 - x$
储存和损耗费用（元）
$40 + 3 x$
$3 x^{2} - 64 x + 400$
已知该种水果的进价为4.1元/斤，设销售该水果第 $x$ （天）的利润为 $y$ （元），求 $y$ 与 $x$ （ $1 \leq x < 15$ ）之间的函数解析式，并求出第几天时销售利润最大．

查看试题解析
23. 如图，一次函数 $y = 2 x + b$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像交于点 $A (1 ， 4)$ ，与 $y$ 轴交于点 $B$ ．

(1)、k= ， b=；

(2)、连接并延长 $A O$ ，与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像交于点 $C$ ，点 $D$ 在 $y$ 轴上，若以 $O$ 、 $C$ 、 $D$ 为顶点的三角形与 $△ A O B$ 相似，求点 $D$ 的坐标．

查看试题解析
24. 如图1，在矩形 $A B C D$ 中， $B G ⊥ A C$ 交 $A C$ 于点G，E为 $A B$ 的中点， $E G$ 的延长线交 $A D$ 于点F，连接 $C F$ ．

(1)、若 $A F = F D$ ，证明： $△ E A F ∽ △ A B C$ ；

(2)、在（1）的条件下，求 $t a n ∠ A B G$ 的值；

(3)、如图2，若 $∠ E F C = 90 °$ ， M为 $C D$ 的中点，连接 $B F$ ， $F M$ ﹒已知 $A B = \sqrt{k} A D$ ．
①求证： $B F ⊥ F M$ ；

②求k的值．

查看试题解析
25. 抛物线 $y = x^{2} + b x + c$ 与x轴交于A、B两点（A在B的左侧），与y轴交于点 $C (0 ， - 4)$ ，已知 $c o s ∠ A B C = \frac{\sqrt{2}}{2}$ ，点P在抛物线上，连接 $B C 、 B P$ ．

(1)、求抛物线的解析式；

(2)、如图1，若点P在第四象限，点D在线段 $B C$ 上，连接 $P D$ 并延长交x轴于点E，连接 $C E$ ，记 $△ D C E$ 的面积为 $S_{1}$ ， $△ D B P$ 的面积为 $S_{2}$ ，当 $S_{1} = S_{2}$ 时，求点P的坐标；

(3)、如图2，若点P在第二象限，点F为抛物线的顶点，抛物线的对称轴l与线 $B C$ 交于点G，当 $∠ P B C + ∠ C F G = 90 °$ 时，求点P的横坐标．

查看试题解析

时间 $x$ （天）	$1 \leq x < 9$	$9 \leq x < 15$
售价（元/斤）	第1次降价后的价格	第2次降价后的价格
销量（斤）	$80 - 3 x$	$120 - x$
储存和损耗费用（元）	$40 + 3 x$	$3 x^{2} - 64 x + 400$