辽宁省大连市高新园区2022-2023学年九年级上学期期末考试数学试题

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $A B = 5$ ，则 $s i n B$ 的值是（）

A、 $\frac{3}{5}$ B、 $\frac{3}{4}$ C、 $\frac{5}{3}$ D、 $\frac{4}{3}$

查看试题解析
3. 与点 $A (1 ， - 2)$ 关于原点对称的点 $B$ 的坐标是（）

A、 $（ 2 ， 1 ）$ B、 $（ 1 ， 2 ）$ C、 $（ - 2 ， 1 ）$ D、 $（ - 1 ， 2 ）$

查看试题解析
4. 用配方法解方程 $x^{2} - 4 x + 2 = 0$ ，下列配方正确的是（）

A、 ${(x - 2)}^{2} = 0$ B、 ${(x + 2)}^{2} = 2$ C、 ${(x - 2)}^{2} = - 2$ D、 ${(x - 2)}^{2} = 2$

查看试题解析
5. 如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 、 $B C$ 是 $⊙ O$ 的弦，若 $∠ A = 20 °$ ，则 $∠ B$ 的度数为（）

A、 $80 °$ B、 $70 °$ C、 $60 °$ D、 $50 °$

查看试题解析
6. 将抛物线 $y = 2 {(x - 3)}^{2} + 2$ 向左平移2个单位，再向上平移3个单位，平移后所得抛物线的解析式为（）

A、 $y = 2 {(x - 5)}^{2} + 5$ B、 $y = 2 x^{2}$ C、 $y = 2 {(x - 1)}^{2} + 5$ D、 $y = 2 {(x - 1)}^{2} - 1$

查看试题解析
7. 在一个不透明的袋子里装有红球6个、黄球4个，这些球除颜色外都相同．小明从袋子中摸一次，摸到黄球的概率是（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{3}$ D、 $\frac{3}{10}$

查看试题解析
8. 关于 $x$ 的一元二次方程 $x^{2} - 2 x + k = 0$ 有两个实数根，则 $k$ 的取值范围是（）

A、 $k \geq 1$ B、 $k \leq 1$ C、 $k \geq - 1$ D、 $k < 1$

查看试题解析
9. 如图，在 $△ A B C$ 中，以 $C$ 为圆心，适当长为半径画弧，分别交 $A C 、 B C$ 于点 $E 、 F$ ，再分别以 $E 、 F$ 为圆心，大于 $\frac{1}{2} E F$ 的长为半径画弧，两弧相交于点 $N$ ．连结 $C N$ 交 $A B$ 于点 $D$ ，过 $D$ 作 $B C$ 的平行线交 $A C$ 于 $M$ ，若 $B C = 3$ ， $A C = 2$ ，则 $D M =$ （）

A、 $\frac{5}{6}$ B、 $\frac{6}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
10. 如图，小强在某次投篮中，球的运动路线是抛物线 $y = - \frac{1}{5} x^{2} + 3.5$ 的一部分，若命中篮圈中心，则他与篮筐底的距离 $l$ 是（）

A、3m B、3.5m C、4m D、4.5m

查看试题解析

二、填空题

11. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + c = 0$ 的一个根为 $- 1$ ，则另一个根是．

查看试题解析
12. 对于二次函数 $y = {(x - 2)}^{2} + 1$ ，当 $x > 3$ 时， $y$ 随 $x$ 的增大而（填“增大”或“减小”）．

查看试题解析
13. 从n个苹果和3个桔子中任选1个，若选中苹果的概率是 $\frac{2}{3}$ ，则n的值为．

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中，点E在边 $B C$ 上， $D E$ 交对角线 $A C$ 于F，若 $C E = 2 B E$ ， $△ C E F$ 的面积等于 $4$ ，那么 $△ A F D$ 的面积等于．

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A B = 2$ $\sqrt{3}$ ，以点A为圆心， $A D$ 长为半径画弧交 $B C$ 于点E，连接 $A E$ ， $∠ B A E = 30 °$ ，则阴影部分的面积为．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A B = A C = a$ ，将 $A B C$ 绕点 $B$ 逆时针旋转得到 $△ D B E$ ，若点 $E$ 恰好为 $A C$ 的中点，则 $B C$ 的长为（用含 $a$ 的代数式表示）．

查看试题解析

三、解答题

17. 小明用描点法画抛物线

y = - x^{2} + 4 x - 3

．

(1)、请帮小明完成下面的表格，并根据表中数据在所给的平面直角坐标系中描点，连线从而画出此抛物线；

x	…	-1	0	1	2	3	4	5	…
$y = - x^{2} + 4 x - 3$	…	-8		0			-3	-8	…

(2)、直接写出抛物线的对称轴，顶点坐标．

查看试题解析

18. 某景区检票口有A，B，C共3个检票通道，甲，乙两人到该景区游玩，两人分别从3个检票通道中随机选择一个检票.

(1)、甲选择A检票通道的概率是；

(2)、求甲，乙两人选择的检票通道恰好相同的概率.

查看试题解析
19. 如图，在 $△ A B C$ 中，点D在 $B C$ 边上， $∠ A D C = ∠ B A C$ ， $C D = 1$ ， $B D = 3$ ，求 $A C$ 的长．

查看试题解析
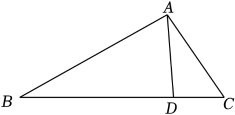20. 疫情期间“停课不停学”，辽宁省初中数学学科开通公众号进行公益授课，9月份该公众号关注人数为5000人，11月份该公众号关注人数达到7200人，若从9月份到11月份，每月该公众号关注人数的平均增长率相同，求该公众号关注人数的月平均增长率．

查看试题解析
21. 数学兴趣小组测量建筑物 $A B$ 的高度．如图，在建筑物 $A B$ 前方搭建高台 $C D$ 进行测量．高台 $C D$ 到 $A B$ 的距离 $B C$ 为6米，在高台顶端D处测得点A的仰角为 $40 °$ ，测得点B的俯角为 $30 °$ ．（参考数据： $s i n 40 ° \approx 0.64$ ， $c o s 40 ° \approx 0.77$ ， $t a n 40 ° \approx 0.84$ ， $\sqrt{3} \approx 1.732$ ）

(1)、填空： $∠ A D B =$ $°$ ；

(2)、求建筑物 $A B$ 的高度（结果保留整数）．

查看试题解析
22. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆， $A B$ 是 $⊙ O$ 的直径，过O作 $O D ⊥ A C$ 于点E，延长 $O E$ 至点D，连结 $C D$ ，使 $∠ D = ∠ A$ ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线；

(2)、若 $A B = C D = 2 \sqrt{5}$ ，求 $A C$ 的长．

查看试题解析
23. 某公司研发了一款成本为30元的新型产品，投放市场进行销售．按照物价部门规定，销售单价不低于成本且不高于70元，调研发现每天的销售量y（个）与销售单价x（元）满足一次函数关系，其图象如图所示．

(1)、求每天的销售量y（个）与销售单价x（元）的函数关系式；

(2)、销售单价为多少元时，每天获得的利润最大，最大利润是多少元？

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， A C = 8 c m ， B C = 6 c m$ ． D为 $A C$ 中点，过D作 $D E ⊥ A C$ 交 $A B$ 于点E．动点P从点D出发，沿射线 $D E$ 以 $1 c m / s$ 的速度运动．过D作 $D M ∥ A B$ ，过P作 $P M ⊥ D M$ 于点M．设点P的运动时间为t（s）． $△ P D M$ 与 $△ A B C$ 重叠部分图形的面积为 $S (c m^{2})$ ．

(1)、当点M落在 $B C$ 边上时，求t的值；

(2)、当点M在 $△ A B C$ 内部时，求S关于t的函数解析式，并直接写出自变量t的取值范围．

查看试题解析
25. 综合与实践
问题情境：数学活动课上，王老师出示了一个问题：如图1，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 在 $B C$ 边上， $A D = A E$ ， $∠ A D E = \frac{1}{2} ∠ B A C$ ，延长 $B A$ 至点 $F$ ，连结 $E F$ ．求证： $∠ D A C = ∠ E A F$ ．

(1)、独立思考：请解答王老师提出的问题．

(2)、实践探究：在原有问题条件不变的情况下，王老师增加下面的条件，并提出新问题，请你解答．
“如图2，连结 $B E$ 交 $A C$ 于 $G$ ，若 $∠ A G E = ∠ G E F$ ， $A B = A F$ ，求证 $A G = \frac{1}{2} C D$ ． ”

(3)、问题解决：数学活动小组同学解决完上述问题后，感悟了此题的数学思想方法，对此题进行变式，提出新的问题，请你解答．
“如图3，在 $△ A B C$ 中， $A B = \frac{3}{2} A C$ ．点 $D$ 在 $B C$ 边上，点 $F$ 在 $△ A B C$ 内． $A D = \frac{3}{2} A F$ ， $∠ D A F = ∠ A D C$ ， $∠ A D B = ∠ B A C$ ，连结 $B F$ 交 $A D$ 于点 $E$ ，求 $\frac{A E}{C D}$ 的值”．

查看试题解析
26. 如图，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 与 $x$ 轴交于点 $A (- 1 ， 0)$ 和点 $B$ ，与 $y$ 轴交于点 $C (0 ， - 2)$ ，连接 $A C$ ， $B C$ ．

(1)、求抛物线的解析式；

(2)、点 $P$ 在第四象限的抛物线上，设 $△ A B C$ 的面积为 $S_{1}$ ， $△ P B C$ 的面积为 $S_{2}$ ，当 $S_{2} =$ $\frac{4}{5}$ $S_{1}$ 时，求点 $P$ 的坐标；

(3)、点 $M$ 在抛物线上，当 $∠ M A B = 2 ∠ A C O$ 时，求点 $M$ 的横坐标．

查看试题解析