吉林省长春市净月区2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \geq 0$ B、 $x \leq 2$ C、 $x \geq 2$ D、 $x \leq 0$

查看试题解析
2. 如图，△ABC中，∠ACB=90°，∠B=55°，点D是斜边AB的中点，那么∠ACD的度数为（）

A、15° B、25° C、35° D、45°

查看试题解析
3. 如图，在△ABC中，DE//BC， $\frac{A D}{B D}$ =2，若AE=6，则EC的值为（）

A、3 B、2 C、1 D、9

查看试题解析
4. 若 $3 a = 2 b$ ，则 $\frac{a}{b} =$ （）

A、 $\frac{3}{2}$ B、 $- \frac{3}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
5. 在Rt△ABC中，∠C＝90°，AB＝4，BC＝3，则sin∠B的值为（）

A、 $\frac{\sqrt{7}}{4}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{7}}{5}$

查看试题解析
6. 南宋著名数学家杨辉所著的《杨辉算法》中记载：“直田积八百六十四步，只云长阔共六十步，问长阔各几何？”意思是“一块矩形田地的面积是864平方步，只知道它的长与宽的和是60步，问它的长和宽各是多少步？”设矩形田地的长为x步，根据题意可以列方程为（）

A、 $x^{2} - 60 x - 864 = 0$ B、 $x (x + 60) = 864$ C、 $x^{2} - 60 x + 864 = 0$ D、 $x (x + 30) = 864$

查看试题解析
7. 已知二次函数 $y = a x^{2} + b x + c$ 的部分图像如图所示，当y>0时，x的取值范围是（）

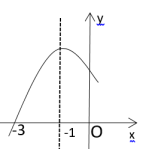A、x>-3 B、-3<x<1 C、x<-3或x>1 D、x<1

查看试题解析
8. 如图，在 $△ A B C$ ， $∠ B = 60 ° ， A B = 6 ， B C = 8$ ．将 $△ A B C$ 沿图中的 $D E$ 剪开．剪下的阴影三角形与原三角形不相似的是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

9. $\sqrt{125} =$ ．

查看试题解析
10. 若关于x的方程 $x^{2} - 4 x + k - 1$ 有两个不相等的实数根，则k的取值范围是．

查看试题解析
11. 已知 $A (- 2 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (5 ， y_{3})$ 都在二次函数 $y = - x^{2} + 2 x + k$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 从小到大排序为．

查看试题解析
12. 制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是元．

查看试题解析
13. 如图，已知线段 $A B$ 和线段 $C D$ 是第一象限内以原点O为位似中心的位似图形，A点坐标为 $(8 ， 12)$ ， C点坐标 $(2 ， 3)$ ，则线段 $A B$ 和线段 $C D$ 的数量关系为．

查看试题解析
14. 如图，把抛物线y= $\frac{1}{2}$ x²平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y= $\frac{1}{2}$ x²交于点Q，则图中阴影部分的面积为．

查看试题解析

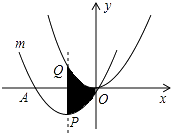
三、解答题

15. 计算： $\sqrt{2} + 2 s i n 45 ° + 3 t a n 30 ° - \sqrt{12}$ ．

查看试题解析
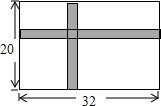
16. 解方程： $x^{2} - 7 x + 5 = 0$ ．

查看试题解析
17. 一个不透明的盒子里装有除颜色外其余均相同的2个黑球和n个白球，搅匀后从盒子里随机摸出一个球，摸到白球的概率为 $\frac{1}{3}$ ．

(1)、求n的值；

(2)、所有球放入盒中，搅匀后随机从中摸出1个球，放回搅匀，再随机摸出第2个球，求两次摸球摸到一个白球和一个黑球的概率，请用画树状图或列表的方法进行说明．

查看试题解析
18. 校生物小组有一块长32m，宽20m的矩形实验田，为了管理方便，准备沿平行于两边的方向纵、横个开辟一条等宽的小道，要使种植面积为540m² ，小道的宽应是多少米？

查看试题解析
19. 如图，在4×4的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点成为格点，点A、B、C均为格点，只用无刻度的直尺，按下列要求作图．

(1)、在图①中，在 $A C$ 上找一点D，使 $S_{△ A B D} = S_{△ B C D}$ ；

(2)、在图②中，在 $A C$ 上找一点E，使 $S_{△ A B E} ： S_{△ B C E} = 2 ： 3$ ；

(3)、在图③中，在 $△ A B C$ 内部找一点F，使 $S_{△ A C F} ： S_{△ A B F} ： S_{△ B C F} = 4 ： 3 ： 3$ ．

查看试题解析
20. 如图，在平行四边形 $A B C D$ 中，E为 $B C$ 边上一点，连接 $D E$ ， F为线段 $D E$ 上一点，且 $∠ A F E = ∠ B$ ．

(1)、求证： $△ A D F ∽ △ D E C$ ；

(2)、连接 $A E$ ，当 $△ A B E$ 为直角三角形时， $A B = 8$ ， $A D = 6 \sqrt{3}$ ， $A F = 4 \sqrt{3}$ ， $s i n ∠ A B E =$ ．

查看试题解析
21. 图1是一种三角车位锁，其主体部分是由两条长度相等的钢条组成．当位于顶端的小挂锁打开时，钢条可放入底盒中（底盒固定在地面下），此时汽车可以进入车位；当车位锁上锁后，钢条按图1的方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位．图2是其示意图，经测量，钢条， $A B = A C = 50 c m$ ， $∠ A B C = 47 °$ ．

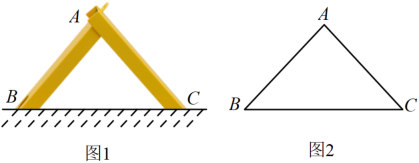(1)、求车位锁的底盒长 $B C$ ；

(2)、若一辆汽车的底盘高度为 $35 c m$ ，当车位锁上锁时，问这辆汽车能否进入该车位？通过计算说明理由．（参考数据： $s i n 47 ° \approx 0.73$ ， $c o s 47 ° \approx 0.68$ ， $t a n 47 ° \approx 1.07$ ）

查看试题解析
22. 如图：

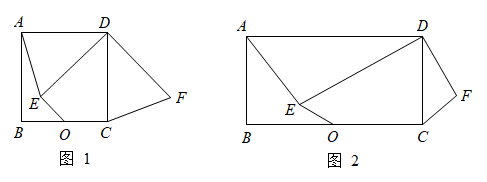(1)、【感知】如图1，正方形 $A B C D$ ， $A B = 2 \sqrt{5}$ ， O是 $B C$ 中点，点E为正方形内一点，且 $O E = 2$ ，连接 $A E$ 、 $D E$ ，将线段 $D E$ 绕点D逆时针旋转 $90 °$ 得到 $E F$ ，连接 $C F$ ．易证 $△ A E D ≌ △ C F D$ （无需证明）．

(2)、【探究】如图2，若将正方形 $A B C D$ 变为矩形 $A B C D$ ， $A D = 2 A B = 4 \sqrt{5}$ ， O是 $B C$ 中点，点E为矩形形内的一点，且 $O E = 2$ ，连接 $A E$ 、 $D E$ ，作 $D F ⊥ D E$ ，且 $D F = \frac{1}{2} D E$ ，连接 $C F$ ．求证： $△ A E D ∽ △ C F D$ ．

(3)、【应用】如图2，在探究的结论下，直接写出点F到 $C D$ 的最短距离 $d =$ ．

查看试题解析
23. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象过点 $(- 1 ， 0)$ ， $(0 ， 3)$ ， $(1 ， 4)$ ．

(1)、求二次函数的解析式；

(2)、当 $- 1 \leq x \leq 2$ 时，求函数y的最大值和最小值；

(3)、当 $- 1 \leq x \leq m$ 时，函数y的取值范围为 $0 \leq y \leq 4$ ，求m的取值范围；

(4)、点M的坐标为 $(n ， 2)$ ，点N的坐标为 $(n + 4 ， 2)$ ，若线段 $M N$ 与该函数图象恰有一个交点，直接写出n的取值范围．

查看试题解析
24. 在矩形 $A B C D$ 中， $A B = 6$ ， $A D = 8$ ，点P是线段 $B D$ 上的一个动点（不与点B、D重合），过点P作 $P E ⊥ B D$ ，交射线 $D C$ 于E，连接 $B E$ ．

(1)、矩形对角线 $B D$ 的长；

(2)、当点E与点C重合时，求 $D P$ 的长；

(3)、当直线 $B E$ 与直线 $A D$ 交于点F时，设 $P D = x$ ， $A F = y$ ．
①求y关于x的函数关系式，并写出x的取值范围；
②如果 $△ B P E$ 与 $△ B A F$ 相似，直接写出 $B P$ 的长．

查看试题解析