河北省邢台市广宗县2022-2023学年九年级上学期1月期末考试数学试题
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 如图所示,表示两棵小树在同一时刻阳光下的影子的图形可能是( )A、
 B、
B、 C、
C、 D、
D、 2. 二次函数化为的形式,下列正确的是( )A、 B、
2. 二次函数化为的形式,下列正确的是( )A、 B、 C、
D、
3. 在反比例函数 图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )A、k>3 B、k>0 C、k<3 D、k<04. 矩形的长为x,宽为y,面积为9,则y与x之间的函数关系式用图象表示大致为( )A、
C、
D、
3. 在反比例函数 图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )A、k>3 B、k>0 C、k<3 D、k<04. 矩形的长为x,宽为y,面积为9,则y与x之间的函数关系式用图象表示大致为( )A、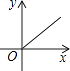 B、
B、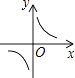 C、
C、 D、
D、 5. 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为( )
5. 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为( )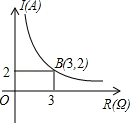 A、 B、 C、 D、6. 下列事件属于必然事件的是( )A、经过有交通信号的路口,遇到红灯 B、任意买一张电影票,座位号是双号 C、向空中抛一枚硬币,不向地面掉落 D、三角形中,任意两边之和大于第三边7. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )
A、 B、 C、 D、6. 下列事件属于必然事件的是( )A、经过有交通信号的路口,遇到红灯 B、任意买一张电影票,座位号是双号 C、向空中抛一枚硬币,不向地面掉落 D、三角形中,任意两边之和大于第三边7. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( ) A、8cm B、5cm C、3cm D、2cm8. 如图,在⊙O中, = ,∠AOB=40°,则∠ADC的度数是( )
A、8cm B、5cm C、3cm D、2cm8. 如图,在⊙O中, = ,∠AOB=40°,则∠ADC的度数是( ) A、40° B、30° C、20° D、15°9. 已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为( )
A、40° B、30° C、20° D、15°9. 已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为( )
A、相交 B、相切 C、相离 D、无法确定10. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )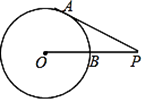 A、3 B、3 C、6 D、911. 如图,正方形ABCD内接于圆O,AB=4,则图中阴影部分的面积是( )
A、3 B、3 C、6 D、911. 如图,正方形ABCD内接于圆O,AB=4,则图中阴影部分的面积是( ) A、 B、 C、 D、12. 将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A、y=2x2+1 B、y=2x2﹣3 C、y=2(x﹣8)2+1 D、y=2(x﹣8)2﹣313. 如图, 抛物线的对称轴是直线 , 且经过点 , 则 的值为( )
A、 B、 C、 D、12. 将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A、y=2x2+1 B、y=2x2﹣3 C、y=2(x﹣8)2+1 D、y=2(x﹣8)2﹣313. 如图, 抛物线的对称轴是直线 , 且经过点 , 则 的值为( ) A、0 B、-1 C、1 D、214. 已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为( )
A、0 B、-1 C、1 D、214. 已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为( )
A、32 B、8 C、4 D、1615. 如图,已知 ABC , 任取一点O , 连AO , BO , CO , 分别取点D , E , F , 使OD= AO , OE= BO , OF= CO , 得 DEF . 下列说法中,错误的是( ) A、 DEF与 ABC是位似三角形 B、 OAC与 ODF是位似三角形 C、 DEF与 ABC周长的比是1:3 D、图中位似的两个三角形面积比是1:916. 如图, 的顶点是正方形网格的格点,则 的值为( )
A、 DEF与 ABC是位似三角形 B、 OAC与 ODF是位似三角形 C、 DEF与 ABC周长的比是1:3 D、图中位似的两个三角形面积比是1:916. 如图, 的顶点是正方形网格的格点,则 的值为( )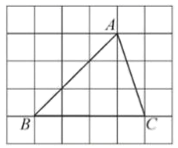 A、 B、 C、 D、17. 如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m , 测得AB=1.6m . BC=12.4m . 则建筑物CD的高是( )
A、 B、 C、 D、17. 如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m , 测得AB=1.6m . BC=12.4m . 则建筑物CD的高是( ) A、9.3m B、10.5m C、12.4m D、14m18. 在一个不透明的袋子中装有n个小球,这些球除颜色外均相同,其中红球有2个,如果从袋子中随机摸出一个球,这个球是红球的概率为 ,那么n的值是( )
A、9.3m B、10.5m C、12.4m D、14m18. 在一个不透明的袋子中装有n个小球,这些球除颜色外均相同,其中红球有2个,如果从袋子中随机摸出一个球,这个球是红球的概率为 ,那么n的值是( )
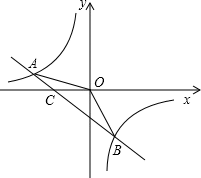
A、6 B、7 C、8 D、919. 如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2= (c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )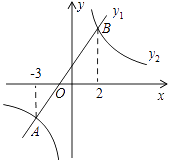 A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<220. 反比例函数的图象经过点P(3,-4),则这个反比例函数的解析式为( )A、 B、 C、 D、21. 如图,直线y=kx-3(k≠0)与坐标轴分别交于点C,B,与双曲线y=-(x<0)交于点A(m,1),则AB的长是( )
A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<220. 反比例函数的图象经过点P(3,-4),则这个反比例函数的解析式为( )A、 B、 C、 D、21. 如图,直线y=kx-3(k≠0)与坐标轴分别交于点C,B,与双曲线y=-(x<0)交于点A(m,1),则AB的长是( ) A、2 B、 C、2 D、22. 如图,是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的主视图(从正面看)是( )
A、2 B、 C、2 D、22. 如图,是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的主视图(从正面看)是( ) A、
A、 B、
B、 C、
C、 D、
D、 23. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )
23. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )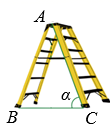 A、 米 B、 米 C、 米 D、 米24. 如图是一个以O为对称中心的中心对称图形,若∠A=30°,∠C=90°,AC=1,则AB的长为( )
A、 米 B、 米 C、 米 D、 米24. 如图是一个以O为对称中心的中心对称图形,若∠A=30°,∠C=90°,AC=1,则AB的长为( ) A、4 B、 C、 D、25. 如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B'位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )
A、4 B、 C、 D、25. 如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B'位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( ) A、50° B、60° C、70° D、80°
A、50° B、60° C、70° D、80°二、填空题
-
26. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.27. 如图,在直角坐标系中,与是位似图形,则位似中心的坐标为 .
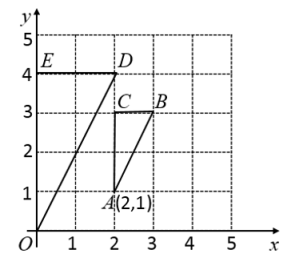 28. 如图,在中,点D,E分别为边 , 上的点,试添加一个条件: , 使得与相似.(任意写出一个满足条件的即可)
28. 如图,在中,点D,E分别为边 , 上的点,试添加一个条件: , 使得与相似.(任意写出一个满足条件的即可) 29.
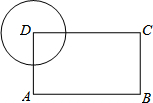
29.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
 30. 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是 cm2 .
30. 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是 cm2 .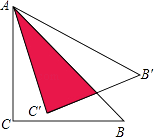
三、解答题
-
31. 解方程:32. 如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在太阳光下的投影BC=3m.
 (1)、请你在图中画出此时DE在阳光下的投影;(2)、在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,计算DE的长
(1)、请你在图中画出此时DE在阳光下的投影;(2)、在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,计算DE的长