河北省邯郸市广平县2022-2023学年九年级上学期期末考试数学试题

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列条件中，能确定一个圆的是（）

A、经过已知点M B、以点O为圆心， $10 c m$ 长为半径 C、以 $10 c m$ 长为半径 D、以点O为圆心

查看试题解析
2. 下列一元二次方程中，一次项系数为3的是（）

A、 $2 x^{2} + 3 x - 1 = 0$ B、 $x^{2} + 3 = 0$ C、 $2 x^{2} - 3 x - 1 = 0$ D、 $3 x^{2} + 2 x - 1 = 0$

查看试题解析
3. 已知反比例函数 $y = \frac{n - 2}{x}$ 的图象位于第一、三象限，则 $n$ 的取值可以是（）

A、-2 B、1 C、2 D、3

查看试题解析
4. 已知 $5 a = 2 b (a \neq 0 ， b \neq 0)$ ，下列变形错误的是（）

A、 $\frac{b}{a} = \frac{2}{5}$ B、 $\frac{b}{a} = \frac{5}{2}$ C、 $\frac{a}{2} = \frac{b}{5}$ D、 $\frac{a}{b} = \frac{2}{5}$

查看试题解析
5. 某斜坡的坡度 $i = 1$ ，则它的坡角是（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $75 °$

查看试题解析
6. 如果一个扇形的圆心角扩大为原来的2倍，半径扩大为原来的3倍，那么这个扇形的面积将扩大为原来的倍数是（）

A、18 B、12 C、6 D、4

查看试题解析
7. 把 $△ A B C$ 放大为原图形的2倍得到 $△ A^{'} B^{'} C^{'}$ ，则位似中心可以是（）

A、G点 B、F点 C、E点 D、D点

查看试题解析
8. 一司机驾驶汽车从甲地去乙地，他以80千米/时的平均速度用了6小时到达目的地，当他按原路匀速返回时，汽车的速度v（千米/时）与时间t（小时）的函数关系为（　　）

A、v＝ $\frac{480}{t}$ B、v+t＝480 C、v＝ $\frac{80}{t}$ D、v＝ $\frac{t - 6}{t}$

查看试题解析
9. 已知从点B观测热气球A的俯角为 $32 °$ ，从点C观测热气球A的仰角为 $58 °$ ，则两条视线的夹角 $∠ B A C$ 的度数是（）

A、 $110 °$ B、 $100 °$ C、 $90 °$ D、 $80 °$

查看试题解析
10. 下表记录了甲、乙、丙、丁四名同学参加某区“十九届六中全会”为主题的演讲比赛的相关数据：根据表中数据，从平均成绩优秀且成绩稳定的角度，选择甲同学参加市级比赛，则可以判断a、b的值可能是（）

甲
乙
丙
丁
平均数（分）
$a$
80
90
80
方差
$b$
2.2
5.4
2.4

A、95，6 B、95，2 C、85，2 D、85，6

查看试题解析
11. 以O为中心点的量角器与直角三角板 $A B C$ 按如图方式摆放，量角器的0刻度线与斜边 $A B$ 重合．点D为斜边 $A B$ 上一点，作射线 $C D$ 交弧 $A B$ 于点E，如果点E所对应的量角器上的读数为 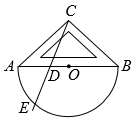$50 °$ ，那么 $∠ A C E$ 的大小为（）

A、 $35 °$ B、 $30 °$ C、 $25 °$ D、 $20 °$

查看试题解析
12. 如图是嘉淇用配方法解一元二次方程的具体过程，老师说这个解法出现了错误，则开始出现错误的步骤是（）

A、② B、③ C、④ D、⑤

查看试题解析
13. 某同学在解关于x的方程ax²+bx+c＝0时，只抄对了a＝1，b＝-8，解出其中一个根是x＝-1．他核对时发现所抄的c是原方程的c的相反数，则原方程的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个根是x＝1 D、不存在实数根

查看试题解析
14. 已知在正六边形 $A B C D E F$ 中，G是 $D E$ 的中点，连接 $B G$ 并延长交 $C D$ 的延长线于点H，若 $△ B C H$ 的面积为6，则五边形 $A B G E F$ 的面积为（）

A、12 B、10 C、8 D、6

查看试题解析

二、填空题

15. 用因式分解法解一元二次方程 ${(x - 1)}^{2} - 4 = 0$ 时，要转化成两个一元一次方程求解，其中的一个方程是 $x - 1 + 2 = 0$ ，则另一个方程是，一元二次方程 ${(x - 1)}^{2} - 4 = 0$ 的解是．

查看试题解析
16. 如图为某学校学生年龄分布情况扇形统计图，根据统计图，解决下列问题：

(1)、m=；

(2)、该学校学生的平均年龄为岁．

查看试题解析
17. 如图， $△ A B C$ 是一张直角三角形彩色纸， $∠ A C B = 90 ° ， A C = 30 c m ， B C = 40 c m$ ， $C D ⊥ A B$ 于点D．

① $C D =$ $c m$ ；
②将斜边上的高 $C D$ 进行五等分，然后裁出4张宽度相等的长方形纸条．则这4张纸条的面积和是 $c m^{2}$ ．

查看试题解析

三、解答题

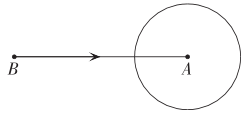
18. 如图，某海域以点A为圆心、 $3 k m$ 为半径的圆形区域为多暗礁的危险区，但渔业资源丰富，渔船要从点B处前往A处进行捕鱼，B、A两点之间的距离是 $10 k m$ ，如果渔船始终保持 $10 k m / h$ 的航速行驶，那么在什么时段内，渔船是安全的？渔船何时进入危险区域？

查看试题解析
19. 如图， $A D$ 是 $△ A B C$ 的高，若 $A D = 6$ ， $t a n C = \frac{3}{2}$ ， $B C = 12$ ．

(1)、求 $C D$ 边的长；

(2)、求 $c o s B$ 的值．

查看试题解析
20. 数轴上，A、B、C分别表示数为-3、5、7．

(1)、求这个三个数的平均数；

(2)、添加一个点D，若这四个点的表示的数组成一组数据，且这组数据唯一的众数与中位数相等，求点D表示的数．

查看试题解析
21. 规定：在平面直角坐标系中，横坐标与纵坐标均为整数的点，叫做整点，点 $A (2 ， 2)$ ， $B (m ， 1)$ 在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上；

(1)、m=；

(2)、已知 $b > 0$ ，过点 $C (- 4 b ， 0)$ 、D点 $(0 ， b)$ 作直线交双曲线 $y = \frac{k}{x} (x > 0)$ 于E点，连接OB，若阴影区域（不包括边界）内有4个整点，求b的取值范围．

查看试题解析
22. 水果店老板以每斤2元的价格购进苹果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，每斤苹果的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出280斤，老板决定降价销售．

(1)、若每斤售价降低0.5元，则每天的销售量是斤．

(2)、若每斤售价降低x元，则每天的销售量是斤（用含x的代数式表示，需要化简）；

(3)、水果店老板要想通过销售苹果每天盈利300元，需将每斤苹果的售价定为多少元？

查看试题解析
23. 如图1，在 $△ A B C$ 中， $∠ A = 90 °$ ， $A B = 3$ ， $A C = 4$ ，点M是边 $A B$ 上的动点（不与A、B重合）， $M Q ⊥ B C$ 于点Q， $M N ∥ B C$ ，交 $A C$ 于点N，连接 $N Q$ ．

(1)、求证： $△ Q B M ∽ △ A M N$ ；

(2)、若点M为 $A B$ 的中点（如图2），求 $Q B$ 的长；

(3)、若四边形 $B M N Q$ 为平行四边形（如图3），求 $Q B$ 的长．

查看试题解析
24. 如图1所示，在矩形 $O A B C$ 中， $O A = \sqrt{2}$ ， $O C = 1$ ，点D是射线 $O A$ 上一动点，以 $O D$ 为半径作 $⊙ O$ ．

(1)、连接 $C D$ 交 $⊙ O$ 于点E，连接 $O B$ ，当 $D E$ 的中点在 $O B$ 上时，求 $O D$ 的长；

(2)、如图2所示，当 $⊙ O$ 与 $A B$ 边相切时，设 $⊙ O$ 与 $B C$ 交于点F，求劣弧 $\overset{⌢}{A F}$ 的长；

(3)、连接 $A C$ ，若 $⊙ O$ 与 $△ A B C$ 两条边同时相交，请直接写出 $t a n ∠ B C D$ 的取值范围．

查看试题解析

	甲	乙	丙	丁
平均数（分）	$a$	80	90	80
方差	$b$	2.2	5.4	2.4