北京市密云区2022一2023学年九年级上学期期末考试数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
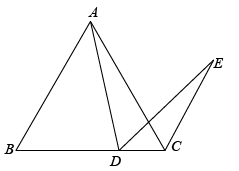
1. 将抛物线向右平移一个单位,得到的新抛物线的表达式是( )A、 B、 C、 D、2. 已知为锐角, , 则的大小是( )A、 B、 C、 D、3. 已知的半径为2,点O到直线l的距离是4,则直线l与的位置关系是( )A、相离 B、相切 C、相交 D、以上情况都有可能4. 如图,中,D、E分别在上, , 则的值为( )
 A、 B、 C、 D、5. 是函数图象上两点,且 , 则的大小关系是( )A、 B、 C、 D、大小不确定6. 已知二次函数 , 则下列说法正确的是( )A、二次函数图象开口向上 B、当时,函数有最大值是3 C、当时,函数有最小值是3 D、当时,y随x增大而增大7. 如图,是的直径,C、D是上两点, , 则的度数是( )
A、 B、 C、 D、5. 是函数图象上两点,且 , 则的大小关系是( )A、 B、 C、 D、大小不确定6. 已知二次函数 , 则下列说法正确的是( )A、二次函数图象开口向上 B、当时,函数有最大值是3 C、当时,函数有最小值是3 D、当时,y随x增大而增大7. 如图,是的直径,C、D是上两点, , 则的度数是( ) A、 B、 C、 D、8. 如图,多边形是的内接正n边形,已知的半径为r,的度数为 , 点O到的距离为d,的面积为S.下面三个推断中.
A、 B、 C、 D、8. 如图,多边形是的内接正n边形,已知的半径为r,的度数为 , 点O到的距离为d,的面积为S.下面三个推断中.
①当n变化时,随n的变化而变化,与n满足的函数关系是反比例函数关系;②若为定值,当r变化时,d随r的变化而变化,d与r满足的函数关系是正比例函数关系;③若n为定值,当r变化时,S随r的变化而变化,S与r满足的函数关系是二次函数关系.其中正确的是( )
A、①② B、①③ C、②③ D、①②③二、填空题
-
9. 在平面直角坐标系中,二次函数图象开口向上,且对称轴是直线x=2,任写出一个满足条件的二次函数的表达式: .10. 已知扇形的圆心角是 , 半径是 , 则扇形的弧长为cm.11. 已知反比例函数的图象位于第二、四象限,则的取值范围为 .12. 在中, , 则的值为 .13. 已知抛物线上部分点的横坐标x和纵坐标y的几组数据如下:
x
-1
1
3
y
2
-2
2
点是抛物线上不同的两点,则 .
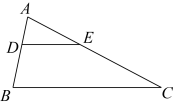
14. 如图,A,B、C三点都在上, , 过点A作的切线与的延长线交于点P,则的度数是 . 15. 如图,矩形中, , E是上一点,与交于点F.则的长为 .
15. 如图,矩形中, , E是上一点,与交于点F.则的长为 .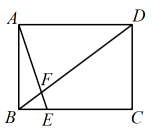 16. 如图,的弦长为2,是的直径, .
16. 如图,的弦长为2,是的直径, .
①的半径长为 .
②P是上的动点,则的最小值是 .
三、解答题
-
17. 计算: .18. 中, , D是边上一点,延长至E,连接 , .
 (1)、求证:;(2)、若 , 求长.19. 中, , 垂足为D, , 求长.
(1)、求证:;(2)、若 , 求长.19. 中, , 垂足为D, , 求长.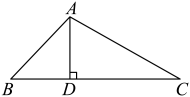 20. 已知二次函数 .(1)、求二次函数图象的顶点坐标及函数图象与x轴的交点坐标;(2)、画出二次函数的示意图,结合图象直接写出当函数值时,自变量x的取值范围.21. 2022年11月29日,搭载神舟十五号载人飞船的运载火箭在酒泉卫星发射中心成功发射.运载火箭从发射点O处发射,当火箭到达A处时、在地面雷达站C处测得点A的仰角为 , 在地面雷达站B处测得点A的仰角为 . 已知 , O、B、C三点在同一条直线上,求B、C两个雷达站之间的距离(结果精确到 , 参考数据).
20. 已知二次函数 .(1)、求二次函数图象的顶点坐标及函数图象与x轴的交点坐标;(2)、画出二次函数的示意图,结合图象直接写出当函数值时,自变量x的取值范围.21. 2022年11月29日,搭载神舟十五号载人飞船的运载火箭在酒泉卫星发射中心成功发射.运载火箭从发射点O处发射,当火箭到达A处时、在地面雷达站C处测得点A的仰角为 , 在地面雷达站B处测得点A的仰角为 . 已知 , O、B、C三点在同一条直线上,求B、C两个雷达站之间的距离(结果精确到 , 参考数据). 22. 如图,内接于 , 是的直径, , 垂足为D.
22. 如图,内接于 , 是的直径, , 垂足为D.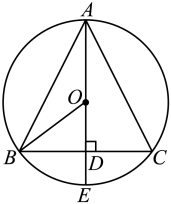 (1)、求证:;(2)、已知的半径为5, , 求长.23. 已知函数的图象上有两点 .(1)、求m,n的值.(2)、已知直线与直线平行,且直线与线段总有公共点,直接写出k值及b的取值范围.24. 如图,是的直径,是的弦,与交于点E, , 延长至F,连接 , 使得 .
(1)、求证:;(2)、已知的半径为5, , 求长.23. 已知函数的图象上有两点 .(1)、求m,n的值.(2)、已知直线与直线平行,且直线与线段总有公共点,直接写出k值及b的取值范围.24. 如图,是的直径,是的弦,与交于点E, , 延长至F,连接 , 使得 . (1)、求证:是的切线;(2)、已知 , , 求的半径长.25. 实心球是北京市初中体育学业水平现场考试选考项目之一.某同学作了2次实心球训练.第一次训练中实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图所示,掷出时起点处高度为 , 当水平距离为时,实心球行进至最高点处.
(1)、求证:是的切线;(2)、已知 , , 求的半径长.25. 实心球是北京市初中体育学业水平现场考试选考项目之一.某同学作了2次实心球训练.第一次训练中实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图所示,掷出时起点处高度为 , 当水平距离为时,实心球行进至最高点处. (1)、求y关于x的函数表达式;(2)、该同学第二次训练实心球的竖直高度y与水平距离x近似满足函数关系: , 记第一次实心球从起点到落地点的水平距离为 , 第二次实心球从起点到落地点的水平距离为 , 则 . (填“>”“=”或“<”).26. 已知抛物线 .(1)、若抛物线经过点 , 求抛物线的对称轴;(2)、已知抛物线上有四个点 , 且 . 比较的大小,并说明理由.
(1)、求y关于x的函数表达式;(2)、该同学第二次训练实心球的竖直高度y与水平距离x近似满足函数关系: , 记第一次实心球从起点到落地点的水平距离为 , 第二次实心球从起点到落地点的水平距离为 , 则 . (填“>”“=”或“<”).26. 已知抛物线 .(1)、若抛物线经过点 , 求抛物线的对称轴;(2)、已知抛物线上有四个点 , 且 . 比较的大小,并说明理由.