北京市门头沟区2022-2023学年九年级上学期期末数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 如果 , 那么的值是( )A、 B、 C、 D、2. 已知⊙O的半径为4,点P在⊙O内,则OP的长可能是( )A、3 B、4 C、5 D、63. 如图,在Rt△ABC中,∠C=90°, AC=3,BC=4,则sinA的值为( )
 A、 B、 C、 D、4. 如果将抛物线向上平移3个单位长度,得到新的抛物线的表达式是( )A、 B、 C、 D、5. 如图, , 相交于点O,且 . 如果 , , 那么的值是( )
A、 B、 C、 D、4. 如果将抛物线向上平移3个单位长度,得到新的抛物线的表达式是( )A、 B、 C、 D、5. 如图, , 相交于点O,且 . 如果 , , 那么的值是( ) A、3 B、4 C、5 D、66. 如图,线段是的直径,如果 , 那么的度数是( )
A、3 B、4 C、5 D、66. 如图,线段是的直径,如果 , 那么的度数是( )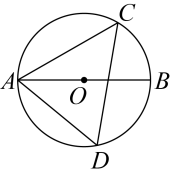 A、 B、 C、 D、7. 二次函数的图象如图所示,那么下列结论正确的是( )
A、 B、 C、 D、7. 二次函数的图象如图所示,那么下列结论正确的是( )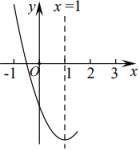 A、 B、 C、 D、一元二次方程的近似解为 ,8. 下面的四个选项中都有两个变量,其中变量y与变量x之间的函数关系可以用如图所示的图像表示的是( )
A、 B、 C、 D、一元二次方程的近似解为 ,8. 下面的四个选项中都有两个变量,其中变量y与变量x之间的函数关系可以用如图所示的图像表示的是( )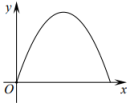 A、圆的面积y与它的半径x; B、正方形的周长y与它的边长x; C、用长度一定的铁丝围成一个矩形,矩形的面积y与一边长x; D、小明从家骑车去学校,路程一定时,匀速骑行中所用时间y与平均速度x;
A、圆的面积y与它的半径x; B、正方形的周长y与它的边长x; C、用长度一定的铁丝围成一个矩形,矩形的面积y与一边长x; D、小明从家骑车去学校,路程一定时,匀速骑行中所用时间y与平均速度x;二、填空题
-
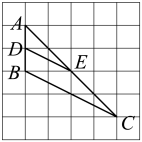
9. 如果 , 那么锐角度.10. 如果一个扇形的圆心角为 , 半径为2,那么该扇形的面积为(结果保留π).11. 在平面直角坐标系中,反比例函数的图象经过点 , , 那么与的大小关系是(填“”,“”或“”)时.12. 如图所示的网格是正方形网格,A,B,C,D,E是网格线的交点,那么的面积与的面积的比是 .
 13. 写出一个二次函数,其图像满足:①开口向下;②当时,y随x的增大而增大.这个二次函数的表达式可以是 .14. 《孙子算经》是中国古代重要的数学著作,其中有首歌谣:“今有竿不知其长,量得影长一百五十寸,立一标杆,长一十五寸,影长五寸,问竿长几何?”.其意思是:“如图,有一根竹竿不知道有多长,量出它在太阳下的影子长150寸,同时立一根15寸的小标杆 , 它的影子长5寸,则竹竿的长为多少?”.答:竹竿的长为寸.
13. 写出一个二次函数,其图像满足:①开口向下;②当时,y随x的增大而增大.这个二次函数的表达式可以是 .14. 《孙子算经》是中国古代重要的数学著作,其中有首歌谣:“今有竿不知其长,量得影长一百五十寸,立一标杆,长一十五寸,影长五寸,问竿长几何?”.其意思是:“如图,有一根竹竿不知道有多长,量出它在太阳下的影子长150寸,同时立一根15寸的小标杆 , 它的影子长5寸,则竹竿的长为多少?”.答:竹竿的长为寸.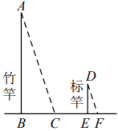 15. 石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知某公园石拱桥的跨度米,拱高米,那么桥拱所在圆的半径米.
15. 石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知某公园石拱桥的跨度米,拱高米,那么桥拱所在圆的半径米. 16. 如图1,在等边中,D是中点,点P为边上一动点,设 , , 如果y与x的函数关系的图象如图2所示,那么 .
16. 如图1,在等边中,D是中点,点P为边上一动点,设 , , 如果y与x的函数关系的图象如图2所示,那么 . 17. 如图,在中,点D在上,连接 . 请添加一个条件 , 使得 , 然后再加以证明.
17. 如图,在中,点D在上,连接 . 请添加一个条件 , 使得 , 然后再加以证明.
三、解答题
-
18. 计算: .19. 下面是小李设计的“作圆的内接等边三角形”的尺规作图过程.
已知:如图1, .

求作:等边 , 使得等边内接于 .
作法:
①如图2,作半径;
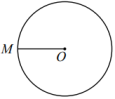
②以M为圆心,长为半径作弧,交于点A,B,连接;
③以B为圆心,长为半径作弧,交于点C;
④连接 , .
∴就是所求作的等边三角形.
根据上述尺规作图的过程,回答以下问题:
(1)、使用直尺和圆规,依作法补全图2(保留作图痕迹);(2)、完成下面的证明.证明:连接 , , , .
由作图可知 ,
∴ , 是等边三角形.
∴ ▲ .
∴ .
∵ ,
∴ . ( )(填推理的依据)
∵ ,
∴是等边三角形.
20. 已知二次函数 (1)、求此二次函数图象的顶点坐标;(2)、求此二次函数图象与x轴的交点坐标;(3)、当时,直接写出x的取值范围.21. 如图,在中, , 点D在上, , 过点B作 , 交的延长线于点E.
(1)、求此二次函数图象的顶点坐标;(2)、求此二次函数图象与x轴的交点坐标;(3)、当时,直接写出x的取值范围.21. 如图,在中, , 点D在上, , 过点B作 , 交的延长线于点E. (1)、求证:;(2)、如果 , , 求的长.22. 在平面直角坐标系xOy中,一次函数的图象与反比例函数的图象的一个交点为 .
(1)、求证:;(2)、如果 , , 求的长.22. 在平面直角坐标系xOy中,一次函数的图象与反比例函数的图象的一个交点为 . (1)、求反比例函数的解析式;(2)、当时,对于x的每一个值,一次函数的值大于反比例函数的值,直接写出k的取值范围.23. 定都阁位于门头沟潭柘寺镇的定都峰上,与通州大运河遥相呼应,形成“东有大运河,西有定都阁”的一道新景观.为测得定都阁的高度,某校数学社团登上定都峰开展实践活动.他们利用无人机在点P处测得定都阁顶端A的俯角α为 , 定都阁底端B的俯角β为 , 此时无人机到地面的垂直距离为米,求定都阁的高 . (结果保留根号)
(1)、求反比例函数的解析式;(2)、当时,对于x的每一个值,一次函数的值大于反比例函数的值,直接写出k的取值范围.23. 定都阁位于门头沟潭柘寺镇的定都峰上,与通州大运河遥相呼应,形成“东有大运河,西有定都阁”的一道新景观.为测得定都阁的高度,某校数学社团登上定都峰开展实践活动.他们利用无人机在点P处测得定都阁顶端A的俯角α为 , 定都阁底端B的俯角β为 , 此时无人机到地面的垂直距离为米,求定都阁的高 . (结果保留根号)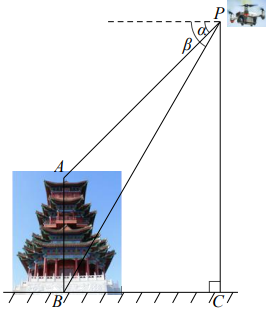 24. 某公园有一个小型喷泉,水柱从垂直于地面的喷水枪喷出,水柱落于地面的路径形状可以看作是抛物线的一部分.记喷出的水柱距喷水枪的水平距离为(单x位:m),距地面的垂直高度为y(单位:m),现测得x与y的几组对应数据如下:
24. 某公园有一个小型喷泉,水柱从垂直于地面的喷水枪喷出,水柱落于地面的路径形状可以看作是抛物线的一部分.记喷出的水柱距喷水枪的水平距离为(单x位:m),距地面的垂直高度为y(单位:m),现测得x与y的几组对应数据如下:水平距离x/m
0
1
2
3
4
5
6
…
垂直高度y/m
0.7
1.6
2.3
2.8
3.1
3.2
3.1
…

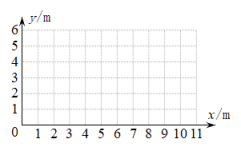
请根据测得的数据,解决以下问题:
(1)、在平面直角坐标系中,描出以表中各组对应数据为坐标的点,并画出该函数的图象;(2)、结合表中所给数据或所画图象,得出水柱最高点距离地面的垂直高度为m;(3)、求所画图象对应的二次函数表达式;(4)、公园准备在水柱下方的地面上竖直安装一根高的石柱,使该喷水枪喷出的水柱恰好经过石柱顶端,则石柱距喷水枪的水平距离为m.(注:不考虑石柱粗细等其他因素)25. 如图,在等腰中, , 以为直径作 , 交于点D,过点D作 , 垂足为E.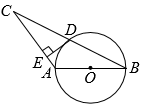 (1)、求证:是的切线;(2)、如果 , , 求的长.26. 在平面直角坐标系中,点 , 在抛物线上,其中 , 设抛物线的对称轴为 .
(1)、求证:是的切线;(2)、如果 , , 求的长.26. 在平面直角坐标系中,点 , 在抛物线上,其中 , 设抛物线的对称轴为 . (1)、当时,如果 , 直接写出 , 的值;(2)、当 , 时,总有 , 求t的取值范围.27. 如图,在中, , 点D在上,连接 , 在直线右侧作 , 且 , 连接交于点F.
(1)、当时,如果 , 直接写出 , 的值;(2)、当 , 时,总有 , 求t的取值范围.27. 如图,在中, , 点D在上,连接 , 在直线右侧作 , 且 , 连接交于点F. (1)、如图1,当时,
(1)、如图1,当时,①依题意补全图1,猜想与之间的数量关系,并证明;
②用等式表示线段 , 的数量关系,并证明.
(2)、如图2,当时,直接用含m的等式表示线段 , 的数量关系.28. 在平面直角坐标系中,对于点 , 给出如下定义:当点 , 满足时,称点N是点M的等积点.已知点 . (1)、在 , , 中,点M的等积点是;(2)、如果点M的等积点N在双曲线上,求点N的坐标;(3)、已知点 , , 的半径为1,连接 , 点A在线段上.如果在上存在点A的等积点,直接写出a的取值范围.
(1)、在 , , 中,点M的等积点是;(2)、如果点M的等积点N在双曲线上,求点N的坐标;(3)、已知点 , , 的半径为1,连接 , 点A在线段上.如果在上存在点A的等积点,直接写出a的取值范围.