北京市海淀区2022-2023学年九年级上学期数学期末试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 刺绣是中国民间传统手工艺之一.下列刺绣图案中,是中心对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 点 关于原点对称的点的坐标是( )A、 B、 C、 D、3. 二次函数的图象向左平移1个单位长度,得到的二次函数解析式为( )A、 B、 C、 D、4. 如图,已知正方形 , 以点为圆心,长为半径作 , 点与的位置关系为( )
2. 点 关于原点对称的点的坐标是( )A、 B、 C、 D、3. 二次函数的图象向左平移1个单位长度,得到的二次函数解析式为( )A、 B、 C、 D、4. 如图,已知正方形 , 以点为圆心,长为半径作 , 点与的位置关系为( )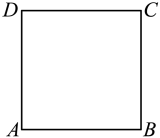 A、点在外 B、点在内 C、点在上 D、无法确定5. 若点 , 在抛物线上,则的值为( )A、2 B、1 C、0 D、-16. 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该角度可以为( )
A、点在外 B、点在内 C、点在上 D、无法确定5. 若点 , 在抛物线上,则的值为( )A、2 B、1 C、0 D、-16. 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该角度可以为( ) A、 B、 C、 D、7. 如图,过点作的切线 , , 切点分别是 , , 连接 . 过上一点作的切线,交 , 于点 , . 若 , 的周长为4,则的长为( )
A、 B、 C、 D、7. 如图,过点作的切线 , , 切点分别是 , , 连接 . 过上一点作的切线,交 , 于点 , . 若 , 的周长为4,则的长为( )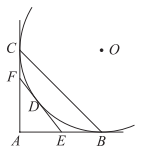 A、2 B、 C、4 D、8. 遥控电动跑车竞速是青少年喜欢的活动.如图是某赛道的部分通行路线示意图,某赛车从人口A驶入,行至每个岔路口选择前方两条线路的可能性相同,则该赛车从口驶出的概率是( )
A、2 B、 C、4 D、8. 遥控电动跑车竞速是青少年喜欢的活动.如图是某赛道的部分通行路线示意图,某赛车从人口A驶入,行至每个岔路口选择前方两条线路的可能性相同,则该赛车从口驶出的概率是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 二次函数的图象与轴的交点坐标为 .10. 半径为3且圆心角为的扇形的面积为.11. 下表记录了一名球员在罚球线上投篮的结果.
投篮次数
50
100
150
200
300
400
500
投中次数
28
49
78
102
153
208
255
投中频率
0.56
0.49
0.52
0.51
0.51
0.52
0.51
根据以上数据,估计这名球员在罚球线上投篮一次,投中的概率为 .
12. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是 .13. 二次函数的图象如图所示,则ab0(填“”,“”或“”). 14. 如图,是的内接三角形,于点 , 若的半径为 , , 则 .
14. 如图,是的内接三角形,于点 , 若的半径为 , , 则 . 15. 对于二次函数 , 与的部分对应值如表所示.在某一范围内,随的增大而减小,写出一个符合条件的的取值范围 .
15. 对于二次函数 , 与的部分对应值如表所示.在某一范围内,随的增大而减小,写出一个符合条件的的取值范围 .…
-1
0
1
2
3
…
…
-3
1
3
3
1
…
16. 如图, , , 分别是某圆内接正六边形、正方形、等边三角形的一边.若 , 下面四个结论中,①该圆的半径为2; ②的长为;
③平分; ④连接 , , 则与的面积比为 .
所有正确结论的序号是 .

三、解答题
-
17. 解方程: .18. 已知抛物线过点和 , 求该抛物线的解析式.19. 已知为方程的一个根,求代数式的值.20. 如图,四边形内接于 , 为直径, . 若 , 求的度数.
 21. 为了发展学生的兴趣爱好,学校利用课后服务时间开展了丰富的社团活动.小明和小天参加的篮球社共有甲、乙、丙三个训练场.活动时,每个学生用抽签的方式从三个训练场中随机抽取一个场地进行训练.(1)、小明抽到甲训练场的概率为;(2)、用列表或画树状图的方法,求小明和小天在某次活动中抽到同一场地训练的概率.22. 已知:如图,是的切线,为切点.
21. 为了发展学生的兴趣爱好,学校利用课后服务时间开展了丰富的社团活动.小明和小天参加的篮球社共有甲、乙、丙三个训练场.活动时,每个学生用抽签的方式从三个训练场中随机抽取一个场地进行训练.(1)、小明抽到甲训练场的概率为;(2)、用列表或画树状图的方法,求小明和小天在某次活动中抽到同一场地训练的概率.22. 已知:如图,是的切线,为切点.求作:的另一条切线 , 为切点.
作法:以为圆心,长为半径画弧,交于点;
作直线 .
直线即为所求.
 (1)、根据上面的作法,补全图形(保留作图痕迹);(2)、完成下面证明过程.
(1)、根据上面的作法,补全图形(保留作图痕迹);(2)、完成下面证明过程.证明:连接 , , .
∵是的切线,为切点,
∴ .
∴ .
在与中,
∴ . ∴ .
∴于点 . ∵是的半径,
∴是的切线( )(填推理的依据).
23. 紫砂壶是我国特有的手工制造陶土工艺品,其制作过程需要几十种不同的工具,其中有一种工具名为“带刻度嘴巴架”,其形状及使用方法如图1。当制显艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时,就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上.图2是符合题意使用该工具时的示意图.如图3,为某紫砂壶的壶口,已知 , 两点在上,直线过点 , 且于点 , 交于点 . 若 , , 求这个紫砂壶的壶口半径的长.
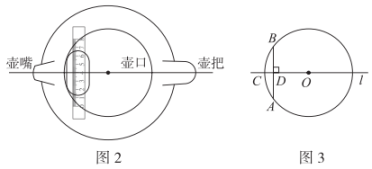 24. 如图,是的直径,点在上.过点作的切线 , 过点作于点 .
24. 如图,是的直径,点在上.过点作的切线 , 过点作于点 . (1)、求证:平分;(2)、连接 , 若 , , 求的长.25. 学校举办“科技之星”颁奖典礼,颁奖现场人口为一个拱门.小明要在拱门上顺次粘贴“科”“技”“之”“星”四个大字(如图1),其中,“科”与“星”距地面的高度相同,“技”与“之”距地面的高度相同,他发现拱门可以看作是抛物线的一部分,四个字和五角星可以看作抛物线上的点.通过测量得到拱门的最大跨度是10米,最高点的五角星距地面6.25米.
(1)、求证:平分;(2)、连接 , 若 , , 求的长.25. 学校举办“科技之星”颁奖典礼,颁奖现场人口为一个拱门.小明要在拱门上顺次粘贴“科”“技”“之”“星”四个大字(如图1),其中,“科”与“星”距地面的高度相同,“技”与“之”距地面的高度相同,他发现拱门可以看作是抛物线的一部分,四个字和五角星可以看作抛物线上的点.通过测量得到拱门的最大跨度是10米,最高点的五角星距地面6.25米. (1)、请在图2中建立平面直角坐标系 , 并求出该抛物线的解析式;(2)、“技”与“之”的水平距离为米.小明想同时达到如下两个设计效果:
(1)、请在图2中建立平面直角坐标系 , 并求出该抛物线的解析式;(2)、“技”与“之”的水平距离为米.小明想同时达到如下两个设计效果:① “科”与“星”的水平距离是“技”与“之”的水平距离的2倍;
②“技”与“科”距地面的高度差为1.5米.
小明的设计能否实现?若能实现,直接写出的值;若不能实现,请说明理由.
26. 在平面直角坐标系中,抛物线过点 . (1)、求(用含的式子表示);(2)、抛物线过点 , , .
(1)、求(用含的式子表示);(2)、抛物线过点 , , .①判断: ▲ 0(填“>”“<”或“=”);
②若 , , 恰有两个点在轴上方,求的取值范围.