安徽省亳州市2022--2023学年九年级上学期期末数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列各式中,y是x的二次函数的是( )A、 B、 C、 D、2. 已知2x=3y(xy≠0),那么下列比例式中成立的是( )A、 B、 C、 D、3. 在 △ 中,∠ ,如果 , ,那么cosA的值为( )
 A、 B、 C、 D、4. 如果反比例函数 (a是常数)的图象在第一、三象限,那么a的取值范围是( )A、a<0 B、a>0 C、a<2 D、a>25. 下列说法中,真命题的个数是( )
A、 B、 C、 D、4. 如果反比例函数 (a是常数)的图象在第一、三象限,那么a的取值范围是( )A、a<0 B、a>0 C、a<2 D、a>25. 下列说法中,真命题的个数是( )①任何三角形有且只有一个外接圆;②任何圆有且只有一个内接三角形;③三角形的外心不一定在三角形内;④三角形的外心到三角形三边的距离相等;⑤经过三点确定一个圆;
A、1 B、2 C、3 D、46. 若抛物线y=﹣x2+bx+c经过点(﹣2,3),则2c﹣4b﹣9的值是( )
A、5 B、﹣1 C、4 D、187. 如图,直线a∥b∥c,则下列结论错误的为( ) A、 B、 C、 D、8. 在△ABC中,∠C=90°,sinA= , 则cosB的值为( )
A、 B、 C、 D、8. 在△ABC中,∠C=90°,sinA= , 则cosB的值为( )
A、1 B、 C、 D、9. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )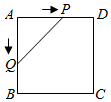 A、
A、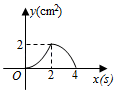 B、
B、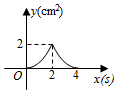 C、
C、 D、
D、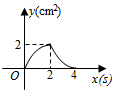 10. 如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
10. 如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )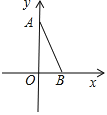 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
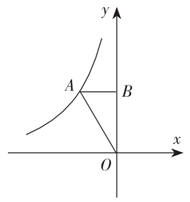
11. 如图,已知A为反比例函数 的图象上一点,过点A作 轴,垂足为B.若 的面积为2,则k的值为 .
 12. 两个相似三角形的面积比为1:9,则它们的周长比为 .13. 若扇形的圆心角为120°的弧长是12πcm,则这个扇形的面积是 cm2 .14. 如图的两条直角边 , , 点D沿从A向B运动,速度是 , 同时,点E沿从B向C运动,速度为 . 动点E到达点C时运动终止.连接 .
12. 两个相似三角形的面积比为1:9,则它们的周长比为 .13. 若扇形的圆心角为120°的弧长是12πcm,则这个扇形的面积是 cm2 .14. 如图的两条直角边 , , 点D沿从A向B运动,速度是 , 同时,点E沿从B向C运动,速度为 . 动点E到达点C时运动终止.连接 . (1)、当动点运动秒时,与相似;(2)、当动点运动秒时, .
(1)、当动点运动秒时,与相似;(2)、当动点运动秒时, .三、解答题
-
15. 计算: .16. 已知抛物线过点和 , 求该抛物线的解析式.17. 在平面直角坐标系中,三个顶点坐标分别是 , , .
 (1)、作出关于O点逆时针旋转得到;(2)、作出以点O为位似中心,位似比为1的 .18. 用“
(1)、作出关于O点逆时针旋转得到;(2)、作出以点O为位似中心,位似比为1的 .18. 用“ ”和“
”和“ ”分别代表甲种植物和乙种植物,为了美化环境,采用如图所示的方案种植:
”分别代表甲种植物和乙种植物,为了美化环境,采用如图所示的方案种植: (1)、观察图形,寻找规律,并将下表填写完整:
(1)、观察图形,寻找规律,并将下表填写完整:图序
①
②
③
④

1
4
9

4
9
(2)、分别表示出第n个图形中甲种植物和乙种植物的株数.19. 已知:如图,为的直径,C为上一点,和过点C的切线互相垂直,垂足为D. (1)、求证:平分 .(2)、过点O作线段的垂线 , 垂足为E.若 , . 求垂线段OE的长.20. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 , 箱长 , 拉杆的长度都相等,在上,在上,支杆 , 请根据以上信息,解决下列问题.
(1)、求证:平分 .(2)、过点O作线段的垂线 , 垂足为E.若 , . 求垂线段OE的长.20. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 , 箱长 , 拉杆的长度都相等,在上,在上,支杆 , 请根据以上信息,解决下列问题. (1)、求的长度(结果保留根号);(2)、求拉杆端点到水平滑杆的距离(结果保留根号).21. 如图,反比例函数的图象与正比例函数的图象交于、B两点.点在反比例函数图象上,连接 , 交y轴于点N.
(1)、求的长度(结果保留根号);(2)、求拉杆端点到水平滑杆的距离(结果保留根号).21. 如图,反比例函数的图象与正比例函数的图象交于、B两点.点在反比例函数图象上,连接 , 交y轴于点N. (1)、求反比例函数的解析式.(2)、求的面积.22. 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D
(1)、求反比例函数的解析式.(2)、求的面积.22. 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D (1)、求二次函数的表达式。
(1)、求二次函数的表达式。
(2)、在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标(3)、有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从 点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.23.(1)、问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.

填空: ①的值为;②∠DBE的度数为.
(2)、类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由.
 (3)、拓展延伸
(3)、拓展延伸如面3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.
