吉林省长春市榆树市2022-2023学年七年级上学期期末数学试题
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. -5的相反数是( )A、5 B、-5 C、 D、-2. 某市在一次扶贫助残活动中,捐款约61800000元,请将61800000元用科学记数法表示,其结果为( )A、6.18×107元 B、6.18×106元 C、0.618×109元 D、618×105元3. 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
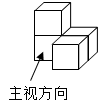 A、
A、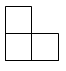 B、
B、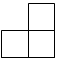 C、
C、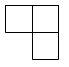 D、
D、 4. 如图,直线b、c被直线a所截,则与是( )
4. 如图,直线b、c被直线a所截,则与是( ) A、对顶角 B、同位角 C、内错角 D、同旁内角5. 多项式﹣5xy+xy2﹣1是( )A、二次三项式 B、三次三项式 C、四次三项式 D、五次三项式6. 如图,将军要从村庄A去村外的河边饮马,有三条路AB、AC、AD可走,将军沿着AB路线到的河边,他这样做的道理是( )
A、对顶角 B、同位角 C、内错角 D、同旁内角5. 多项式﹣5xy+xy2﹣1是( )A、二次三项式 B、三次三项式 C、四次三项式 D、五次三项式6. 如图,将军要从村庄A去村外的河边饮马,有三条路AB、AC、AD可走,将军沿着AB路线到的河边,他这样做的道理是( ) A、两点之间,线段最短 B、两点之间,直线最短 C、两点确定一条直线 D、直线外一点与直线上各点连接的所有线段中,垂线段最短7.
A、两点之间,线段最短 B、两点之间,直线最短 C、两点确定一条直线 D、直线外一点与直线上各点连接的所有线段中,垂线段最短7.如图,AB∥CD , 则图中∠1、∠2、∠3关系一定成立的是( )
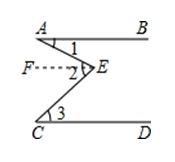 A、∠1+∠2+∠3=180° B、∠1+∠2+∠3=360° C、∠1+∠3=2∠2 D、∠1+∠3=∠2
A、∠1+∠2+∠3=180° B、∠1+∠2+∠3=360° C、∠1+∠3=2∠2 D、∠1+∠3=∠2二、多选题
-
8. 下列代数式符合书写要求的是( )A、ab3 B、1a C、a+4 D、a÷b
三、填空题
-
9. 用“<”号或“>”填空:-30.10. 单项式﹣4ab2的系数是 .11. 把多项式2x﹣1﹣3x2+4x3按x的降幂排列为 .12. 下列三个日常现象:

其中,可以用“两点之间线段最短”来解释的是 (填序号).
13. 已知正方体的一个表面展开图如图所示,则原正方体上“城”的对面的汉字是在 . 14. 某滑雪场在“元旦”期间推出特惠活动:票价每人140元,团体购票超过20人,票价可以享受八折优惠.活动期间,某旅游团有m(m>20)人来该滑雪场游玩,则应付票价总额为 元.
14. 某滑雪场在“元旦”期间推出特惠活动:票价每人140元,团体购票超过20人,票价可以享受八折优惠.活动期间,某旅游团有m(m>20)人来该滑雪场游玩,则应付票价总额为 元.四、解答题
-
15. 计算:(1)、﹣21+16﹣(﹣13).(2)、﹣13﹣6÷(﹣3)×(﹣)2 .16. 计算:(1)、x﹣2x﹣3x+6x.(2)、(3a2﹣a+7)﹣(﹣4a2+2a+6).17. 先化简,再求值: , 其中 , .18. 如图,已知线段AB=24cm,延长AB至C,使得BC=AB,
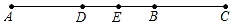 (1)、求AC的长;(2)、若D是AB的中点,E是AC的中点,求DE的长.19. 一块三角尺的形状和尺寸如图所示,直角边的边长为 ,圆孔的半径为 .
(1)、求AC的长;(2)、若D是AB的中点,E是AC的中点,求DE的长.19. 一块三角尺的形状和尺寸如图所示,直角边的边长为 ,圆孔的半径为 . (1)、求阴影部分的面积 ;(2)、当 , 时,求 的值( 取3.14).20. 如图,平面上两点C、D在直线AB的同侧,按下列要求画图并填空.
(1)、求阴影部分的面积 ;(2)、当 , 时,求 的值( 取3.14).20. 如图,平面上两点C、D在直线AB的同侧,按下列要求画图并填空.
( 1 )画直线AC;
( 2 )画射线CD;
( 3 )画线段BD;
( 4 )过点D画垂线段DF⊥AB,垂足为F;
( 5 )点D到直线AB的距离是线段 ▲ 的长.
21. 如图, , , 试说明 . 请完善解答过程,并在括号内填写相应的理论根据.
解:∵(已知),
∴ ▲ ( ).
∵(已知),
∴ ▲ ( ).
∴ ▲ ▲ (平行于同一直线的两直线平行).
∴( ).
22. 莹莹家里今年种植的猕猴桃获得大丰收,她家卖给了一位客户10箱猕猴桃.莹莹帮助爸爸记账,每箱猕猴桃的标准重量为5千克,超过标准重量的部分记为“+”,不足标准重量的部分记为“-”,莹莹的记录如下(单位:千克):+0.15,+0.25,-0.2,+0.1,-0.2,+0.3,-0.2,0,+0.05,-0.15.(1)、计算这10箱猕猴桃的总重量为多少千克?(2)、如果猕猴桃的价格为12元/千克,计算莹莹家出售这10箱猕猴桃共收入多少元?(精确到1元)(3)、若都用这种纸箱装,莹莹家的猕猴桃共能装500箱,按照12元/千克的价格,把猕猴桃全部出售,莹莹家大约能收入多少元?(精确到万位,用科学记数法表示)23. 【感知】已知:如图①,点E在AB上,且CE平分 , . 求证: .(1)、将下列证明过程补充完整: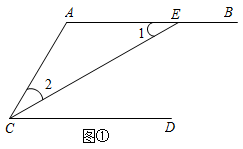
证明:∵CE平分(已知),
∴ ▲ (角平分线的定义),
∵(已知),
∴ ▲ (等量代换),
∴( ).
(2)、【探究】已知:如图②,点E在AB上,且CE平分 , . 求证: . (3)、【应用】如图③,BE平分 , 点A是BD上一点,过点A作交BE于点E, , 直接写出的度数.
(3)、【应用】如图③,BE平分 , 点A是BD上一点,过点A作交BE于点E, , 直接写出的度数. 24. 如图,直线与直线相交于点 , 射线表示正北方向,射线表示正东方向.已知射线的方向是南偏东 , 射线的方向是北偏东 , 且的角与的角互余.
24. 如图,直线与直线相交于点 , 射线表示正北方向,射线表示正东方向.已知射线的方向是南偏东 , 射线的方向是北偏东 , 且的角与的角互余.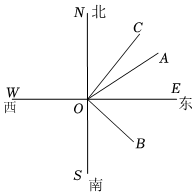 (1)、①若 , 则射线的方向是;
(1)、①若 , 则射线的方向是;②图中与互余的角有 , 与互补的角有 .
(2)、若射线是的平分线,则用含的代数式表示
-