吉林省长春市双阳区2022-2023学年七年级上学期期末数学试题
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 2022年11月21日,卡塔尔世界杯正式拉开帷幕.据估计,此次卡塔尔世界杯花费超220000000000美元,超过了历届世界杯预算的总和,被誉为“最贵的一届世界杯”.将数据220000000000用科学记数法表示为( )A、 B、 C、 D、3. 如图是由7个相同的小正方体组合而成的立体图形,其左视图是( )
 A、
A、 B、
B、 C、
C、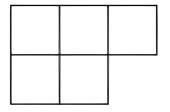 D、
D、 4. 下列代数式符合书写要求的是( )A、 B、 C、 D、5. 单项式的次数是( )A、 B、3 C、5 D、66. 用代数式表示“a的3倍与b的差的平方”,正确的是( )A、3(a﹣b)2 B、(3a﹣b)2 C、3a﹣b2 D、(a﹣3b)27. 如图,直线与直线相交,交点为 , , 平分 , 若则的度数为( )
4. 下列代数式符合书写要求的是( )A、 B、 C、 D、5. 单项式的次数是( )A、 B、3 C、5 D、66. 用代数式表示“a的3倍与b的差的平方”,正确的是( )A、3(a﹣b)2 B、(3a﹣b)2 C、3a﹣b2 D、(a﹣3b)27. 如图,直线与直线相交,交点为 , , 平分 , 若则的度数为( ) A、 B、 C、 D、8. 在算式的“□”内填上下列运算符号,使计算结果最大,这个符号是( )A、+ B、- C、× D、÷9. 已知|a|=8,|b|=3,且|a-b|=b-a,则a+b的值为( )A、5或11 B、-5或-11 C、-5 D、-1110. 如图,已知O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,若OC是 的平分线,则下列结论正确的是( )
A、 B、 C、 D、8. 在算式的“□”内填上下列运算符号,使计算结果最大,这个符号是( )A、+ B、- C、× D、÷9. 已知|a|=8,|b|=3,且|a-b|=b-a,则a+b的值为( )A、5或11 B、-5或-11 C、-5 D、-1110. 如图,已知O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,若OC是 的平分线,则下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 中国人很早就开始使用负数,中国古代数学著作《九章算术》的方程一章,在世界数学史上首次引入负数.下图是小明家长11月份的微信账单,如果收入3377.51元记作元,那么支出5333.73元记作元.
 12. 用四舍五入法,按括号中的要求取近似数: . (精确到百分位)13. 在括号内填入适当的项: .14. 把多项式按的升幂排列为 .15. 如图,在有序号的小正方形中选出一个,它与图中五个有阴影的小正方形组合后,能构成正方体的表面展开图的是 .
12. 用四舍五入法,按括号中的要求取近似数: . (精确到百分位)13. 在括号内填入适当的项: .14. 把多项式按的升幂排列为 .15. 如图,在有序号的小正方形中选出一个,它与图中五个有阴影的小正方形组合后,能构成正方体的表面展开图的是 .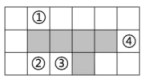 16. 大自然中存在着许多奇妙的现象,科学家通过观察惊奇地发现,植物的茎叶和果实几乎都是按照 , 的模式排列的.这样,植物的茎叶和果实就可以占有最大的空间,以获取最多的阳光,承接最多的雨水.那么的补角是度.17. 代数式 , 则 .18. 探索规律:用黑色棋子按如图的方式摆出正方形,依此规律,第个图案中有个黑色的棋子(用含的代数式表示).
16. 大自然中存在着许多奇妙的现象,科学家通过观察惊奇地发现,植物的茎叶和果实几乎都是按照 , 的模式排列的.这样,植物的茎叶和果实就可以占有最大的空间,以获取最多的阳光,承接最多的雨水.那么的补角是度.17. 代数式 , 则 .18. 探索规律:用黑色棋子按如图的方式摆出正方形,依此规律,第个图案中有个黑色的棋子(用含的代数式表示).
三、解答题
-
19. 计算:20. 计算:21. 先化简,再求值: , 其中 , .22. 如图,线段 , 点为线段上一点, , 点 , 分别为和的中点,求线段的长.
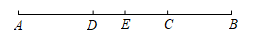 23. 如图,如果 , , 试说明与平行.请完善解答过程,并填空(理由或数学式).
23. 如图,如果 , , 试说明与平行.请完善解答过程,并填空(理由或数学式).
解:∵( )
∴( )(内错角相等,两直线平行.)
∴( )
∵(已知)
∴( )( )
∴( )
24. 疫情期间,出租车司机小王从医院门口出发,在东西方向的道路上免费接送医护人员.如果规定向东为正,向西为负,某天出租车的行程记录如下(单位:千米): , , , , .(1)、医院门口记为0,将最后一名医护人员送到目的地时,小王在医院门口的哪个方向?距离医院多少千米?(2)、若出租车耗油量为升/千米,这天小王共耗油多少升?25. 如图为半圆形计时器,指针绕点从开始逆时针匀速向旋转,速度为10°每秒,指针绕点从开始先顺时针匀速向旋转,到达后立即按原速度逆时针匀速向旋转,速度为20°每秒,两指针同时从起始位置出发,当到达时,两指针都停止旋转.设旋转时间为秒 (1)、当时,度;(2)、度(用含的代数式表示);(3)、当时,与首次重合;(4)、求的度数(用含的代数式表示,并写出相对应的的取值范围);
(1)、当时,度;(2)、度(用含的代数式表示);(3)、当时,与首次重合;(4)、求的度数(用含的代数式表示,并写出相对应的的取值范围);