北京市延庆区2022-2023学年七年级上学期期末考试数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.如果向东走5米记为+5米,则向西走3米记为( )A、+5米 B、﹣5米 C、+3米 D、﹣3米2. 2022年11月6日7点30分,2022北京马拉松鸣枪起跑,起点为天安门广场,终点为奥林匹克森林公园景观大道,全程42.195公里.为了保障赛事竞赛组织工作,组委会选派了5200名志愿者参与工作,将5200用科学记数法表示应为( )A、 B、 C、 D、3. 下面四个立体图形中,从正面去观察它,得到的平面图形是三角形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 若是关于的方程的解,则的值为( )A、2 B、3 C、1 D、6. 有理数 , 在数轴上的对应点的位置如图所示,则正确的结论是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 若是关于的方程的解,则的值为( )A、2 B、3 C、1 D、6. 有理数 , 在数轴上的对应点的位置如图所示,则正确的结论是( )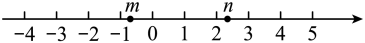 A、 B、 C、 D、7. 如图,点A、B在直线l上,点C是直线l外一点,可知 ,其依据是( )
A、 B、 C、 D、7. 如图,点A、B在直线l上,点C是直线l外一点,可知 ,其依据是( )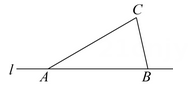 A、两点之间,线段最短 B、两点确定一条直线 C、两点之间,直线最短 D、直线比线段长8. 下列四个图中,能用 , , 三种方法表示同一个角的是( )A、
A、两点之间,线段最短 B、两点确定一条直线 C、两点之间,直线最短 D、直线比线段长8. 下列四个图中,能用 , , 三种方法表示同一个角的是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,点P是直线l外一点,从点P向直线l引PA,PB,PC,PD(点A,B,C,D在直线l上)4条线段,其中于点C.这4条线段中,长度最短的是( )
9. 如图,点P是直线l外一点,从点P向直线l引PA,PB,PC,PD(点A,B,C,D在直线l上)4条线段,其中于点C.这4条线段中,长度最短的是( ) A、PA B、PB C、PC D、PD10. 一个正方体的展开图如图所示,如果正方体相对的两个面所标的数字均互为相反数,那么的值为( )
A、PA B、PB C、PC D、PD10. 一个正方体的展开图如图所示,如果正方体相对的两个面所标的数字均互为相反数,那么的值为( )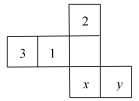 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. -2的绝对值是12. 若代数式﹣5x6y3与2x2ny3是同类项,则常数n的值是.13. 计算: .14. 如图,点在直线上,于点 , 若 , 则的度数为 .
 15. 如图所示的网格是正方形网格,点A,B,C,D,O是网格线交点,那么 (填“>”,“<”或“=”).
15. 如图所示的网格是正方形网格,点A,B,C,D,O是网格线交点,那么 (填“>”,“<”或“=”). 16. 《九章算术》是一部与现代数学的主流思想完全吻合的中国数学经典著作.其中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?意思是:有若干人共同购买某种物品,如果每人出8钱,则多3钱;如果每人出7钱,则少4钱,问共有多少人?物品的价格是多少钱?用一元一次方程的知识解答上述问题设共有x人,依题意,可列方程为 .
16. 《九章算术》是一部与现代数学的主流思想完全吻合的中国数学经典著作.其中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?意思是:有若干人共同购买某种物品,如果每人出8钱,则多3钱;如果每人出7钱,则少4钱,问共有多少人?物品的价格是多少钱?用一元一次方程的知识解答上述问题设共有x人,依题意,可列方程为 .
 17. 点 , , 在同一条直线上,如果 , , 那么 .18. 按一定规律排列的一列数为 , 2, , 8, , 18,…,则第9个数为 , 第个数为 .
17. 点 , , 在同一条直线上,如果 , , 那么 .18. 按一定规律排列的一列数为 , 2, , 8, , 18,…,则第9个数为 , 第个数为 .三、解答题
-
19. 计算:(1)、(2)、20. 计算:(1)、(2)、21. 先化简,再求值: , 其中 , .22. 解方程:(1)、(2)、23. 如图,已知平面上三点 , , , 按下列要求画图,并回答问题:
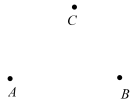 (1)、画射线 , 线段;(2)、连接 , 并在的延长线上取一点 , 使得;(3)、画直线;(4)、通过测量可得,点到直线的距离是 . (精确到)24. 列方程解应用题:某校组织部分师生去北京世园公园参加志愿服务活动.为践行“绿色出行,节能减排”的环保理念,选择骑自行车和步行两种出行方式.已知参加志愿服务活动的教师和学生共30人;其中选择步行人数比选择骑自行车人数的2倍还多3人,问选择骑自行车参加志愿服务活动的共有多少人?25. 如图,点是线段上的点,点是线段的中点, , , 求线段的长.
(1)、画射线 , 线段;(2)、连接 , 并在的延长线上取一点 , 使得;(3)、画直线;(4)、通过测量可得,点到直线的距离是 . (精确到)24. 列方程解应用题:某校组织部分师生去北京世园公园参加志愿服务活动.为践行“绿色出行,节能减排”的环保理念,选择骑自行车和步行两种出行方式.已知参加志愿服务活动的教师和学生共30人;其中选择步行人数比选择骑自行车人数的2倍还多3人,问选择骑自行车参加志愿服务活动的共有多少人?25. 如图,点是线段上的点,点是线段的中点, , , 求线段的长.
请将下面的解题过程补充完整:
解: ▲ ▲ , , ,
▲ .
点是线段的中点,
▲ . (理由: ▲ )
▲ .
26. 阅读材料:学习了一元一次方程的解法后,老师布置了这样一道题,解方程: .
小东同学的解答过程如下:
解方程: .
解: ……第①步
……第②步
……第③步
……第④步
……第⑤步
解决问题:
(1)、解答过程中的第①步依据是;(2)、检验是否为这个方程的解? . (填“是”或“否”)27. 如图,平分 , . (1)、若 , 求的度数.
(1)、若 , 求的度数.请你补全下列解题过程.
平分 ,
▲ (理由: ▲ )
,
▲ .
▲ ▲ , ,
▲ .
(2)、若 , 直接写出的度数.(用含的式子表示)28. 已知数轴上两点 , , 其中表示的数为 , 表示的数为2.给出如下定义:若在数轴上存在一点 , 使得 , 则称点叫做点 , 的“和距离点”.如图,若点表示的数为0,有 , 则称点为点 , 的“5和距离点”. (1)、如果点为点 , 的“和距离点”,且点在数轴上表示的数为 , 那么的值是;(2)、如果点是数轴上点 , 的“6和距离点”,那么点表示的数为;(3)、如果点在数轴上(不与 , 重合),满足 , 且此时点为点 , 的“和距离点”,求的值.
(1)、如果点为点 , 的“和距离点”,且点在数轴上表示的数为 , 那么的值是;(2)、如果点是数轴上点 , 的“6和距离点”,那么点表示的数为;(3)、如果点在数轴上(不与 , 重合),满足 , 且此时点为点 , 的“和距离点”,求的值.