北京市顺义区2022-2023学年七年级上学期期末考试数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列几何体中,是圆锥的为( )A、
 B、
B、 C、
C、 D、
D、 2. 长江干流上的葛洲坝、三峡向家坝、溪洛渡、白鹤滩、乌东德6座巨型梯级水电站,共同构成目前世界上最大的清洁能源走廊,总装机容量71695000千瓦,将71695000用科学记数法表示为( )A、 B、 C、 D、3. 下列四个数中,绝对值最小的数是( )A、-3 B、0 C、1 D、24. 如图,点P在直线外, , , 则线段的值可能为( )
2. 长江干流上的葛洲坝、三峡向家坝、溪洛渡、白鹤滩、乌东德6座巨型梯级水电站,共同构成目前世界上最大的清洁能源走廊,总装机容量71695000千瓦,将71695000用科学记数法表示为( )A、 B、 C、 D、3. 下列四个数中,绝对值最小的数是( )A、-3 B、0 C、1 D、24. 如图,点P在直线外, , , 则线段的值可能为( ) A、1 B、2 C、3 D、45. 下列各式的结果为负数的是( )A、 B、 C、 D、6. 下列变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么7. 在下面的图形中,不是正方体的展开图的是( )A、
A、1 B、2 C、3 D、45. 下列各式的结果为负数的是( )A、 B、 C、 D、6. 下列变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么7. 在下面的图形中,不是正方体的展开图的是( )A、 B、
B、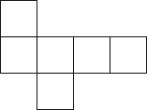 C、
C、 D、
D、 8. 有理数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
8. 有理数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( ) A、 B、 C、 D、9. 下列等式成立的是( )A、 B、 C、 D、10. 如图,大长方形是由5个完全相同的小长方形和一个边长为的正方形拼成,则大长方形的面积是( )
A、 B、 C、 D、9. 下列等式成立的是( )A、 B、 C、 D、10. 如图,大长方形是由5个完全相同的小长方形和一个边长为的正方形拼成,则大长方形的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的倒数是.12. 如果收入10元记作元,那么支出10元记作 .13. 写出一个比-3大的负有理数 .14. 单项式的系数是 , 次数是 .15. 有一个两位数,个位数字是n,十位数字是m,则这个两位数可表示为 .16. 已知关于x的方程的解是 , 则a的值是 .17. 如图,C,D,E是线段上的三点,E为中点, , , , 则 .
 18. 某食品厂从生产的袋装食品中抽出样品10袋,检测每袋的质量是否符合标准,超过或不足的部分用正数或负数来表示,记录如下表:
18. 某食品厂从生产的袋装食品中抽出样品10袋,检测每袋的质量是否符合标准,超过或不足的部分用正数或负数来表示,记录如下表:与标准质量的差值/g
0
1
2
3
袋数
1
3
2
1
2
1
若每袋标准质量为 , 则抽样检测的总质量为 .
19. 如图,这是顺义区第一座互通式立交桥——燕京桥,如果将顺平路和通顺路看做是两条直线,那么这两条直线的位置关系是 .
①相交 ②不相交 ③平行 ④在同一平面内 ⑤不在同一平面内
20. 如图,数轴上有M,N两点和一条线段 , 我们规定:若线段的中点R在线段上(点R能与点P或点Q重合),则称点M与点N关于线段 “中线对称”.
已知点O为数轴的原点,点A表示的数为 , 点B表示的数为4,点C表示的数为x,若点A与点C关于线段 “中线对称”,则x的最大值为 .
三、解答题
-
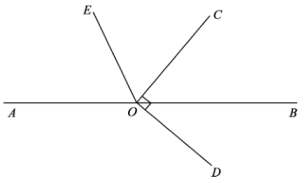
21.22.23.24.25. 已知与是同类项,求代数式的值.26. 解方程:27. 解方程:28. 如图,点O为直线上一点,平分∠AOC, , , 求的度数.
 29. 如图,平面内有三个点A,B,C,按要求完成下列问题:
29. 如图,平面内有三个点A,B,C,按要求完成下列问题: (1)、在图中画出直线 , 射线 , 线段;(2)、观察图形发现,线段 , 得出这个结论的依据是:;(3)、平面内是否存在点D,使得?如果存在,在图中画出一个满足条件的点D;如果不存在,说明理由.30. 列方程解应用题:某中学组织部分师生去北京展览馆参观“奋进新时代”主题成就展.如果单租45座客车若干辆,则全部坐满;如果单租60座的客车,则少租一辆,且余15个座位.求该校前去参观的师生总人数.
(1)、在图中画出直线 , 射线 , 线段;(2)、观察图形发现,线段 , 得出这个结论的依据是:;(3)、平面内是否存在点D,使得?如果存在,在图中画出一个满足条件的点D;如果不存在,说明理由.30. 列方程解应用题:某中学组织部分师生去北京展览馆参观“奋进新时代”主题成就展.如果单租45座客车若干辆,则全部坐满;如果单租60座的客车,则少租一辆,且余15个座位.求该校前去参观的师生总人数.