北京市丰台区2022-2023学年七年级上学期期末数学试卷
试卷更新日期:2023-02-09 类型:期末考试
一、单选题
-
1. 下列几何体中,是圆柱的为( )A、
 B、
B、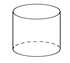 C、
C、 D、
D、 2. 近十年来,我国居民人均可支配收入从16500元增加到35100元.将35100用科学记数法表示应为( )A、 B、 C、 D、3. 下列各组中的两项,属于同类项的是( )A、与 B、与 C、与 D、与4.
2. 近十年来,我国居民人均可支配收入从16500元增加到35100元.将35100用科学记数法表示应为( )A、 B、 C、 D、3. 下列各组中的两项,属于同类项的是( )A、与 B、与 C、与 D、与4.如图所示的几何体是由一些正方体组合而成的立体图形,则这个几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 如果关于x的方程的解是 , 那么m的值是( )A、 B、2 C、4 D、66. 有理数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
5. 如果关于x的方程的解是 , 那么m的值是( )A、 B、2 C、4 D、66. 有理数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )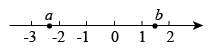 A、 B、 C、 D、7. 如图,点C为线段的中点,点D在线段上,如果 , , 那么线段的长是( )
A、 B、 C、 D、7. 如图,点C为线段的中点,点D在线段上,如果 , , 那么线段的长是( )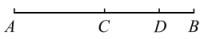 A、2 B、3 C、4 D、58. 我国元朝数学家朱世杰所著的《算学启蒙》中记载了一道问题,大意是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?如果设快马x天可以追上慢马,那么根据题意可列方程为( )A、 B、 C、 D、9. 如图,利用工具测量角,有如下4个结论:
A、2 B、3 C、4 D、58. 我国元朝数学家朱世杰所著的《算学启蒙》中记载了一道问题,大意是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?如果设快马x天可以追上慢马,那么根据题意可列方程为( )A、 B、 C、 D、9. 如图,利用工具测量角,有如下4个结论:①;
②;
③与互为余角;
④与互为补角.
上述结论中,所有正确结论的序号是( )
 A、①②③ B、①② C、③④ D、①③④10. 按下面的运算程序计算:
A、①②③ B、①② C、③④ D、①③④10. 按下面的运算程序计算:
当输入时,输出结果为33;当输入时,输出结果为17.如果输入n的值为正整数 , 输出的结果为25,那么满足条件的n的值最多有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. ﹣3的相反数是 .12. 计算:2ab+3ab= .13. 如图是某几何体的展开图,该几何体是.
 14. 计算: .15. 如图,射线表示的方向是北偏东 , 射线表示的方向是 .
14. 计算: .15. 如图,射线表示的方向是北偏东 , 射线表示的方向是 . 16. 如图是一台冰箱的显示屏,则这台冰箱冷藏室与冷冻室的温差为 .
16. 如图是一台冰箱的显示屏,则这台冰箱冷藏室与冷冻室的温差为 . 17. 用四个如图①所示的长为a,宽为b的长方形,拼成一个如图②所示的图案,得到两个大小不同的正方形,则大正方形的周长是 .
17. 用四个如图①所示的长为a,宽为b的长方形,拼成一个如图②所示的图案,得到两个大小不同的正方形,则大正方形的周长是 . 18. 如图,一个圆上有A,B,C,D,E,F,G七个点.一个小球从点A处出发,沿着圆按逆时针方向移动,移动方式为第k步移动k个点.如:
18. 如图,一个圆上有A,B,C,D,E,F,G七个点.一个小球从点A处出发,沿着圆按逆时针方向移动,移动方式为第k步移动k个点.如:第1步,从点A处移动至点B处;
第2步,从点B处移动至点D处;
第3步,从点D处移动至点G处;
…….
则第5步小球移动至点处;
第100步小球移动至点处.

三、解答题
-
19. 计算: .20. 计算: .21. 解方程: .22. 解方程: .23. 先化简,再求值:
, 其中 , .
24. 如图,平面上有三个点A,B,C.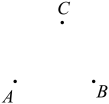 (1)、根据下列语句按要求画图.
(1)、根据下列语句按要求画图.①画直线 , 画射线 , 连接;
②用圆规在线段的延长线上截取 , 连接(保留作图痕迹);
(2)、(填“>”“=”或“<”),依据是 .25. 如图,O是直线上一点,平分 , , . 求的度数.
补充完成下面的解答过程.
解:因为O是直线上一点,
所以 . 因为OC平分 ,
所以 ▲ . 所以与互为余角.
因为 , 所以 ▲ 与 ▲ 互为余角.
所以(依据是: ▲ ).
因为 , 所以 ▲ .
26. 某学校在七年级开展种植类的劳动课程.现需要购买仿生阳光房若干个.经调查发现,同一款式的仿生阳光房在甲、乙两家商店的标价均是100元.新年将至,两家商店开展促销活动,优惠方式如下:
甲商店:每个仿生阳光房按9折(标价的90%)出售;
乙商店:购买的仿生阳光房的个数不超过10时,按标价出售;购买的仿生阳光房的个数超过10时,超过部分按8折(标价的80%)出售.
 (1)、若在甲商店购买10个该款式的仿生阳光房,则花费元;(2)、若在乙商店购买m()个该款式的仿生阳光房,则花费元(用含m的代数式表示);(3)、购买该款式的仿生阳光房的个数为多少时,在甲、乙两家商店的花费相同?27. 有这样一个问题:将一个两位数的十位上的数与个位上的数交换位置,得到一个新数,那么这个新数与原数的和能被11整除吗?
(1)、若在甲商店购买10个该款式的仿生阳光房,则花费元;(2)、若在乙商店购买m()个该款式的仿生阳光房,则花费元(用含m的代数式表示);(3)、购买该款式的仿生阳光房的个数为多少时,在甲、乙两家商店的花费相同?27. 有这样一个问题:将一个两位数的十位上的数与个位上的数交换位置,得到一个新数,那么这个新数与原数的和能被11整除吗?下面是小明的探究过程,请补充完整:
(1)、举例:例① , ;例② , ;例③ .(2)、说理:设一个两位数的十位上的数是a,个位上的数是b,那么这个两位数可表示为 . 依题意得到的新数可表示为 .通过计算说明这个两位数与得到的新数的和能否被11整除: .
(3)、结论:将一个两位数的十位上的数与个位上的数交换位置,得到一个新数,那么这个新数与原数的和(填“能”或“不能”)被11整除.28. 在数轴上,点O表示的数为0,点M表示的数为m().给出如下定义:对于该数轴上的一点P与线段上一点Q,如果线段的长度有最大值,那么称这个最大值为点P与线段的“闭距离”,如图1,若 , 点P表示的数为3,当点Q与点M重合时,线段的长最大,值是4,则点P与线段的“闭距离”为4.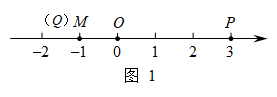 (1)、如图2,在该数轴上,点A表示的数为 , 点B表示的数为2.
(1)、如图2,在该数轴上,点A表示的数为 , 点B表示的数为2.①当时,点A与线段的“闭距离”为 ▲ ;
②若点B与线段的“闭距离”为3,求m的值;
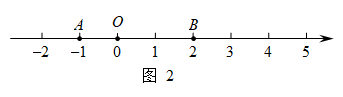 (2)、在该数轴上,点C表示的数为 , 点D表示的数为 , 若线段上存在点G,使得点G与线段的“闭距离”为4,直接写出m的最大值与最小值.
(2)、在该数轴上,点C表示的数为 , 点D表示的数为 , 若线段上存在点G,使得点G与线段的“闭距离”为4,直接写出m的最大值与最小值.