安徽省宣城市宣州区2022~2023学年七年级上学期期末数学试卷

试卷更新日期：2023-02-09 类型：期末考试

进入出卷网下载

一、单选题

1. $2022$ 年国庆假日七天里，民航提供的运力满足了旅客出行需求，中国民航共保障国内外航班 $77800$ 余班，将 $77800$ 用科学记数法表示应为（）

A、 $ 0.778 \times 1 0^{5}$ B、 $ 7.78 \times 1 0^{5}$ C、 $ 7.78 \times 1 0^{4}$ D、 $ 77.8 \times 1 0^{3}$

查看试题解析
2. 如图，A，B两点在数轴上表示的数分别是a，b，下列式子成立的是（）

A、 $a b > 0$ B、 $a + b > 0$ C、 $(a - 1) (b - 1) > 0$ D、 $(a + 1) (b - 1) > 0$

查看试题解析
3. 下列运算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 ${(x + y)}^{2} = x^{2} + y^{2}$ C、 ${(2 x y^{2})}^{3} = 6 x^{3} y^{6}$ D、 $- (x - y) = - x + y$

查看试题解析
4. 若一个多项式减去 $ a^{2} - 3 b^{2}$ 等于 $ a^{2} + 2 b^{2}$ ，则这个多项式是（）

A、 $ - 2 a^{2} + b^{2}$ B、 $ 2 a^{2} - b^{2}$ C、 $ a^{2} - 2 b^{2}$ D、 $ - 2 a^{2} - b^{2}$

查看试题解析
5. 下列说法中，正确的是（　　）

A、若a=b，则 $\frac{a}{c} = \frac{b}{d}$ B、若a=b，则ac=bd C、若a=b，则ac=bc D、若ac=bc，则a=b

查看试题解析
6. 下列说法正确的是（）

A、等角的补角相等 B、相等的角是对顶角 C、和为 $180 °$ 的两角互余 D、内错角互补，两直线平行

查看试题解析
7. 如果 $∠ 1$ 与 $∠ 2$ 互补， $∠ 2$ 与 $∠ 3$ 互余，则 $∠ 1$ 与 $∠ 3$ 的关系是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 1 = 180^{\circ} - ∠ 3$ C、 $∠ 1 = 90^{\circ} + ∠ 3$ D、以上都不对

查看试题解析
8. 下列调查中，适宜采用全面调查方式的是（）

A、调查初三某班体育模拟考试成绩的满分率 B、调查某类烟花爆竹燃放安全情况 C、调查某品牌牛奶的质量合格情况 D、调查全国中学生对“雾霾”的了解情况

查看试题解析
9. 下列说法正确的是（）

A、要了解人们对“低碳生活”的了解程度，宜采用普查方式 B、一组数据5，5，6，7的众数和中位数都是5 C、必然事件发生的概率为100% D、若甲组数据的方差是3.4，乙组数据的方差是1.68，则甲组数据比乙组数据稳定

查看试题解析
10. 用“●”“■”“▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，若要使第三架天平也平衡，那么“？”处应放“■”的个数为（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

11. 在数轴上与 $- 2$ 所对应的点相距4个单位长度的点表示的数是．

查看试题解析
12. 若关于a，b的多项式 $5 (a^{2} - 2 a b + b^{2}) - (a^{2} + m a b - b^{2})$ 中不含有 $a b$ 项，则m= ．

查看试题解析
13. 若 $ 2 x^{5} y^{2 m + 3 n}$ 与 $ - 3 x^{3 m + 2 n} y^{6}$ 是同类项，则 $| m - n | =$ ．

查看试题解析
14. 已知方程 $\frac{x - 2}{5} = 2 - \frac{x + 3}{2}$ 的解也是方程 $| 3 x - 2 | = b$ 的解，则b=.

查看试题解析
15. 如图，O为直线 $A B$ 上一点， $O E$ 、 $O F$ 分别是 $∠ A O C$ 、 $∠ B O C$ 的平分线，则 $∠ A O E$ 的余角是．

查看试题解析
16. 卖鱼的商贩为了估计鱼塘中有多少斤鱼，就用渔网先捞出了20条鱼，总重60斤，并在每条鱼上做了标记，随后仍放入鱼塘，一个小时后，再次捞出了30条鱼，发现其中有3条带有标记．根据此数据，可估计鱼塘中有鱼斤．

查看试题解析

三、解答题

17.

(1)、 $2 x - (x + 10) = 6 x$

(2)、 $1 - \frac{3 x - 5}{2} = \frac{1 + 5 x}{3}$ ．

查看试题解析
18. 已知 $3^{m} = 6$ ， $3^{n} = 2$ ，求 $3^{2 m + n - 1}$ 的值

查看试题解析
19. 先化简 $2 ( x^{2} y + 3 x y^{2}) - 3 ( x^{2} y - 1) - 2 x^{2} y - 2$ ，再求值，其中 $x = - 2$ ， $y = 2$ ．

查看试题解析
20. 为了节约用水，某市规定三口之家每月标准用水量为 $15$ 立方米，超过部分加价收费，假设不超过部分水费为 $1.5$ 元 $/$ 立方米，超过部分水费为 $3$ 元/立方米．

(1)、如果甲、乙两家用水量分别为 $10$ 立方米和 $20$ 立方米，那么甲、乙两家该月应各交多少水费？

(2)、当每月用水量为 $a$ 立方米时，请用代数式分别表示这家按标准用水量和超出标准用水时各应缴纳的水费；

(3)、当丁家本月交水费 $46.5$ 元时，那么丁家该月用水多少立方米？

查看试题解析
21. 某市为鼓励居民节约用水，规定如下用水收费标准：每户每月的用水量不超过12吨（含12吨）时，水费按a元/吨收费；超过时，不超过12吨（含12吨）时，水费按a元/吨收费；超过时，不超过12吨的部分仍按a元/吨收费，超过的部分按b元/吨 $(b > a)$ 收费，已知该市小明家今年3月份和4月份的用水量、水费如表所示：
月份
用水量（立方米）
水费（元）
3
28
56
4
20
35.2

(1)、求a，b的值；

(2)、设某户1个月的用水量为x（吨），应交水费y（元），求出y与x之间的函数关系式；

(3)、已知某户5月份的用水量为18吨，求该户5月份的水费．

查看试题解析
22. 设x，y，z为互不相等的非零实数，且 $x + \frac{1}{y} = y + \frac{1}{z} = z + \frac{1}{x}$ ．求证： $x^{2} y^{2} z^{2} = 1$ ．

查看试题解析
23. 如图，直线AB、CD相交于点O，OM⊥AB.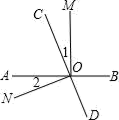

(1)、若∠1=∠2，证明：ON⊥CD；

(2)、若∠1= $\frac{1}{4}$ ∠BOC，求∠BOD的度数.

查看试题解析
24. 我市某校九年级实行小组合作学习，为了解学生课堂发言情况，随机抽取该年级部分学生，对他们每天在课堂上发言的次数进行调查和统计，统计表如下，并绘制了两幅不完整的统计图，已经知A、B两组发言人数直方图高度比为 $1 ： 5$ ．

发言次数n
A
$0 \leq n < 5$
B
$5 \leq n < 10$
C
$10 \leq n < 15$
D
$15 \leq n < 20$
E
$20 \leq n < 25$
F
$25 \leq n < 30$
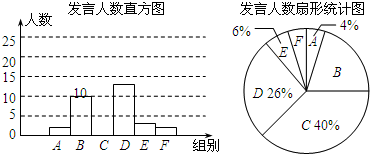
请结合图中相关的数据回答下列问题：

(1)、A组的人数是多少？本次调查的样本容量是多少？

(2)、求出C组的人数并补全直方图；

(3)、该校七年级共有250人，请估计全年级每天在课堂上发言次数不少于15次的人数．

查看试题解析
25. 为响应国家节能减排的号召，鼓励居民节约用电，各省市先后出台了“阶梯价格”制度，如表中是某市的电价标准（每月）
阶梯
电量x（单位：度）
电费价格（单位：元/度）
一档
0＜x≤180
a
二档
180＜x≤400
b
三档
x＞400
0.95

(1)、已知陈女士家三月份用电256度，缴纳电费154.56元，四月份用电318度，缴纳电费195.48元请你根据以上数据，求出表格中的a，b的值．

(2)、5月份开始用电增多，陈女士缴纳电费280元，求陈女士家5月份的用电量．

查看试题解析

	发言次数n
A	$0 \leq n < 5$
B	$5 \leq n < 10$
C	$10 \leq n < 15$
D	$15 \leq n < 20$
E	$20 \leq n < 25$
F	$25 \leq n < 30$

阶梯	电量x（单位：度）	电费价格（单位：元/度）
一档	0＜x≤180	a
二档	180＜x≤400	b
三档	x＞400	0.95

月份	用水量（立方米）	水费（元）
3	28	56
4	20	35.2