浙江省湖州市长兴县2021-2022学年七年级下学期精准教学阶段性综合分析材料（一）数学试题

试卷更新日期：2023-02-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是（）

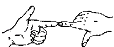A、同位角 B、内错角 C、对顶角 D、同旁内角

查看试题解析
2. 2022年，在中国举办了第二十四届冬季奥林匹克运动会，图中是吉祥物“冰墩墩”，将图中的“冰墩墩”通过平移可以得到的图形是（）

A、 B、 C、 D、

查看试题解析
3. 下面各组数值中，二元一次方程2x+y=10的解是（）

A、 ${\begin{cases} x = - 2 \\ y = 6 \end{cases}$ B、 ${\begin{cases} x = 6 \\ y = - 2 \end{cases}$ C、 ${\begin{cases} x = 4 \\ y = 3 \end{cases}$ D、 ${\begin{cases} x = - 3 \\ y = 4 \end{cases}$

查看试题解析

4. 某同学的作业如下框，其中※处填的依据是（）

如图，已知直线 $l_{1} ， l_{2} ， l_{3} ， l_{4}$ .若 $∠ 1 = ∠ 2$ ，则 $∠ 3 = ∠ 4$ .

请完成下面的说理过程.

解：已知 $∠ 1 = ∠ 2$ ，

根据（内错角相等，两直线平行），得 $l_{1} // l_{2}$ .

再根据（ ※ ），得 $∠ 3 = ∠ 4$ .

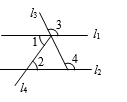A、两直线平行，内错角相等 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，同旁内角互补

查看试题解析

5. 2022年2月6日女足亚洲杯决赛，在逆境中铿锵玫瑰没有放弃，逆转夺冠！某学校掀起一股足球热，举行了班级联赛，某班开局11场保持不败，积23分，按比赛规则，胜一场得3分，平一场得1分，则该班获胜的场数为（）

A、4 B、5 C、6 D、7

查看试题解析
6. 在同一平面内，不重合的三条直线a、b、c中，如果 $a ⊥ b$ ， $b ⊥ c$ ，那么a与c的位置关系是（）

A、垂直 B、平行 C、相交 D、不能确定

查看试题解析
7. 小亮解方程组 ${\begin{matrix} 2 x + y = ▲ \\ 2 x - y = 12 \end{matrix}$ 的解为 ${\begin{matrix} x = 5 \\ y = ☆ \end{matrix}$ ，由于不小心滴上了两滴墨水，刚好遮住了两个数 $▲$ 和 $☆$ ，则这两个数分别为(　　)

A、4和6 B、6和4 C、2和8 D、8和﹣2

查看试题解析
8. 如图，下列四组条件中，能判断 $A B / / C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ A B C + ∠ B C D = 180^{°}$ D、 $∠ B A D + ∠ A B C = 180^{°}$

查看试题解析
9. 《九章算术》是人类科学史上应用数学的“算经之首”，书中记载：今有三人共车，二车空；二人共车，九人步.问：人与车各几何？译文：若3人坐一辆车，则两辆车是空的；若2人坐一辆车，则9人需要步行.问：人与车各多少？设有 $x$ 辆车，人数为 $y$ ，根据题意可列方程组为（）

A、 ${\begin{array}{l} y = 3 x - 2 \\ y = 2 x + 9 \end{array}$ B、 ${\begin{array}{l} y = 3 (x - 2) \\ y = 2 x + 9 \end{array}$ C、 ${\begin{array}{l} y = 3 x - 2 \\ y = 2 x - 9 \end{array}$ D、 ${\begin{array}{l} y = 3 (x - 2) \\ y = 2 x - 9 \end{array}$

查看试题解析
10. 如图，在一个大长方形中放入六个形状、大小相同的小长方形，所标尺寸如图所示，则图中阴影部分的面积是（）

A、16 B、44 C、96 D、140

查看试题解析

二、填空题

11. 已知4x－y=6，用含x的代数式表示y，则y= ．

查看试题解析
12. 如图，把一块三角板的直角的顶点放在直尺的一边上，若 $∠ 1 = 48 °$ ，则 $∠ 2 =$

查看试题解析
13. 如果实数x，y满足方程组 ${\begin{array}{l} x - 2 y = - 1 \\ x + y = 2 \end{array}$ ，那么 $(2 x - y)^{2022} =$ .

查看试题解析
14. 如图所示，一个宽度相等的纸条按如图所示方法折叠一下，则∠1= ．

查看试题解析
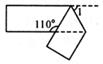15. 一个两位数，个位上的数比十位上的数的2倍多1，若将十位数字与个位数字调换位置，则比原两位数的2倍还多2，则原两位数是．

查看试题解析
16. 一副三角板按如图所示叠放在一起，∠C＝60°，∠OAB＝45°，其中点B、D重合，若固定 $△$ AOB，将三角板ACD绕着公共顶点A顺时针旋转一周后停止，当旋转角为时，CD∥AO.

查看试题解析

三、解答题

17. 阅读并填空：如图，已知 $D E ∥ B C$ ，如果 $∠ A D E = ∠ A E D$ ，那么 $∠ B$ 与 $∠ C$ 相等吗？为什么？
解：因为 $D E ∥ B C$ （已知），
所以 $∠ A D E =$       ▲      .
$∠ A E D = ∠ C$ （            ）.
因为 $∠ A D E = ∠ A E D$ （            ），
所以 $∠ B = ∠ C$ （等量代换）.

查看试题解析
18. 解方程组：

(1)、 ${\begin{cases} 2 x - y = 14 \\ x - 4 y = 0 \end{cases}$

(2)、 ${\begin{cases} \frac{x}{3} - \frac{y}{4} = 1 \\ 3 x - 4 y = 2 \end{cases}$

查看试题解析
19. 如图， $△ A B C$ 沿直线l向右平移 $4 c m$ ，得到 $△ F D E$ ， $B C = 6 c m$ ， $∠ 1 = 45 °$ .

(1)、求 $B E$ 的长；

(2)、求 $∠ 2$ 的度数.

查看试题解析
20. 2022年北京冬奥会期间体育中心举行短道速滑比赛，观看短道速滑比赛的门票分为两种：A种门票600元/张，B种门票120元/张．某旅行社为一个旅行团代购部分门票，若旅行社购买A，B两种门票共15张，总费用5160元，求旅行社为这个旅行团代购的A种门票和B种门票各多少张？

查看试题解析
21. 如图，已知AC∥FE，∠1＋∠2＝180°

(1)、求证：∠FAB＝∠BDC；

(2)、若AC平分∠FAD，EF⊥BE于点E，∠FAD＝80°，求∠BCD的度数．

查看试题解析
22. 已知关于x，y的方程组 ${\begin{array}{l} x - y = 2 a + 1 \\ 2 x + 3 y = 9 a - 8 \end{array}$ ，其中a是常数.

(1)、若 $a = 2$ 时，求这方程组的解：

(2)、若 $x = y$ ，求这方程组的解：

(3)、若方程组的解也是方程 $x - 6 y = 2$ 的一个解，求a的值.

查看试题解析
23. 某一天，蔬菜经营户王大叔花270元从蔬菜批发市场批发了黄瓜和茄子共70千克，到菜市场按零售价卖，黄瓜和茄子当天的批发价和零售价如下表所示：
品名
黄瓜
茄子
批发价/（元/千克）
5
3
零售价/（元/千克）
7
4

(1)、王大叔当天批发了黄瓜和茄子各多少千克？

(2)、他卖完这些黄瓜和茄子共赚了多少元？

查看试题解析
24. （1）【问题】
如图1，若 $A B ∥ C D$ ， $∠ B E P = 25 °$ ， $∠ P F C = 150 °$ ，求 $∠ E P F$ 的度数；（提示：过点P作 $P Q ∥ A B$ ）

(1)、【问题迁移】
如图2， $A B ∥ C D$ ，点P在AB的上方， $∠ P E A$ ， $∠ P F C$ ， $∠ E P F$ 之间有何数量关系？请说明理由；

(2)、【联想拓展】
如图3所示，在（2）的条件下，已知 $∠ E P F = α$ ， $∠ P E A$ 的平分线和 $∠ P F C$ 的平分线交于点G，用含有 $α$ 的式子表示 $∠ G$ 的度数.

查看试题解析

品名	黄瓜	茄子
批发价/（元/千克）	5	3
零售价/（元/千克）	7	4