2022-2023学年浙教版数学七年级下册4.3 用乘法公式分解因式同步练习

试卷更新日期：2023-02-09 类型：同步测试

进入出卷网下载

一、单选题

1. 如果 $x^{2} + k x + \frac{1}{4}$ 是一个完全平方式，则 $k$ 为（）

A、1 B、 $± 1$ C、-1 D、4

查看试题解析
2. 若代数式 $x^{2} + m x + 25$ 通过变形可以写成 ${(x + n)}^{2}$ 的形式，则m的值是（）

A、5 B、10 C、±5 D、±10

查看试题解析
3. 将 $m^{3} n - m n$ 进行因式分解，正确的是（）

A、 $m (m^{2} n - n)$ B、 $m n (m - 1)^{2}$ C、 $m n (m + 1) (m - 1)$ D、 $m n (m^{2} - 1)$

查看试题解析
4. 下列各式中，能用完全平方公式进行因式分解的是（）

A、 $x^{2} - 4 x + 1$ B、 $x^{2} - 4 x + 2$ C、 $x^{2} - 4 x + 4$ D、 $x^{2} - 4 x - 4$

查看试题解析
5. 下列多项式能用平方差公式分解因式的是（）

A、 $a^{2} + (- b)^{2}$ B、 $a^{2} + b^{2}$ C、 $- a^{2} - b^{2}$ D、 $- a^{2} + b^{2}$

查看试题解析
6. 若x²＋2(2p－3)x＋4是完全平方式，则p的值等于（）

A、 $\frac{5}{2}$ B、2 C、2或1 D、 $\frac{5}{2}$ 或 $\frac{1}{2}$

查看试题解析
7. 添加一项，能使多项式 $9 x^{2} + 1$ 构成完全平方式的是（）

A、 $- 6 x$ B、 $- 9 x$ C、 $9 x^{2}$ D、 $9 x$

查看试题解析
8. 下列各多项式中，能运用公式法分解因式的有（）
① $- m^{2} + 4$ ② $- x^{2} - y^{2}$ ③ $x^{2} y^{2} - 1$ ④ ${(m - a)}^{2} - {(m + a)}^{2}$ ⑤ $2 x^{2} - 8 y^{2}$ ⑥ $- x^{2} - 2 xy - y^{2}$ ⑦ $9 a^{2} b^{2} - 3 ab + 1$

A、4个 B、5个 C、6个 D、7个

查看试题解析
9. 下列等式中，从左到右的变形属于因式分解且分解彻底的是（）

A、 $a^{3} + 2 a^{2} + a = a {(a + 1)}^{2}$ B、 $a (a - b) = a^{2} - a b$ C、 $x^{4} - 1 = (x^{2} + 1) (x^{2} - 1)$ D、 $a x^{2} - a b x + a = a (x^{2} - b x) + a$

查看试题解析
10. 已知 $4 x^{2} + 1$ 加上一个单项式后能成为一个整式的完全平方，给出下面四个单项式① $4 x$ ， ② $- 2 x$ ， ③ $-$ 1 ， ④ $4 x^{4}$ ，其中满足条件的共有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 已知 $a^{2} + 2 k a b + 9 b^{2}$ 是一个完全平方式，那么 $k =$ ．

查看试题解析
12. 学完因式分解后，小亮同学总结出了因式分解的流程图，如图，
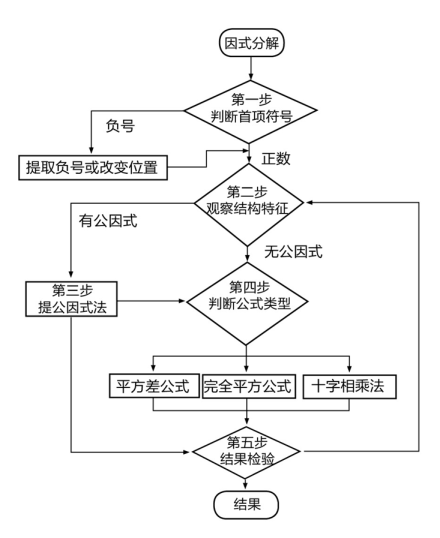
下面是小亮同学的因式分解过程：
$2 x^{2} - 12 x y + 18 y^{2}$
$= 2 (x^{2} - 6 x y + 9 y^{2})$                       ①
$= 2 [x^{2} - 2 \cdot x \cdot 3 y + (3 y)^{2}]$              ②
$=$ ____                                        ③
回答下面的问题：

(1)、①完成了上面流程图的第步；

(2)、②完成了上面流程图的第步；

(3)、将③的结果写在横线上．

查看试题解析
13. 分解因式 $x^{2} (a - b) + 4 y^{2} (b - a) =$

查看试题解析
14. 多项式 $4 a^{2} + 9$ 加上一个单项式后，可化为一个整式的平方，则这个单项式是.（写一个即可）

查看试题解析

三、综合题

15. 因式分解：

(1)、4x²-64

(2)、2x³y+4x²y²+2xy³

查看试题解析
16. 下面是嘉淇同学把多项式 $- 16 m y^{2} + 4 m x^{2}$ 分解因式的具体步骤：
$- 16 m y^{2} + 4 m x^{2}$
利用加法交换律变形：
$= 4 m x^{2} - 16 m y^{2}$
第一步
提取公因式 $m$ ：
$= m (4 x^{2} - 16 y^{2})$
第二步
逆用积的乘方公式
$= m [{(2 x)}^{2} - {(4 y)}^{2}]$
…．第三步
运用平方差公式因式分____ $= m (2 x + 4 y) (2 x - 4 y)$
……第四步

(1)、事实上，嘉淇的解法是错误的，造成错误的原因是；

(2)、请给出这个问题的正确解法．

查看试题解析
17. 阅读理解：
对于二次三项式 $x^{2} + 2 a x + a^{2}$ ，能直接用公式法进行因式分解，得到 $x^{2} + 2 a x + a^{2} = {(x + a)}^{2}$ ，但对于二次三项式 $x^{2} + 2 a x - 8 a^{2}$ ，就不能直接用公式法了.

我们可以求用这样的方法：在二次三项式 $x^{2} +$ $2 a x - 8 a^{2}$ 中先加上一项 $a^{2}$ ，使其成为完全平方式，再减去 $a^{2}$ 这项，使整个式了的值不变，于是：

$x^{2} + 2 a x - 8 a^{2}$

$= x^{2} + 2 a x - 8 a^{2} + a^{2} - a^{2}$

$= x^{2} + 2 a x + a^{2} - 8 a^{2} - a^{2}$

$= (x^{2} + 2 a x + a^{2}) - (8 a^{2} + a^{2})$

$= {(x + a)}^{2} - 9 a^{2}$

$= (x + a + 3 a) (x + a - 3 a)$

$= (x + 4 a) (x - 2 a)$

像这样把二次三项式分解因式的方法叫做添(拆)项法.

(1)、问题解决：请用上述方法将二次三项式x²＋2ax—3a²分解因式；

(2)、拓展应用：二次三项式x²-4x＋5有最小值或最大值吗？如果有，请你求出来并说明理由.

查看试题解析

2022-2023学年浙教版数学七年级下册4.3 用乘法公式分解因式 同步练习

一、单选题

二、填空题

三、综合题

2022-2023学年浙教版数学七年级下册4.3 用乘法公式分解因式同步练习