2023年苏科版数学七年级下册全方位训练卷第七章 平面图形的认识（二）
试卷更新日期：2023-02-08 类型：单元试卷
一、作图题（共2题，共22分）
-
1. 如图，每个小正方形的边长均为1，每个小方格的顶点叫格点.
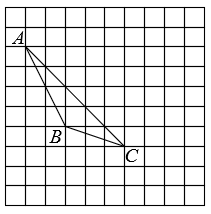(1)、画出格点△ABC中AB边上的中线CD.(2)、画出△ABC向右平移4个单位后，再向上平移3个单位得到的△A1B1C1(3)、图中AC与A1C1的关系是：.(4)、求△ABC的面积.(5)、能使S△ABE＝S△ABC的格点E共有个.2. 如图，在边长为1个单位的正方形网格中，△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B′.根据下列条件，利用网格点和无刻度的直尺画图并解答相关的问题（保留画图痕迹）：
（ 1 ）在给定方格纸中画出平移后的△A'B'C'；
（ 2 ）画出AB边上的中线CD；
（ 3 ）画出BC边上的高线AE；
（ 4 ）△A'B'C'的面积为 ▲ ；
（ 5 ）在图中能使S△PAC＝S△ABC的格点P的个数有 ▲ 个（点P异于点B）.
二、解答题（共11题，共70分）
-
3. 如图，直线a、b被直线c所截， ， 直线a、b平行吗？为什么？
4. 如图，在△ABC中，点D在BC上，且∠BAD＝∠CAD，E是AC的中点，BE交AD于点F．图中哪条线段是哪个三角形的角平分线？哪条线段是哪个三角形的中线？
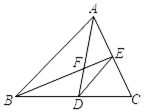5. 根据下列推理进行填空：已知：如图，点 在 上，且 平分 ， .求证： .
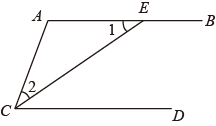
证明：∵ 平分 （已知）
∴ __▲_（ ）
又∵ （ ）
∴ _▲（ ）
∴ （ ）
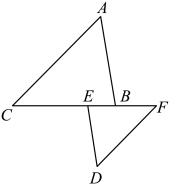
6. 已知：如图，点C、E、B、F在一条直线上， ， ∠A＝∠D．求证： ．
7. 已知一个多边形的内角和比它的外角和的3倍多 ．(1)、求这个多边形是几边形；(2)、如果从这个多边形的一个顶点引出对角线，最多可以引条对角线．8. 如图，△ABC中，∠C＝90° ， AC＝8cm，BC＝6cm，AB＝10cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒3cm，设运动的时间为t秒．
(1)、当t＝时，CP把△ABC的周长分成相等的两部分？(2)、当t＝时，CP把△ABC的面积分成相等的两部分？(3)、当t为何值时，△BCP的面积为18？9. 在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌）．这显然与正多边形的内角大小有关．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．(1)、请根据下列图形，填写表中空格：
正多边形边数
3
4
5
6
…
n
正多边形每个内角的度数
…
(2)、如果只限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？10. 在中，射线平分交于点 ， 点在直线上运动（不与点重合），过点作交直线于点 ．
(1)、如图1，点在线段上运动时，平分 ，①若 ， ， 则 ▲ ；
②若 ， 则 ▲ ；
③探究与之间的数量关系，说明理由；
(2)、若点在射线上运动时，的角平分线所在直线与射线交于点 ， 与之间的数量关系是否与（1）中③相同，若不同请写出新的关系并画图说明理由．11. 如图，直线 ， 点E，G在直线AB上，点F，H在直线CD上，∠1＋∠2＝180°．
(1)、如图1，求证：；(2)、如图2，若∠1＝120°，GM平分∠BGH，FM平分∠EFH，设FM与GH相交于点O．求∠FOH的度数．12. 如图1，将一副三角板中的两个直角顶点叠放在一起，其中 ， ， .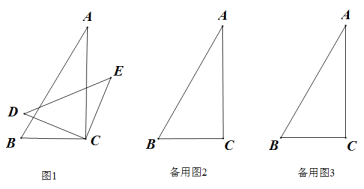
(1)、观察猜想，∠BCD与∠ACE的数量关系是；∠BCE与∠ACD的数量关系是；(2)、类比探究，若按住三角板不动，顺时针绕直角顶点转动三角形 ， 试探究当∠ACD等于多少度时CE//AB，画出图形并简要说明理由；(3)、拓展应用，若∠BCE＝3∠ACD，求∠ACD的度数；并直接写出此时DE与AC的位置关系.13. 如图，∠AOB＝40°，OC平分∠AOB，点D，E在射线OA，OC上，点P是射线OB上的一个动点，连接DP交射线OC于点F，设∠ODP＝x°.
(1)、如图 1，若DE∥OB，∠EDF＝∠EFD，求x的值；(2)、如图 2，若DE⊥OA，是否存在这样的 x 的值，使得∠EFD＝4∠EDF？若存在，求出 x的值；若不存在，说明理由.(3)、在（2）的条件下，若射线DA绕点D顺时针旋转至DO后立即回转，射线EO绕点E顺时针旋转至ED停止，射线DA转动的速度是4°/秒，射线EO转动的速度是1°/秒.若射线DA先旋转4秒，射线EO才开始绕点E顺时针旋转，在射线EO到达ED之前，射线EO旋转到第几秒时，射线DA与射线EO互相平行，直接写出答案.三、单选题（每题2分，共16分）
-
14. 现实世界中，平移现象无处不在，中国的汉字中有些也可通过平移得到，下列汉字可以看成是通过平移构成的是（ ）A、
B、
C、
D、
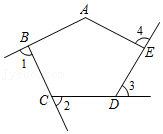
15. 如图，下面哪个条件不能判断EF∥DC的是（ ）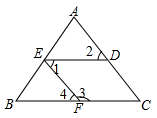
A、∠1＝∠2 B、∠4＝∠C C、∠1+∠3＝180° D、∠3+∠C＝180°16. 如图，下列判断错误的是（ ）
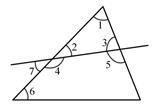A、∠1和∠2是同旁内角 B、∠3和∠4是内错角 C、∠5和∠6是同旁内角 D、∠5和∠7是同位角17. 如图， // 分别交 于点E、F， ，则 的度数是（ ）
A、 B、 C、 D、18. 若一个三角形的三个内角度数的比为2：3：4，则这个三角形是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形19. 如图，AD是△ABC的中线，点E在线段AD上，且 ． 若△DEC的面积是1，则△ABD的面积是（ ）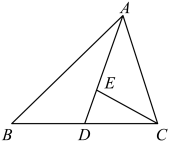
A、2 B、3 C、4 D、620. 如图，张明同学设计了四种正多边形的瓷砖图案，这四种瓷砖图案中，不能铺满地面的是（ ）A、
B、
C、
D、
21. 把一副三角尺按如图所示放置（2个直角顶点重合），则∠1、∠2、∠3的和是（ ）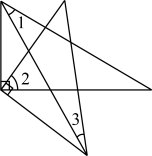
A、60° B、90° C、105° D、120°四、填空题（每题3分，共12分）
-
22. 如图，点在射线上，请你添加一个条件 ， 使得 ．
