2023年苏科版数学七年级下册全方位训练卷7.5多边形的内角和与外角和

试卷更新日期：2023-02-08 类型：同步测试

进入出卷网下载

一、单选题（每题2分，共16分）

1. 一个多边形的内角和的度数可能是（）

A、1700° B、1800° C、1900° D、2000°

查看试题解析
2. 下列平面图形中，内角和是1080°的是（）

A、 B、 C、 D、

查看试题解析
3. 从五边形的一个顶点出发，可以画出m条对角线，它们将五边形分成n个三角形．则m、n的值分别为（）

A、3，2 B、2，2 C、2，3 D、3，3

查看试题解析
4. n边形所有对角线的条数有（）

A、 $\frac{n (n - 1)}{2}$ 条 B、 $\frac{n (n - 2)}{2}$ 条 C、 $\frac{n (n - 3)}{2}$ 条 D、 $\frac{n (n - 4)}{2}$ 条

查看试题解析
5. 在 $△ A B C$ 中， $∠ A = \frac{1}{2} ∠ B = \frac{1}{3} ∠ C$ ，则 $△ A B C$ 为（）三角形．

A、锐角 B、直角 C、钝角 D、等腰

查看试题解析
6. 如图，点D为 $△ A B C$ 的角平分线AE延长线上的一点，过点D作 $D F ⊥ B C$ 于点F，若 $∠ B = 80 °$ ， $∠ C = 50 °$ ，则 $∠ D$ 的度数是（）

A、 $10 °$ B、 $13 °$ C、 $15 °$ D、 $17 °$

查看试题解析
7. 如图摆放着一副三角板，∠B＝∠EDF＝90°，点E在AC上，点D在BC的延长线上， $E F ∥ B C$ ， ∠A＝30°，∠F＝45°，则∠CED的度数为（）

A、15° B、20° C、30° D、45°

查看试题解析
8. 如图， $∠ A = 100 °$ ， ∠B、∠C、∠D、∠E，∠F的关系为（）

A、 $∠ B + ∠ C + ∠ D + ∠ E + ∠ F = 260 °$ B、 $∠ B + ∠ C - ∠ D + ∠ E + ∠ F = 260 °$ C、 $∠ B + ∠ C + ∠ D + ∠ E + ∠ F = 360 °$ D、 $∠ B + ∠ C - ∠ D + ∠ E + ∠ F = 360 °$

查看试题解析

二、填空题（每题2分，共16分）

9. 若多边形的内角和比外角和大540°，则该多边形的边数是．

查看试题解析
10. 若一个正多边形从一个顶点出发，只可以引3条对角线，则它的每个内角是度．

查看试题解析
11. 如果过某多边形的一个顶点的对角线有6条，则该多边形一共有条对角线．

查看试题解析
12. 若某一个顶点与和它不相邻的其他各顶点连接，可将多边形分成七个三角形，则这个多边形是边形

查看试题解析
13. 如图，小明在用量角器度量 $∠ A O B$ 的大小时，将边OB放在0刻度线上，但是顶点O放在中心点的右侧，此时边OA过50°刻度线，则 $∠ A O B$ 50°．（选填“<”，“=”或“>”）

查看试题解析
14. 将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的大小为度．

查看试题解析
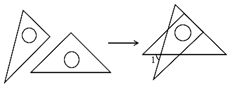15. 一把直尺与一块直角三角板按如图方式摆放，若 $∠ 1 = 47 °$ ，则 $∠ 2 =$ ．

查看试题解析
16. 如图，AE，CE分别平分 $∠ B A D$ 和 $∠ B C D$ ， $∠ B = 32 °$ ， $∠ E = 35 °$ ，则 $∠ D =$ ．

查看试题解析

三、解答题（共10题，共88分）

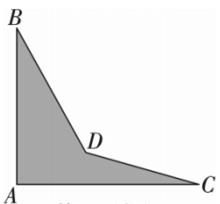
17. 一个多边形的外角和是内角和的 $\frac{2}{5}$ ，求这个多边形的边数及这个多边形共有几条对角线.

查看试题解析
18. 已知一个多边形的每一个内角都比它相邻的外角的4倍多 $30^{\circ}$ ，求这个多边形是几边形?并求出这个多边形的内角和.

查看试题解析
19. 在 $△ A B C$ 中， $A D$ 为边BC上的高， $∠ A B C = 30 °$ ， $∠ C A D = 20 °$ ，求： $∠ B A C$ 的度数．

查看试题解析
20. 一个零件的形状如图所示，按规定， $∠ A = 90^{\circ} ， ∠ B$ 和 $∠ C$ 分别是 $32^{\circ}$ 和 $21^{\circ}$ 的零件为合格零件.现质检工人量得 $∠ B D C = 149^{\circ}$ ，就断定这个零件不合格，请你运用三角形的有关知识说明零件不合格的理由.

查看试题解析
21. 在 $△ A B C$ 中， $∠ B A C = 50 °$ ， $∠ B = 48 °$ ， $A D$ 是 $△ A B C$ 的角平分线，求 $∠ A D C$ 的度数．

查看试题解析
22. 如图，点G，D，E，F在△ABC的边上， $D E ∥ B C$ ， ∠1＝∠2.

(1)、求证： $C D ∥ F G$ ；

(2)、若∠A＝60°，∠B＝50°，CD平分∠ACB，求∠1的大小.

查看试题解析
23.

(1)、分别画出下列各多边形的对角线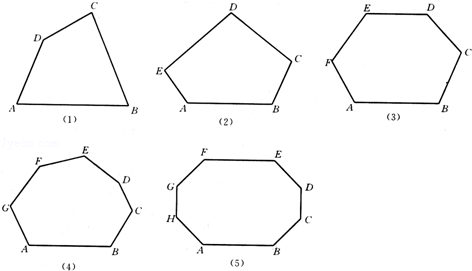

(2)、并观察图形完成下列问题：
①试写出用n边形的边数n表示对角线总条数S的式子：．

②从十五边形的一个顶点可以引出条对角线，十五边形共有条对角线：

③如果一个多边形对角线的条数与它的边数相等，求这个多边形的边数．

查看试题解析
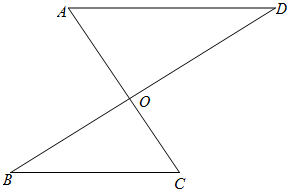
24. 直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．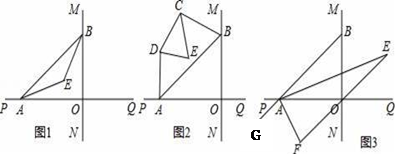

(1)、如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．

(2)、如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．

(3)、如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有两个角度数的比是3：2，请直接写出∠ABO的度数．

查看试题解析
25. 平面内的两条直线有相交和平行两种位置关系， $A B ∥ C D$ 如图，点P在AB、CD外部时，由 $A B ∥ C D$ ，有∠B=∠BOD，因∠BOD+∠POD=180°，∠POD +∠BPD+∠D =180°，故∠BOD=∠BPD +∠D，得∠BPD=∠B-∠D．

(1)、如图，将点P移到AB、CD内部，延长BP交CD于点E，以上结论是否成立？若不成立，则∠BPD、∠B、∠D之间有何数量关系？请说明你的理由；

(2)、如图，直线AB与直线CD交于点Q，延长BP交CD于点F，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需说明理由）；

(3)、若∠A=60°，∠B=15°，∠E=20°，根据（2）的结论求图中∠AGB的度数．

查看试题解析
26. 【概念认识】
如图①，在 $∠ A B C$ 中，若 $∠ A B D = ∠ D B E = ∠ E B C$ ，则BD，BE叫做 $∠ A B C$ 的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．

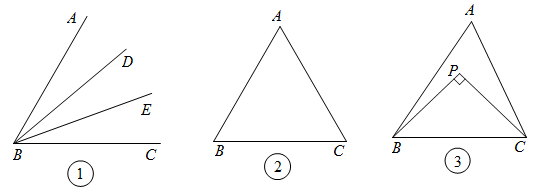
(1)、【问题解决】
如图②，在 $△ A B C$ 中， $∠ A = 70 °$ ， $∠ B = 45 °$ ，若 $∠ B$ 的三分线BD交AC于点D，则 $∠ B D C =$ °；

(2)、如图③，在 $△ A B C$ 中，BP、CP分别是 $∠ A B C$ 邻AB三分线和 $∠ A C B$ 邻AC三分线，且 $B P ⊥ C P$ ，求 $∠ A$ 的度数；

(3)、【延伸推广】
如图，直线AC、BD交于点O， $∠ A D B$ 的三分线所在的直线与 $∠ A C B$ 的三分线所在的直线交于点P．若 $∠ A = 66 °$ ， $∠ B = 45 °$ ， $∠ A D B = m °$ ，直接写出 $∠ D P C$ 的度数．

查看试题解析