2023年苏科版数学七年级下册全方位训练卷7.4认识三角形
试卷更新日期:2023-02-08 类型:同步测试
一、单选题(每题2分,共16分)
-
1. 有下列两种图示均表示三角形分类,则正确的是( )
 A、①对,②不对 B、②对,①不对 C、①、②都不对 D、①、②都对2. 如图,图中的三角形共有( )个.
A、①对,②不对 B、②对,①不对 C、①、②都不对 D、①、②都对2. 如图,图中的三角形共有( )个.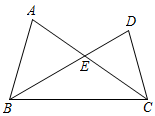 A、 B、 C、 D、3. 下列长度的三条线段中能组成三角形的是( )A、0.1cm,0.1cm,0.1cm B、8cm,8cm,18cm C、3cm,5cm,8cm D、3cm,40cm,8cm4. 三边都不相等的三角形有两边长分别为3和5,第三长是奇数,则其周长为( )A、15 B、13 C、11 D、15或13或115. 在下列各图的中,符合题意画出AC边上高的图形是( )A、
A、 B、 C、 D、3. 下列长度的三条线段中能组成三角形的是( )A、0.1cm,0.1cm,0.1cm B、8cm,8cm,18cm C、3cm,5cm,8cm D、3cm,40cm,8cm4. 三边都不相等的三角形有两边长分别为3和5,第三长是奇数,则其周长为( )A、15 B、13 C、11 D、15或13或115. 在下列各图的中,符合题意画出AC边上高的图形是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,的边上的高是( )
6. 如图,的边上的高是( ) A、 B、 C、 D、7. 在数学实践课上,小亮经研究发现:在如图所示的中,连接点A和BC上的一点D,线段AD等分的面积,则AD是的( ).
A、 B、 C、 D、7. 在数学实践课上,小亮经研究发现:在如图所示的中,连接点A和BC上的一点D,线段AD等分的面积,则AD是的( ). A、高线 B、中线 C、角平分线 D、对角线8. 如图所示,△ABC的面积是2,AD是△ABC的中线,AF=AD,CE=EF,则△CDE的面积为( )
A、高线 B、中线 C、角平分线 D、对角线8. 如图所示,△ABC的面积是2,AD是△ABC的中线,AF=AD,CE=EF,则△CDE的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题2分,共16分)
-
9. 如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出个三角形.
 10. 如图,三角形共有个.
10. 如图,三角形共有个.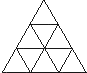 11. 三角形的两边长分别为2cm,5cm,第三边的长xcm也是整数,则当三角形的周长取最大值时,x的值是 .12. 三角形的三边长分别为3, , 5,则的取值范围是 .13. 如图,已知BD是的中线, , , 和的周长的差是 .
11. 三角形的两边长分别为2cm,5cm,第三边的长xcm也是整数,则当三角形的周长取最大值时,x的值是 .12. 三角形的三边长分别为3, , 5,则的取值范围是 .13. 如图,已知BD是的中线, , , 和的周长的差是 . 14. 如图,已知是的中线,点是边上一动点,若的面积为10, , 则的最小值为
14. 如图,已知是的中线,点是边上一动点,若的面积为10, , 则的最小值为 15. 在中,已知点D、E、F分别是边AE、BF、CD上的中点,若的面积是14,则的面积为 .
15. 在中,已知点D、E、F分别是边AE、BF、CD上的中点,若的面积是14,则的面积为 .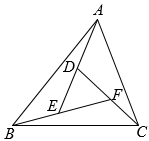 16. 如图,分别为的高和中线,若 , 则的面积为 .
16. 如图,分别为的高和中线,若 , 则的面积为 .
三、作图题(共3题,共27分)
-
17. 图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A、B、C均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写出画法,保留作图痕迹.
 (1)、在图①中,画△ABC的高线AD.(2)、在图②中,画△ABC的中线BE.(3)、在图③中,画△ABF,使△ABF的面积为618. 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.△ABC的顶点都在方格纸格点上.
(1)、在图①中,画△ABC的高线AD.(2)、在图②中,画△ABC的中线BE.(3)、在图③中,画△ABF,使△ABF的面积为618. 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.△ABC的顶点都在方格纸格点上. (1)、请在图中画出ABC先向上平移3个单位,再向左平移2个单位后的△A1B1C1;(2)、图中AC与A1C1的关系是;(3)、图中△ABC的面积是;(4)、请利用三角尺,画出△A1B1C1边B1C1上的高A1D,垂足为点D.19. 我们学过三角形的相关知识,在“信息技术应用”——画图找规律的实践学习中,我们发现了几个基本事实:三角形的三条中线交于一点,三角形的三条角平分线交于一点,三角形的三条高所在的直线交于一点.请根据以上的基本事实,解决下面的问题.
(1)、请在图中画出ABC先向上平移3个单位,再向左平移2个单位后的△A1B1C1;(2)、图中AC与A1C1的关系是;(3)、图中△ABC的面积是;(4)、请利用三角尺,画出△A1B1C1边B1C1上的高A1D,垂足为点D.19. 我们学过三角形的相关知识,在“信息技术应用”——画图找规律的实践学习中,我们发现了几个基本事实:三角形的三条中线交于一点,三角形的三条角平分线交于一点,三角形的三条高所在的直线交于一点.请根据以上的基本事实,解决下面的问题.如图,钝角三角形中, , 分别为 , 边上的高.
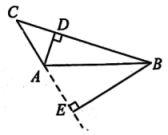 (1)、请用无刻度直尺画出边上的高(保留作图痕迹,不写作法);(2)、在(1)的条件下,若 , , 求高与的比是多少?
(1)、请用无刻度直尺画出边上的高(保留作图痕迹,不写作法);(2)、在(1)的条件下,若 , , 求高与的比是多少?四、综合题(共7题,共61分)
-
20. 已知 是 的三边长,化简 .21. 如图所示,已知△ABC的周长为21 cm,AB=6 cm,BC边上中线AD=5 cm,△ABD的周长为15 cm,求AC的长.
 22. 如图,在△ABC中,AD是角平分线,AE是BC边上的高,∠B=40°,∠C=68°.求∠DAE的度数.
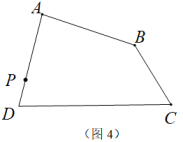
22. 如图,在△ABC中,AD是角平分线,AE是BC边上的高,∠B=40°,∠C=68°.求∠DAE的度数. 23. 如图所示,设四边形 的面积为 ,四边形 的面积为 ,其中E、F分别为 边上的两个三等分点,G、H分别为 边上的两个三等分点,请直接写出 与 的等量关系,并说明理由.
23. 如图所示,设四边形 的面积为 ,四边形 的面积为 ,其中E、F分别为 边上的两个三等分点,G、H分别为 边上的两个三等分点,请直接写出 与 的等量关系,并说明理由. 24. 平面上有三个点A,B,O.点A在点O的北偏东方向上, , 点B在点O的南偏东30°方向上, , 连接AB,点C为线段AB的中点,连接OC.(1)、依题意补全图形(借助量角器、刻度尺画图);(2)、写出的依据:(3)、比较线段OC与AC的长短并说明理由:(4)、直接写出∠AOB的度数.25. 某木材市场上木棒规格与价格如下表:
24. 平面上有三个点A,B,O.点A在点O的北偏东方向上, , 点B在点O的南偏东30°方向上, , 连接AB,点C为线段AB的中点,连接OC.(1)、依题意补全图形(借助量角器、刻度尺画图);(2)、写出的依据:(3)、比较线段OC与AC的长短并说明理由:(4)、直接写出∠AOB的度数.25. 某木材市场上木棒规格与价格如下表:规格
1m
2m
3m
4m
5m
6m
价格(元/根)
10
15
20
25
30
35
小明的爷爷要做一个三角形的木架养鱼用,现有两根长度分别为3m和5m的木棒,还需要到某木材市场上购买一根.
(1)、有几种规格木棒可供小明的爷爷选择?(2)、选择哪一种规格木棒最省钱?26.(1)、【问题提出】在△ABC中,点P是线段BC的中点.在图1中,过点P画一条直线平分△ABC的面积.(2)、【问题探究】育才中学“思维畅想”社团的同学们又研究了这样一个问题:如图2,在△ABC中,点P是线段BC的中点.若点E是线段BP上一点(不与点B、P重合),能否过E作直线平分△ABC的面积?小明给出了如下画法:
作线段AC的中点D;(2)连接DE、BD;(3)过B作BMDE交AC于点M;(4)连接EM,则直线EM平分△ABC的面积.小明画法正确吗?请你说明理由.
(3)、【问题延伸】在四边形ABCD中,点P是AD上一点,请选择图3或图4过点P作直线PQ平分四边形ABCD的面积.