2023年苏科版数学七年级下册全方位训练卷7.3平移的性质
试卷更新日期：2023-02-07 类型：同步测试
一、单选题（每题3分，共24分）
-
1. 下列生活现象中，属于平移的是（ ）A、升降电梯的上下移动 B、荡秋千运动 C、把打开的课本合上 D、钟摆的摆动2. 在如图所示的四个汽车标识图案中，能用平移变换来分析其形成过程的是（ ）A、
B、
C、
D、
3. 下图是某设计师的喀什城标设计作品，图案中总体是由丝绸形成的“喀”字，下列四个图案中，可以通过平移下图图案得到的是（ ）
A、
B、
C、
D、
4. 已知直线 ， ， 互相平行，直线 与 的距离是 ，直线 与 的距离是 ，那么直线 与 的距离是（ ）A、 或 B、 C、 D、5. 如图，将△ABC沿边AC所在直线平移至△EDF处，则下列结论错误的是（ ）
A、BD∥CF B、AE = CF C、∠A = ∠BDE D、AB = EF6. 如图，将△ABC沿BC方向平移1cm得到对应的△A′B′C′．若B′C=2cm，则BC′的长是（ ）
A、2cm B、3cm C、4cm D、5cm7. 如图，把一个三角形纸板的一边紧靠数轴平移，点P平移的距离PP′为（ ）
A、2 B、3 C、4 D、58. 如图，将周长为16的△ABC沿BC方向平移2个单位得到△DEF，则四边形ABFD的周长为（ ）.
A、12 B、16 C、20 D、24二、填空题（每题3分，共24分）
-
9. 下列生活中的物体的运动情况可以看成平移的是 ．
⑴摆动的钟摆；⑵在笔直的公路上行驶的汽车；⑶随风摆动的旗帜；⑷汽车玻璃上雨刷的运动；⑸从楼顶自由落下的球（球不旋转）．
10. 如图，直线 ， 则直线 ， 之间距离是线段的长度．
11. 在同一平面内，设a，b，c是三条互相平行的直线，a与b之间的距离为5，b与c之间的距离是2，则a与c之间的距离是.12. 如图，要在河的两岸搭建一座桥，在PA，PB，PC三种搭建方式中，最短的是PB，其理由是 ．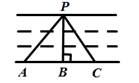
13. 如图，在一块长为30米，宽为16米的长方形草地上，有两条宽都为1米的纵、横相交的小路，这块草地的绿地面积为平方米．
14. 某宾馆重新装修后，准备在大厅的主楼梯上铺设一种红地毯，若这种地毯每平 方米售价40元，主楼梯道宽2米，其侧面如图所示，则买地毯至少需要元，
15. 如图是用三角尺和直尺画平行线的示意图，将三角尺ABC沿着直尺PQ平移到三角尺A'B'C'的位置，就可以画出AB的平行线A'B'．若AC'=9cm，A'C=2 cm，则直线AB平移的距离为cm
16. 如图，将长为6，宽为4的长方形ABCD先向右平移2，再向下平移1，得到长方形A'B'CD'，则阴影部分的面积为 ．
三、作图题（共2题，共16分）
-
17. 如图所示，正方形网格中， 为格点三角形 即三角形的顶点都在格点上 ，每个小正方形的边长都是单位1在网格图中画出 向上平移2个单位，再向右平移4个单位所得的 .
18. 如图，经过平移，四边形ABCD的顶点A移到点A′，作出平移后的四边形．
四、解答题（共8题，共86分）
-
19. 如图所示，某住宅小区内有一块长的长 ，宽 方形形，想在长方形地块内修筑同样宽的两条“之”字路，余下的部分做绿化，道路的宽为 米，求绿化的面积．
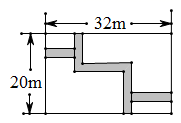20. 如图1，AB、BC被直线AC所截，点D是线段AC上的点，过点D作DE∥AB，连接AE，∠B＝∠E＝75°．
(1)、求证：AE∥BC；(2)、将线段AE沿着直线AC平移得到线段PQ，连接DQ．如图2，当DE⊥DQ时，求∠Q的度数．21. 如图，把直角梯形ABCD沿AD方向平移到梯形EFGH，HG=24cm，WG=8cm，CW=6cm，求阴影部分面积．
22. △ABC在网格中的位置如图所示，请根据下列要求解答：
(1)、过点C作AB的平行线CD，其中要求点D是网格的格点；(2)、A点经平移后到达A1位置，请说明平移过程；(3)、按照（2）的平移过程，作出△ABC经过平移后得到的△A1B1C1；(4)、连结AA1 ， BB1 ， 请直接判断线段AA1与线段BB1的关系．23. 如图，在直角三角形 中， ，将 沿射线 方向平移，得到 ， ， ， 的对应点分别是 ， ， ， .
(1)、请说明 .(2)、若 ，当 时，则 .24. 画图并填空：如图，方格纸中每个小正方形的边长都为1，△ABC的顶点都在方格纸的格点上，将△ABC经过一次平移，使点C移到点C'的位置.
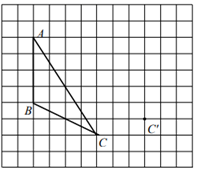(1)、请画出△A'B'C'；(2)、连接AA'、BB'，则这两条线段的关系是；(3)、在方格纸中，画出△ABC的中线BD和高CE；(4)、线段AB在平移过程中扫过区域的面积为.25. 已知点C在射线OA上.
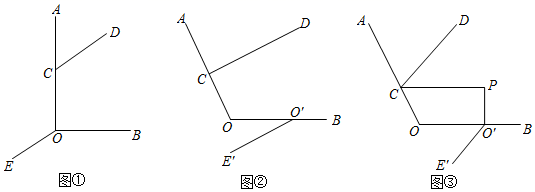(1)、如图①，CD OE，若∠AOB＝90°，∠OCD＝120°，求∠BOE的度数；(2)、在①中，将射线OE沿射线OB平移得O′E'（如图②），若∠AOB＝α，探究∠OCD与∠BO′E′的关系（用含α的代数式表示）(3)、在②中，过点O′作OB的垂线，与∠OCD的平分线交于点P（如图③），若∠CPO′＝90°，探究∠AOB与∠BO′E′的关系.26. 南湖公园有很多的长方形草地，草地里修了很多有趣的小路，下面三个图形都是长为50米，宽为30米的长方形草地，且小路的宽都是1米.
(1)、如图1，阴影部分为1米宽的小路，长方形除去阴影部分后剩余部分为草地，则草地的面积为；(2)、如图2，有两条宽均为1米的小路（图中阴影部分），求草地的面积.(3)、如图3，非阴影部分为1米宽的小路，沿着小路的中间从入口E处走到出口F处，所走的路线（图中虚线）长为.